Short & Long Answer Questions: Oscillations | Physics for Airmen Group X - Airforce X Y / Indian Navy SSR PDF Download
Q.1 Can a motion be periodic and not oscillatory?
Answer: Yes. For example, uniform circular motion is periodic but not oscillatory.
Q.2 Can a motion be oscillatory but not simple harmonic? If your answer is yes, give an example and if not, explain why.
Answer: Yes; when a ball is dropped from a height on a perfectly elastic surface, the motion is oscillatory but not simple harmonic as restoring force F=mg=constant and not F∝−x,which is an essential condition for S.H.M.
Q.3 Every simple harmonic motion is periodic motion, but every periodic motion need not be simple harmonic motion. Do you agree? Give one example to justify your statement.
Answer: Yes, every periodic motion need not be simple harmonic motion. For example, the motion of the earth round the sun is a periodic motion, but not simple harmonic motion as the back and forth motion is not taking place.
Q.4 The rotation of the earth about its axis is periodic but not simple harmonic. Justify.
Answer: The earth takes 24 hours to complete its rotation about its axis, but the concept of to and fro motion is absent, and hence the rotation of the earth is periodic and not simple harmonic.
Q.5 What is the basic condition for the motion of a particle to be S.H.M.?
Answer: The motion of a particle will necessarily be simple harmonic if the restoring force acting on it is proportional to its displacement from the mean position i.e., F=−kx.
Q.6 Which of the following conditions is not sufficient for simple harmonic motion and why? (i) acceleration ∝ displacement, (ii) restoring force ∝ displacement.
Answer: Condition (i) is not sufficient because it does not mention the direction of acceleration. In S.H.M. the acceleration is always in a direction opposite to that of the displacement.
Q.7 Are the functions tan ω t and cotωt periodic? Are they harmonic?
Answer: Both tan ω t and cotωtare periodic functions each with period T=π/ω, because tan 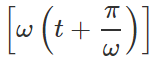 =tan(ωt+π)=tanωt and
=tan(ωt+π)=tanωt and 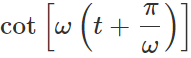 =cot(ωt+π)=cotωt But these functions are not harmonic because they can take any value between 0 and ∞.
=cot(ωt+π)=cotωt But these functions are not harmonic because they can take any value between 0 and ∞.
Q.8 What provides the restoring force for simple harmonic oscillations in the following cases : (i) Simple pendulum (ii) Spring (iii) Column of Hg in U-tube?
Answer: (i) Gravity (ii) Elasticity (iii) Weight of difference column.
Q.9 When are the displacement and velocity in the same direction in S.H.M.?
Answer: When a particle moves from mean position to extreme position, its displacement and velocity are in the same direction.
Q.10 When are the velocity and acceleration in the same direction in S.H.M.?
Answer: When a particle moves from extreme position to mean position, its velocity and acceleration are in the same direction.
Q.11 Can displacement and acceleration be in the same direction in S.H.M.?
Answer: No. In S.H.M., acceleration is always in the opposite direction of displacement.
Q.12 The relation between the acceleration a and displacement x of a particle executing S.H.M. is a=−(p/q)y,where p and q are constants. What will be the time period T of the particle?
Answer: Here  ∴ Time period,
∴ Time period,
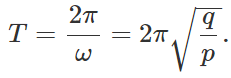
Q.13 The maximum acceleration of a simple harmonic oscillator is a0 and the maximum velocity is υ0. What is the displacement amplitude?
Answer: Let A be the displacement amplitude and co be the angular frequency of S.H.M. Then Maximum velocity, υ0=ωA∴ ω=υ0/A Maximum acceleration, 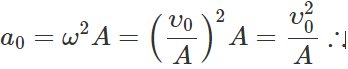 Displacement amplitude,
Displacement amplitude, 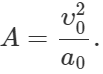
Q.14 The time period of an oscillating body is given by 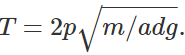 . What would be the force equation for the body?
. What would be the force equation for the body?
Answer: On comparing the given equation 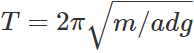 with the standard equation
with the standard equation 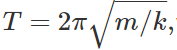 ,we get k=adg,which gives the force equation F=−adg(y).
,we get k=adg,which gives the force equation F=−adg(y).
Q.15 Two simple pendulums of unequal length meet each other at mean position while oscillating. What is their phase difference?
Answer: If both pendulums are moving in the same direction, then ϕ=0∘ and if they are moving in opposite directions, then ϕ=180∘ or π radian.
Q.16 Velocity and displacement of a body executing S.H.M. are out of phase by π/2. How?
Answer: Displacement, x=acosωt Velocity,
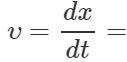 −ωasinωt=ωαcos(ωt+π/2) Clearly, velocity leads the displacement by n π/2 rad.
−ωasinωt=ωαcos(ωt+π/2) Clearly, velocity leads the displacement by n π/2 rad.
Q.17 A particle executes S.H.M. of amplitude A At what positions of its displacement (x), will its (i) velocity be zero and maximum and (ii) acceleration be zero and maximum?
Answer: (i) Zero velocity at x= ±A, maximum velocity at x =0. (ii) Zero acceleration at x= 0,maximum acceleration at x=A.
Q.18 At what points along the path of a simple pendulum is the tension in the string (i) maximum and (ii) minimum?
Answer: (i) The tension is maximum at the mean position and is equal to mg, where m is the mass of the bob. (ii) The tension is minimum at either extreme position and is equal to mg cosθ, where θ is the angle through which the string gets displaced to reach the extreme position.
Q.19 Is the statement "the bob of a simple pendulum moves faster at the lowest position for larger amplitude" true? Justify your answer.
Answer: We know that velocity of a simple pendulum is maximum at the lowest position (mean position) and is given by υmax=ωA. i.e. for larger amplitude (A), the bob of simple pendulum would move faster.
Q.20 Can we use a pendulum watch in an artificial satellite?
Answer: No. In an artificial satellite, a body is in a state of weightlessness, i.e. g= 0.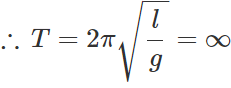 Inside the satellite, the pendulum does not oscillate. Hence a pendulum watch cannot be used in an artificial satellite.
Inside the satellite, the pendulum does not oscillate. Hence a pendulum watch cannot be used in an artificial satellite.
Q.21 A girl is swinging in the sitting position. How will the period of the swing change if she stands up?
Answer: The girl and the swing together constitute a pendulum of time period, 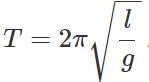 As the girl stands up, her C.G.is raised. The distance between the point of suspension and the C.G.decreases i.e., length l decreases. Hence the time period T decreases.
As the girl stands up, her C.G.is raised. The distance between the point of suspension and the C.G.decreases i.e., length l decreases. Hence the time period T decreases.
Q.22 Will a pendulum clock lose or gain time when taken to the top of a mountain?
Answer: On the top of the mountain, the value of g is less than that on the surface of the earth. The decrease in the value of g increases the time period of the pendulum on the top of the mountain. So the pendulum clock loses time.
Q.23 What will be the period of oscillation, if the length of a second's pendulum is halved?
Answer: 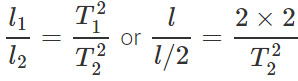 or
or 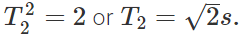
Q.24 The length of second?s pendulum on the surface of earth is 1 m. What will be the length of a second's pendulum on the surface of moon?
Answer: 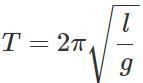 In both the cases, T is same so that l∝g On the moon, the value of acceleration due to gravity is one-sixth of that on the surface of earth. So the length of second?s pendulum is 1/6 m.
In both the cases, T is same so that l∝g On the moon, the value of acceleration due to gravity is one-sixth of that on the surface of earth. So the length of second?s pendulum is 1/6 m.
Q.25 The bob of a simple pendulum is made of wood. What will be the effect on the time period if the wooden bob is replaced by an identical bob of iron?
Answer: There will be no effect because the time period does not depend upon the nature of material of the bob.
Q.26 If a hollow pipe passes across the centre of gravity of the earth, then what changes would take place in the velocity and acceleration of a ball dropped in the pipe?
Answer: The ball will execute S.H.M. to and fro about the centre of the earth. At the centre, the velocity of the ball will be maximum (acceleration zero) and at the earth's surface the velocity will be zero (acceleration maximum).
Q.27 The bob of a simple pendulum of length l is negatively charged. A positively-charged metal plate is placed just below the bob and the pendulum is made to oscillate. What will be the effect on the time - period of the pendulum?
Answer: The positively charged metal plate attracts the negatively charged bob. This increases the effective value of g. Hence the time period will decrease.
Q.28 A simple pendulum of length l and with a bob of mass m is moving along a circular arc of angle θ in a vertical plane. A sphere of mass m is placed at the end of the circle. What momentum will be given to the sphere by the moving bob?
Answer: Zero. This is because the velocity of the bob at the end of the arc will be zero.
Q.29 When a 2.0 kg body is suspended by a spring, the spring is stretched. If the body is pulled down slightly and released, it oscillates up and down. What force is applied on the body by the spring when it passes through the mean position? (g =9.8newton/kg).
Answer: There is no acceleration in the body at the mean position, hence the resultant force applied by the spring will be exactly equal to the weight of the body i.e., 2×9.8 or 19.6 newton.
Q.30 A spring having a force constant k is divided into three equal parts. What would be the force constant for each individual part?
Answer: Force constant of the spring K=F/x, where F is the restoring force. When the spring is divided into three parts, the displacement for the same force reduces to x/3, therefore, the force constant for each individual part is k′=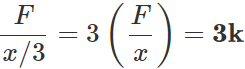
Q.31 How would the time period of a spring mass system change, when it is made to oscillate horizontally, and then vertically?
Answer: Time period will remain the same for both the cases.
Q.32 Alcohol in a U-tube executes S.H.M. of time period T. Now, alcohol is replaced by water up to the same height in the U-tube. What will be the effect on the time period?
Answer: The time period T remains same. This is because the period of oscillation of a liquid in a U-tube does not depend on the density of the liquid.
Q.33 There are two springs, one delicate and another stiffer one. Which spring will have a greater frequency of oscillation for a given load?
Answer: Frequency, 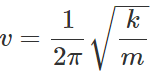 Force constant k is larger for the stiffer spring, so its frequency of oscillation will be greater than that of delicate spring.
Force constant k is larger for the stiffer spring, so its frequency of oscillation will be greater than that of delicate spring.
Q.34 What is the ratio between the potential energy and the total energy of a particle executing S.H.M., when its displacement is half of its amplitude?
Answer: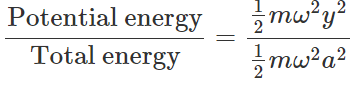
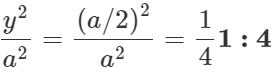
Q.35 What fraction of the total energy is kinetic when the displacement of a simple harmonic oscillator is half of its amplitude?
Answer: 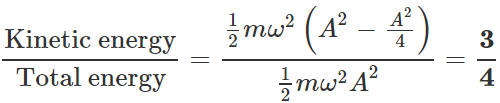
Q.36 Why is restoring force necessary for a body to execute S.H.M.?
Answer: A body in S.H.M. oscillates about its mean position. At the mean position, it possesses kinetic energy because of which it moves from mean position to extreme position. Then the body can return to the mean position only if it is acted upon by a restoring force.
Q.37 What would happen to the motion of the oscillating system if the sign of the force term in the equation F=−kx is changed?
Answer: The force will not be the restoring nature. The back and forth nature of the motion is lost. The body will continue to move in a particular sense.
Q.38 What determines the natural frequency of a body?
Answer: Natural frequency of a body depends upon
(i) elastic properties of the material of the body and
(ii) dimensions of the body.
Q.39 Why does the amplitude of an oscillating pendulum go on decreasing?
Answer: Due to frictional resistance between air and bob, the amplitude of oscillations of the pendulum gradually decreases and finally the bob stops.
Q.40 Why are army troops not allowed to march in steps while crossing a bridge?
Answer: Army troops are not allowed to march in steps while crossing a bridge because it is quite likely that the frequency of the foot steps may match with the natural frequency of the bridge, and due to resonance the bridge may pick up large amplitude and break.
Q.41 A passing aeroplane sometimes causes the rattling of the windows of a house. Why?
Answer: When the frequency of the sound waves from the engine of an aeroplane matches with the natural frequency of a window, resonance takes place which causes the rattling of window.
Q.42 How can earthquakes cause disaster sometimes?
Answer: The resonance may cause disaster during the earthquake, if the frequency of oscillations present within the earth per chance coincides with the natural frequency of some building, which may start vibrating with large amplitude due to resonance and may get damaged.
Q.43 Sometimes a wine glass is broken by the powerful voice of a celebrated singer. Why?
Answer: When the natural frequency of the wine glass becomes equal to that of the singer's voice, the resulting resonance due to the powerful voice of the singer may break the glass.
Q.44 Glass windows may be broken by a far away explosion. Explain why.
Answer: A distant explosion sends out sound waves of large amplitude in all directions. As these sound waves strike the glass windows, they set them into forced oscillations. Since glass is brittle, so the glass windows break as soon as they start oscillating due to forced oscillations.
Q.45 The body of a bus begins to rattle sometimes, when the bus picks up a certain speed. Why?
Answer: At a particular speed, the frequency of the engine of the bus becomes equal to the natural frequency of the body of the bus. The frame of the bus begins to vibrate strongly due to resonance.
Q.46 What will be the change in time period of a loaded spring, when taken to moon?
Answer: Time period of a loaded spring, 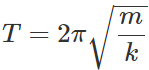 As T is independent of g, it will not be affected when the loaded spring is taken to the moon.
As T is independent of g, it will not be affected when the loaded spring is taken to the moon.
Q.47 A spring of force constant k is cut into two pieces, such that one piece is double the length of the other. What is the force constant of the longer piece of the spring?
Answer: Force constant, k= F/x The length of longer part is 2x /3. So its force constant is 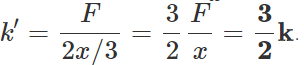
Q.48 In forced oscillation of a particle, the amplitude is maximum for a frequency ω1 of the force, while the energy is maximum for a frequency ω2 of the force. What is relation between ω1 and ω2?
Answer: Only in case of resonance, both amplitude and energy of oscillation are maximum. In the condition of resonance, ω1=ω2.
Q.49 The maximum velocity of a particle, executing simple harmonic motion with an amplitude of 7 mm, is 4.4ms−1. What is the period of oscillation?
Answer: 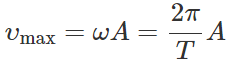
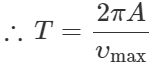
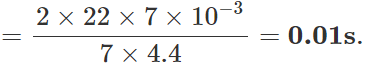
Q.50 Justify the following statements : (i) The motion of an artificial satellite around the earth cannot be taken as S.H.M. (ii) The time period of a simple pendulum will get doubled if its length is increased four times.
Answer: (i) The motion of an artificial satellite around the earth is periodic as it repeats after a regular interval of time. But it cannot be taken as S.H.M. because it is not a to-and-fro motion about any mean position. (ii) Time period of simple pendulum, 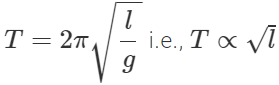 Clearly, if the length is increased four times, the time period gets doubled.
Clearly, if the length is increased four times, the time period gets doubled.
Q.51 (i) What is meant by simple harmonic motion (S.H.M.)? (ii) At what points is the energy entirely kinetic and potential in S.H.M.? (iii) What is the total distance travelled by a body executing S.H.M. in a time equal to its time period, if its amplitude is A?
Answer: (i) Simple harmonic motion. A particle is said to execute simple harmonic motion if it moves to and fro about a mean position under the action of a restoring force which is directly proportional to its displacement from the mean position and is always directed towards the mean position. If the displacement of the oscillating particle from the mean position is small, then Restoring force ∝ Displacement or F∝x or F=−kx where k is positive constant called force constant or spring factor and is defined as the restoring force produced per unit displacement. The negative sign shows that the restoring force always acts in the opposite direction of displacement x. The above equation defines SHM. (ii) The energy is entirely kinetic at mean position i.e., at y=0. The energy is entirely potential at extreme positions, i.e., y=±A. (iii) Total distance travelled in time period T =2A+2A=4A.
Q.52 A simple pendulum consisting of an inextensible length l and mass m is oscillating in a stationary lift. The lift then accelerates upwards with a constant acceleration of 4.5 m/s2. Write expression for the time period of simple pendulum in two cases. Does the time period increase, decrease or remain the same, when lift is accelerated upwards?
Answer: When the lift is stationary T= When the lift accelerates upwards with an acceleration of 4.5 m/s2, T′=2π
When the lift accelerates upwards with an acceleration of 4.5 m/s2, T′=2π 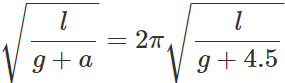 Clearly, the time period decreases when the lift accelerates upwards.
Clearly, the time period decreases when the lift accelerates upwards.
Q.53 What is meant by restoring force? Give one example.
Answer: The force which tends to bring a vibrating body from its displaced position to the equilibrium position is called restoring force. When the bob of a simple pendulum is displaced through an θ from the vertical, a restoring force equal to mg sinθ due to gravity acts on it.
Q.54 The bob of a vibrating pendulum is made of ice. How will the time period change when the ice starts melting?
Answer: If the ice bob is of very small size, the position of its C.G. will remain same as the ice melts. Hence its time period will remain same. If the size of the ice bob is large, then 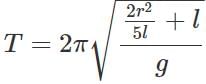 As ice melts, the radius r and hence the time period T will decrease. The pendulum will oscillate faster.
As ice melts, the radius r and hence the time period T will decrease. The pendulum will oscillate faster.
Q.55 The amplitude of a simple harmonic oscillator is doubled. How does this affect (i) periodic time, (ii) maximum velocity, (iii) maximum acceleration and (iv) maximum energy?
Answer: As the acceleration per unit displacement is a constant quantity, T is not affected on changing the amplitude. (ii) υmax=ωA When amplitude is doubled, maximum velocity is also doubled. (iii) amax=ω2A When amplitude is doubled, the maximum acceleration is also doubled. (iv) E=2π2mv2A2 i.e., E∝A2 When amplitude is doubled, the energy of the oscillator becomes four times.
As the acceleration per unit displacement is a constant quantity, T is not affected on changing the amplitude. (ii) υmax=ωA When amplitude is doubled, maximum velocity is also doubled. (iii) amax=ω2A When amplitude is doubled, the maximum acceleration is also doubled. (iv) E=2π2mv2A2 i.e., E∝A2 When amplitude is doubled, the energy of the oscillator becomes four times.
Q.56 You have a light spring, a metre scale and a known mass. How will you find the time period of oscillation of mass without the use of a clock?
Answer: Suspend the known mass m form the spring and note the extension l of the spring with the metre scale. If k is the force constant of the spring, then in equilibrium 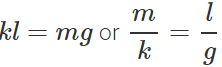 Time period of the loaded spring,
Time period of the loaded spring,
 So by knowing the value of extension l, time period T can be determined.
So by knowing the value of extension l, time period T can be determined.
Q.57 A man is standing on a platform which oscillates up and down simple harmonically. How will the weight of the man change as recorded by a weighing machine on the platform?
Answer: As the platform moves from the mean position to the upper extreme position or from upper extreme position to mean position, the acceleration of the oscillating system acts vertically downwards and hence weight of the man will decrease. On the other hand, as the platform moves from mean position to lower extreme position and then back to mean position, the acceleration acts vertically upwards. Hence weight of the man increases.
Q.58 The frequency of oscillations of a mass m suspended by a spring is v1. If the length of the spring is cut to one-half, the same mass oscillates with frequency v2. Determine the value of v2/v1.
Answer: Let k be the force constant of the full spring Then frequency of oscillation of mass m will be 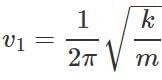 When the spring is cut to one-half of its length, its force constant is doubled (2k). Frequency of oscillation of mass m will be
When the spring is cut to one-half of its length, its force constant is doubled (2k). Frequency of oscillation of mass m will be
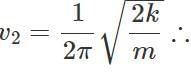 v2/v1=√2
v2/v1=√2
Q.59 All trigonometric functions are periodic, but only sine or cosine functions are used to define S.H.M. Why?
Answer: All trigonometric functions are periodic. The sine and cosine functions can take value between 1 and + 1 only. So they can be used to represent a bounded motion like S.H.M. But the functions such as tangent, cotangent, secant and cosecant can take value between 0 and ∞ (both positive and negative). So those functions cannot be used to represent bounded motion like S.H.M.
Q.60 The length of a simple pendulum executing SHM is increased by 21%. What is the percentage increase in the time period of the pendulum of increased length.
Answer: Time period, 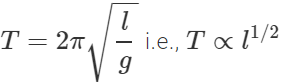 The percentage increase in time period is given by Undefined control sequence \Tau =1/2 × 21
The percentage increase in time period is given by Undefined control sequence \Tau =1/2 × 21
|
201 videos|410 docs|280 tests
|
FAQs on Short & Long Answer Questions: Oscillations - Physics for Airmen Group X - Airforce X Y / Indian Navy SSR
| 1. What are oscillations? |  |
| 2. What is the period of an oscillation? |  |
| 3. What factors affect the period of an oscillation? |  |
| 4. How is the frequency of an oscillation related to its period? |  |
| 5. Can you provide examples of oscillatory motion in everyday life? |  |






















