Class 10 Maths Chapter 2 Question Answers - Polynomials - 2
Ques 21: Find the zeroes of the quadratic polynomial 5x2 - 4 - 8x and verify the relationship between the zeroes and the coefficients of the polynomial.
Sol: p (x) = 5x2 - 4 - 8x
= 5x2 - 8x - 4
= 5x2 - 10x + 2x - 4
= 5x (x - 2) + 2 (x - 2)
= (x - 2) (5x + 2)
∴ zeroes of p (x) are 2 and 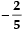
Relationship Verification
Sum of the zeroes 
⇒ 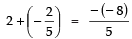
⇒ 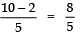
⇒ 8/5 = 8/5
i.e., L.H.S. = R.H.S. ⇒ relationship is verified.
Product of the zeroes = 
⇒ 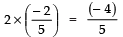
⇒ 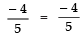
i.e., L.H.S. = R.H.S.
⇒ The relationship is verified.
Ques 22: Find the quadratic polynomial, the sum of whose zeroes is 8 and their product is 12. Hence, find the zeroes of the polynomial.
Sol: ∵ The quadratic polynomial p (x) is given by
x2 - (Sum of the zeroes) x + (Product of the zeroes)
∴ The required polynomial is
= x2 - [8] x + [12]
= x2 - 8x + 12
To find zeroes:
∵ x2 - 8x + 12 = x2 - 6x - 2x + 12
= x (x - 6) - 2 (x - 6)
= (x - 6) (x - 2)
∴ The zeroes of p (x) are 6 and 2.
Ques 23: If one zero of the polynomial (a2 - 9) x2 + 13x + 6a is reciprocal of the other, find the value of ‘a’.
Sol: Here, p (x) = (a2 - 9) x2 + 13x + 6a
Comparing it with Ax2 + Bx + C, we have:
A = (a2 - 9); B = 13; C = 6
Let one of the zeroes = a
∴ The other zero = 1/α
Now, Product of the zeroes 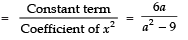
⇒ 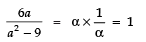
⇒ 6a = a2 − 9 ⇒ a2 − 6a + 9 = 0
⇒ (a − 3)2 =0 ⇒ a − 3=0
⇒ a = 3
Thus, the required value of a is 3.
Ques 24: If the product of zeroes of the polynomial ax2 - 6x - 6 is 4, find the value of ‘a’
Sol: Here, p (x) = ax2 - 6x - 6
∵ Product of zeroes = 
but product of zeroes is given as 4
∴ 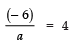 ⇒ − 6 = 4 × a
⇒ − 6 = 4 × a
⇒ 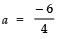 ⇒
⇒ 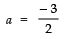
Thus, the required value of a is -3/2.
Ques 25: Find all the zeroes of the polynomial x4 + x3 - 34x2 - 4x + 120, if two of its zeroes are 2 and - 2.
Sol: Here p (x) = x4 + x3 - 34x2 - 4x + 120
∵ The two zeroes of p (x) are 2 and - 2
∴ (x - 2) and (x + 2) are factors of p (x)
⇒ (x - 2) (x + 2) is a factor of p (x)
⇒ x2 - 4 is a factor of p (x).
Now, dividing p(x) by x2 - 4, we have:
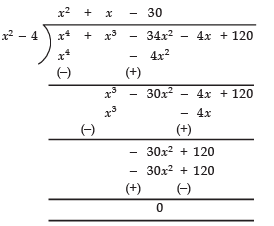
∵ Remainder = 0
∴ p (x) = (x2 - 4) (x2 + x - 30)
i.e., x2 + x - 30 is also a factor of p (x).
∵ x2 + x - 30 = x2 + 6x - 5x - 30 = x (x + 6) - 5 (x + 6)
= (x + 6) (x - 5) = [x - (- 6)] [x - 5]
- 6 and 5 are also zeroes of p (x).
⇒ All the zeroes of the given polynomial are : 2, - 2, 5 and - 6
Ques 26: Find all the zeroes of the polynomial 2x4 + 7x3 - 19x2 - 14x + 30, if two of its zeroes are √2 and -√2.
Sol: P(x) = 2x4 + 7x3 - 19x2 - 14x + 30
∵ √2 and -√2 are the two zeroes of p (x).
∴ 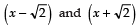 are the factors of p (x).
are the factors of p (x).
⇒ 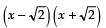 i.e., x2 - 2 is a factor of p (x).
i.e., x2 - 2 is a factor of p (x).
Now, dividing p (x) by x2 - 2, we have:
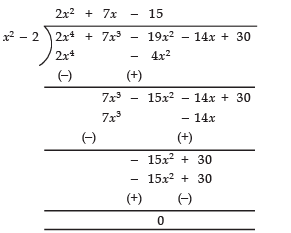
∴ p (x) = (2x2 + 7x - 15) (x2 - 2)
[∵ Remainder = 0]
⇒ 2x2 + 7x - 15 is a factor of p (x)
∵ 2x2 + 7x - 15 = 2x2 + 10x - 3x - 15
= 2x (x + 5) - 3 (x + 5)
= (2x - 3) (x + 5)
= 
∴ 3/2 and - 5 are zeroes of p (x)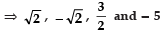 are the zeroes of p (x).
are the zeroes of p (x).
Ques 27: Find the quadratic polynomial whose zeroes are 1 and - 3. Verify the relation between the coefficients and the zeroes of the polynomial.
Sol: ∵ The given zeroes are 1 and - 3.
∴ Sum of the zeroes = 1 + (- 3) = - 2
Product of the zeroes = 1 × (- 3) = - 3
A quadratic polynomial p (x) is given by
x2 - (sum of the zeroes) x + (product of the zeroes)
∴ The required polynomial is
x2 - (- 2) x + (- 3)
⇒ x2 + 2x - 3
Verification of relationship
∵ Sum of the zeroes 
∴ 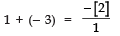
⇒− 2= − 2
i.e., L.H.S = R.H.S ⇒ The sum of zeroes is verified
∵ Product of the zeroes = 
∴ 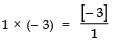
⇒− 3= − 3
i.e., L.H.S = R.H.S ⇒ The product of zeroes is verified.
Ques 28: Find the zeroes of the quadratic polynomial 4x2 - 4x - 3 and verify the relation between the zeroes and its coefficients.
Sol: Here, p (x) = 4x2 - 4x - 3 = 4x2 - 6x + 2x - 3
= 2x (2x - 3) + 1 (2x - 3)
= (2x - 3) (2x + 1)
= 
∴ 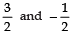 are zeroes of p (x).
are zeroes of p (x).
Verification of relationship
∵ Sum of the zeroes = 
∴ 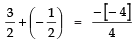
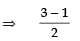
⇒ 2/2 = 1 ⇒ 1= 1
⇒ 
2/2 = 1 ⇒ 1 = 1
i.e., L.H.S = R.H.S ⇒ Sum of zeroes is verified
Now, Product of zeroes = 
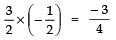
⇒ 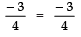
i.e., L.H.S = R.H.S ⇒ Product of zeroes is verified.
Ques 29: Obtain all other zeroes of the polynomial 2x3 - 4x - x2 + 2, if two of its zeroes are √2 and -√2.
Sol: p (x) = 2x3 - 4x - x2 + 2
∵ √2 and -√2 are the zeroes of p (x)
∴  and are the factors of p (x)
and are the factors of p (x)
⇒ 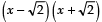 is a factor of p (x)
is a factor of p (x)
⇒ x2 - 2 is a factor of p (x)
Now, Dividing p (x) by (x2 - 2), we have: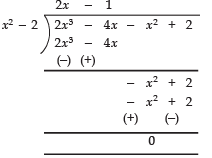
⇒ p (x) = (x2 - 2) (2x - 1)
∴ 2x - 1 is also a factor of p (x)
i.e., is another factor of px.
is another factor of px.
⇒ 1/2 is another zero of p (x)
Ques 30: Find all the zeroes of x4 - 3x3 + 6x - 4, if two of its zeroes are √2 and - √2.
Sol: p (x) = x4 - 3x3 + 6x - 4
∵ √2 and (- √2) are the zeroes of p(x)
∴ x-√2 and x-(- √2) are factors of p (x)
⇒  is a factor of p (x).
is a factor of p (x).
⇒ x2 - 2 is a factor of p (x)
On Dividing p (x) by x2 - 2, we have:
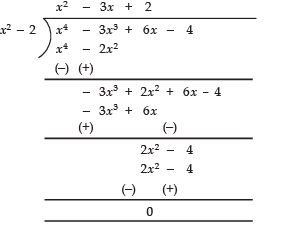
Since, remainder = 0
∴ (x2 - 2) (x2 - 3x + 2) = p (x)
Now, x2 - 3x + 2 = x2 - 2x - x + 2
= x (x - 2) - 1 (x - 2) = (x - 1) (x - 2)
i.e., (x - 1) (x - 2) is a factor of p (x)
∴ 1 and 2 are zeroes of p (x).
∴ All the zeroes of p (x) are ,√2 , - √2, 1 and 2.
Ques 31: Find a quadratic polynomial whose zeroes are - 4 and 3 and verify the relationship between the zeroes and the coefficients.
Sol: We know that:
P (x) = x2 - [Sum of the zeroes] x + [Product of the zeroes] ...(1)
∵ The given zeroes are - 4 and 3
∴ Sum of the zeroes = (- 4) + 3 = - 1
Product of the zeroes = (- 4) × 3 = - 12
From (1), we have
x2 - (- 1) x + (- 12)
= x2 + x - 12 ...(2)
Comparing (2) with ax2 + bx + c, we have
a = 1, b = 1, c = - 12
∴ Sum of the zeroes = -b/a
⇒ (+ 3) + (- 4) = -1/1
i.e., L.H.S = R.H.S ⇒ Sum of zeroes is verified.
Product of zeroes = c/a
⇒ 3 × (- 4) = -12/1
⇒ - 12 = - 12
i.e., L.H.S = R.H.S ⇒ Product of roots is verified.
Ques 32: Using division algorithm, find the quotient and remainder on dividing f (x) by g (x), where f (x) = 6x3 + 13x2 + x - 2 and g (x) = 2x + 1
Sol: Here, f (x) = 6x3 + 13x2 + x - 2
g (x) = 2x + 1
Now, dividing f (x) by g (x), we have:
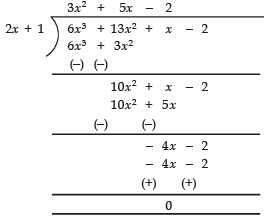
Thus, The quotient = 3x2 + 5x - 2
remainder = 0
Ques 33: If the polynomial 6x4 + 8x3 + 17x2 + 21x + 7 is divided by another polynomial 3x2 + 4x + 1 then the remainder comes out to be ax + b, find ‘a’ and ‘b’.
Sol: We have:
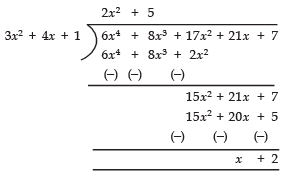
∴ Remainder = x + 2
Comparing x + 2 with ax + b, we have
a = 1 and b = 2
Thus, the required value of a = 1 and b = 2.
Ques 34: If the polynomial x4 + 2x3 + 8x2 + 12x + 18 is divided by another polynomial x2 + 5, the remainder comes out to be px + q. Find the values of p and q.
Sol: We have: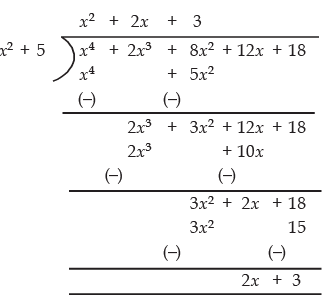
∴ Remainder = 2x + 3
Comparing 2x + 3 with px + q, we have
p = 2 and q = 3
Ques 35: Find all the zeroes of the polynomial x3 + 3x2 - 2x - 6, if two of its zeroes are - √2 and √2.
Sol: p (x) = x3 + 3x2 - 2x - 6
∵ Two of its zeroes are -√2 and √2
⇒  is a factor of p (x)
is a factor of p (x)
⇒ x2 - 2 is a factor of p (x).
Now, dividing p (x) by x2 - 2 we have: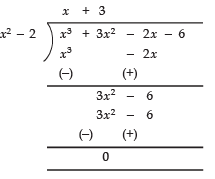
∴ p (x) = (x2 - 2) (x + 3)
i.e., (x + 3) is a factor of p (x),
⇒ (- 3) is a zero of p (x)
∴All the zeroes of p (x) are - √2, √2 and - 3.
Ques 36: Find all the zeroes of the polynomial 2x3 + x2 - 6x - 3, if two of its zeroes are -√3 and √3.
Sol: p (x) = 2x3 + x2 - 6x - 3
Two of its zeroes are -√3 and √3
∴  and are factors of p (x)
and are factors of p (x)
i.e.,  is a factor of p (x)
is a factor of p (x)
⇒ x2 - 3 is a factor of p (x)
Now, Dividing p (x) by x2 - 3, we have: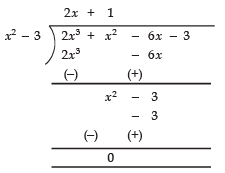
∴ p (x) = (x2 - 3) (2x + 1)
⇒  is a factor of p (x)
is a factor of p (x)
⇒ -1/2 is a zero of p (x)
∴ All the zeroes of p (x) are -√3 , √3 and -1/2.
Ques 37: Find the zeroes of the polynomial 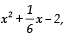 and verify the relation between the coefficients and the zeroes of the above polynomial.
and verify the relation between the coefficients and the zeroes of the above polynomial.
Sol: The given polynomial is
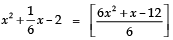
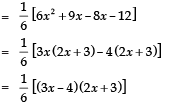
∴ zeroes of the given polynomial are 
Now in, 
co-efficient of x2 = 1
co-efficient of x = 1/6
constant term = –2
∴ Sum of zeroes 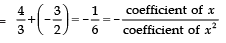
Product of zeroes 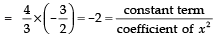
Ques 38: Find the quadratic polynomial, the sum and product of whose zeroes are 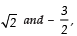 respectively. Also find its zeroes.
respectively. Also find its zeroes.
Sol: Sum of zeroes = √2
Product of zeroes 
∵ A quadratic polynomial is given by
x2 – [sum of roots] x + [Product of roots]
∴ The required polynomial is 
⇒
Since = 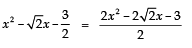
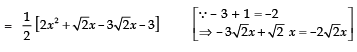
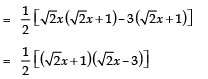
⇒ zeroes are 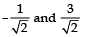
Ques 39: If the remainder on division of x3 + 2x2 + kx + 3 by x - 3 is 21, then find the quotient and the value of k. Hence, find the zeroes of the cubic polynomial x3 + 2x2 + kx - 18.
Sol: Let x3 + 2x2 + kx + 3 = p(x)
∵ The divisor = x – 3
∴ p(3) = 33 + 2 × 32 + 3k + 3
21 = 27 + 18 + 3k + 3
[∵ Remainder = 21]
⇒ 21 – 18 – 3 – 27 = 3k
⇒ –27 = 3k ⇒ k = – 9
Now, the given cubic polynomial
= x3 + 2x2 – 9x + 3
since,
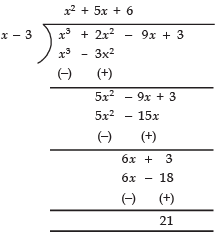
∴ The required quotient = x2 + 5x + 6
Now, x3 + 2x2 – 9x – 18 = (x – 3) (x2 + 5x + 6)
= (x – 3) (x + 3) (x + 2)
⇒ The zeroes of x3 + 2x2 – 9x – 18 are 3, –3 and – 2
Ques 40: If a and b are zeroes of the quadratic polynomial x2 – 6x + a; find the value of ‘a’ if 3α + 2β = 20.
Sol: We have quadratic polynomial = x2 – 6x + a ...(1)
∵ a and b are zeroes of (1)
∴ 

It is given that: 3α + 2β = 20 ...(2)
Now, α +β = 6 ⇒ 2 (α+ β) = 2(6)
2α + 2β = 12 ...(3)
Subtracting (3) from (2), we have
Substituting a = 8 in α + β= 6, we get
8 +β = 6 ⇒ β = –2
Since, αβ = a
8(–2) = α ⇒ α = –16
|
13 videos|79 docs|29 tests
|
FAQs on Class 10 Maths Chapter 2 Question Answers - Polynomials - 2
| 1. What is a polynomial? |  |
| 2. How do you identify the degree of a polynomial? |  |
| 3. Can a polynomial have negative exponents? |  |
| 4. How do you add or subtract polynomials? |  |
| 5. Can a polynomial have more than one variable? |  |
|
13 videos|79 docs|29 tests
|

|
Explore Courses for Class 9 exam
|

|


















