Class 9 Maths Chapter 11 Question Answers - Surface Areas and Volumes
Q1. If the circumference of the base of a right circular cylinder is 110 cm, then find its base area.
Solution: Let r be the radius of the base of the cylinder.
∴ Circumference = 2πr = 2 x(22/7)x r
Now, 2 x(22/7) x r= 110
⇒
Now, Base area =
Q2. The radii of two cylinders are in the ratio of 2 : 3 and heights are in the ratio of 5 : 3.
Find the ratio of their volumes.
Solution: Ratio of the radii = 2 : 3 Let the radii be 2r and 3r Also, their heights are in the ratio of 5:3 Let the height be 5h and 3h
∴ Ratio of their volumes =
Q3. If the radius of a sphere is doubled, then find the ratio of their volumes.
Solution: Let the radius of the original sphere = r
∴ Radius of new sphere = 2r
∴ Ratio of their volumes = = 1/8
Q4. If the radius of a sphere is such that πr2 = 6cm2 then find its total surface area.
Solution: ∵ πr2 = 6cm2
∴ Curved S.A. of the hemisphere
= 2 × 6 cm2 = 12 cm2
Also, plane S.A. of the hemisphere = π r2 = 6 cm2
⇒ Total S.A. = C.S.A. + plane S.A. = 12 cm2 + 6 cm2 = 18 cm2
Q5. The surface area of a sphere of radius 5 cm is five times the area of the curved surface of a cone of radius 4 cm. Find the height and the volume of the cone (taking π = (22/7).
Solution: Surface area of the sphere = 4πr2 = 4 × π × 5 × 5 cm2
Curved surface area of the cone (with slant height as ‘ℓ’) = πrℓ = π × 4 × ℓ cm2
Since,
∴ 4 × π × 5 × 5 = 5 × π × 4 × ℓ
⇒
∴ Volume of the cone =
Q6. Find the slant height of a cone whose radius is 7 cm and height is 24 cm.
Solution: Here, h = 24 cm and r = 7 cm
Since,
= 25 cm
∴ Slant height = 25 cm.
Q7. The diameter of a road roller, 120 cm long is 84 cm. If it takes 500 complete revolutions to level a playground, find the cost of levelling it at ₹2 per square metre.
Solution: Here, radius (r) = 42 cm
Length of the roller = Height of the cylinder
⇒ h = 120 cm
∴ Curved surface area of the roller = 2πrh =2 x(22/7) x 42 x 120 cm2
= 2 x 22 x 6 x 120 cm2 = 31680 cm2
∴ Area levelled in one revolution = 31680 cm2
⇒ Area levelled in 500 revolutions = 31680 x 500 cm2
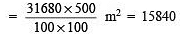
∴ Cost of levelling the playground = 2 x 1584 =
3168.
Q8. A conical tent of radius 7 m and height 24 m is to be made. Find the cost of the 5 m wide cloth required at the rate of 50 per metre.
Solution: Radius of the base of the tent (r) = 7 m
Height (h) = 24 m
Slant height (ℓ)=
Now, curved surface area of the conical tent = πrℓ
= (22/7) x 7 x 25 m2 = 22 x 25 m2 = 550 m2
Let ‘ℓ’ be the length of the cloth.
∴ ℓ x b = 550
⇒ ℓ x 5 = 550
⇒ ℓ = (550/5) m = 110 m
∴ Cost of the cloth = 50 x 110 =
5500.
Q9. How many lead balls, each of radius 1 cm, can be made from a sphere of radius 8 cm?
Solution: Radius of the lead ball (r) = 1 cm
∴ Volume of a lead ball = x 1 x 1 x 1 cm3
= (4/3) x (22/7) cm3
Radius of the sphere (r) = 8 cm
∴ Volume of a sphere = x 8 x 8 x 8 cm3
Let the required number of balls = n
∴ [Volume of n-lead balls] = [Volume of the sphere]
Thus, the required number of balls is 512.
Q10. A particular plastic box 1.5 m long, 1.25 m wide and 65 cm deep are to be made. It is opened at the top. Ignoring the estimated thickness of the plastic sheet, determine the:
(i)The area of the sheet needed for making the box.
(ii)The cost of the separate sheet for it, if a sheet measuring 1m² cost Rs. 20.
Solution: Given: The length (l) of the given box = 1.5m
The breadth (b) of the given box = 1.25 m
The depth (h) of the given box = 0.65m
(i) Box is to be open at the top
The area of the sheet needed.
= 2 x length x height + 2 x breadth x height + 2 x length x breadth.
= [ 2 × 1.5 × 0.65 + 2 × 1.25 × 0.65 + 1.5 × 1.25 ]m²
= (1.95 + 1.625 + 1.875) m²
= 5.45 m²
(ii) The cost of a sheet per m² Area = Rs.20.
The cost of a sheet of 5.45 m² area = Rs (5.45×20)
= Rs.109.
|
40 videos|470 docs|56 tests
|
FAQs on Class 9 Maths Chapter 11 Question Answers - Surface Areas and Volumes
| 1. What is the formula for the surface area of a sphere? |  |
| 2. How do you calculate the volume of a cylinder? |  |
| 3. What is the difference between surface area and volume? |  |
| 4. How do you find the total surface area of a cone? |  |
| 5. Can you explain how to derive the volume of a rectangular prism? |  |






















