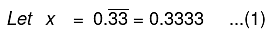Class 9 Exam > Class 9 Notes > Mathematics (Maths) Class 9 > Short Question Answers: Number System
Class 9 Maths Chapter 1 Question Answers - Number System
Q1. Find a rational number between 1 and 2.
Let x = 1 and y = 2, then
Thus, 3/2 is a rational number between 1 and 2.
Q2. Find two rational numbers between 0.1 and 0.3.
Let x = 0.1, y = 0.3 and n = 2
∴ Two rational numbers between 0.1 and 0.3 are: x + d and x + 2d
Q3. Express 
in the form of a decimal.
We have,
Now, dividing 25 by 8,
Since, the remainder is 0.
∴ The process of division terminates.
Q4. Express 
as a rational number.
Multiplying (1) by 100, we have 100x = 100 x 0.3333…
⇒ 100x = 33.3333 …(2)
Subtracting (2) from (1), we have
100x – x = 33.3333… – 0.3333…
⇒ 99x = 33
Q5. Simplify: (4+ √3) (4 −√3)
∵ (a + b)(a – b) = a2 – b2
(4 +√3) (4 −√3) = (4)2 – ( √3)2 = 16 – 3 = 13
Thus, (4 +√3) (4 −√3) = 13
Q6. Simplify: (√3 +√2)2
∵ (a + b)2 = a2 + 2ab + b2
(√3 +√2)2 = (√3)2 + √2 ( √3 ×2) + (√2)2 = 3 + 2 √6 + 2 = 5 + 2 √6
Thus, (√3 +√2)2 = 5 + 2√6
Q7. Rationalise the denominator of 
Since RF of (√x - √y ) is (√x +√y )
∴ RF of (√3 - √2 ) is (√3 +√2 )
Now, we have
Thus,
Q8. Find 
As, 64 = 4 x 4 x 4 = 43
Q9. Find a rational number lying between 
Rational numbers between 1/2 and 1/5 are infinite. Some of them are 3/10 , 4/10 , 45/100 , 35/100. Step-by-step explanation: As per the question, We need to find drational numbers lying between 1/5 and 1/2 As we know,Hence, Rational numbers between 1/2 and 1/5 are infinite. Some of them are 3/10 , 4/10 , 45/100 , 35/100.
- Rational Numbers are numbers that can be expressed in the form of p/q where q is not equal to zero.
- Now, we know that 1/5 = 0.2 and 1/2 = 0.5
- So, numbers between 0.2 and 0.5 are infinite. Some of them are 0.3,0.4,0.45,,0.35 etc.
- And these may be written as 3/10,4/10,45/100,35/100 tec.
Q10. Express 
as a fraction in the simplest form.
Let X =
Then, multiplying (1) by 10,
We have 10X = 10 x 0.24545...
⇒ 10x = 2.4545 ... (2)
Again multiplying (1) by 1000,
we get 1000 x X = 0.24545... x 1000
⇒ 1000X = 245.4545 ... (3)
Subtracting (2) from (3),
1000X – 10X = 245.4545... – 2.4545...
Thus
The document Class 9 Maths Chapter 1 Question Answers - Number System is a part of the Class 9 Course Mathematics (Maths) Class 9.
All you need of Class 9 at this link: Class 9
|
44 videos|412 docs|55 tests
|
FAQs on Class 9 Maths Chapter 1 Question Answers - Number System
| 1. What is the decimal number system? |  |
Ans. The decimal number system is a base-10 number system that uses the digits 0-9 to represent numbers. Each digit's position in a number determines its value, with the rightmost digit representing ones, the next representing tens, and so on.
| 2. How does the binary number system work? | |
Ans. The binary number system is a base-2 number system that uses only the digits 0 and 1 to represent numbers. Each digit's position in a binary number represents a power of 2, with the rightmost digit representing 2^0, the next representing 2^1, and so on.
| 3. What is the hexadecimal number system? | |
Ans. The hexadecimal number system is a base-16 number system that uses the digits 0-9 and the letters A-F to represent numbers. Each digit in a hexadecimal number represents a power of 16, with the rightmost digit representing 16^0, the next representing 16^1, and so on.
| 4. How can numbers be converted between different number systems? | |
Ans. Numbers can be converted between different number systems by using the concept of place value. To convert a number from one system to another, you can convert it to its decimal equivalent first and then convert it to the desired number system.
| 5. Why are different number systems used in computing? | |
Ans. Different number systems, such as binary and hexadecimal, are used in computing because they align well with the way computers process data. Binary is the fundamental number system in computing because computers use switches that can be in two states (on/off), making it easy to represent data using 0s and 1s. Hexadecimal is used as a shorthand for binary in programming and allows for more compact representation of data.
About this Document
|
18.3K Views |
|
4.74/5 Rating |
|
Nov 24, 2024 Last updated |
Document Description: Short Question Answers: Number System for Class 9 2024 is part of Mathematics (Maths) Class 9 preparation.
The notes and questions for Short Question Answers: Number System have been prepared according to the Class 9 exam syllabus. Information about Short Question Answers: Number System covers topics
like and Short Question Answers: Number System Example, for Class 9 2024 Exam. Find important definitions, questions, notes, meanings, examples, exercises and tests below for Short Question Answers: Number System.
Introduction of Short Question Answers: Number System in English is available as part of our Mathematics (Maths) Class 9
for Class 9 & Short Question Answers: Number System in Hindi for Mathematics (Maths) Class 9 course.
Download more important topics related with notes, lectures and mock test series for Class 9
Exam by signing up for free. Class 9: Class 9 Maths Chapter 1 Question Answers - Number System
Description
Full syllabus notes, lecture & questions for Class 9 Maths Chapter 1 Question Answers - Number System - Class 9 | Plus excerises question with solution to help you revise complete syllabus for Mathematics (Maths) Class 9 | Best notes, free PDF download
Information about Short Question Answers: Number System
In this doc you can find the meaning of Short Question Answers: Number System defined & explained in the simplest way possible. Besides explaining types of
Short Question Answers: Number System theory, EduRev gives you an ample number of questions to practice Short Question Answers: Number System tests, examples and also practice Class 9
tests
|
Explore Courses for Class 9 exam
|
|
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.
Related Searches
Free
,shortcuts and tricks
,Objective type Questions
,ppt
,Class 9 Maths Chapter 1 Question Answers - Number System
,Class 9 Maths Chapter 1 Question Answers - Number System
,mock tests for examination
,Semester Notes
,Sample Paper
,Class 9 Maths Chapter 1 Question Answers - Number System
,Extra Questions
,Viva Questions
,video lectures
,practice quizzes
,past year papers
,MCQs
,study material
,Important questions
,Previous Year Questions with Solutions
,Summary
,Exam
;
Additional Information about Short Question Answers: Number System for Class 9 Preparation
Short Question Answers: Number System Free PDF Download
The Short Question Answers: Number System is an invaluable resource that delves deep into the core of the Class 9 exam.
These study notes are curated by experts and cover all the essential topics and concepts, making your preparation more efficient and effective.
With the help of these notes, you can grasp complex subjects quickly, revise important points easily,
and reinforce your understanding of key concepts. The study notes are presented in a concise and easy-to-understand manner,
allowing you to optimize your learning process. Whether you're looking for best-recommended books, sample papers, study material,
or toppers' notes, this PDF has got you covered. Download the Short Question Answers: Number System now and kickstart your journey towards success in the Class 9 exam.
Importance of Short Question Answers: Number System
The importance of Short Question Answers: Number System cannot be overstated, especially for Class 9 aspirants.
This document holds the key to success in the Class 9 exam.
It offers a detailed understanding of the concept, providing invaluable insights into the topic.
By knowing the concepts well in advance, students can plan their preparation effectively.
Utilize this indispensable guide for a well-rounded preparation and achieve your desired results.
Short Question Answers: Number System Notes
Short Question Answers: Number System Notes offer in-depth insights into the specific topic to help you master it with ease.
This comprehensive document covers all aspects related to Short Question Answers: Number System.
It includes detailed information about the exam syllabus, recommended books, and study materials for a well-rounded preparation.
Practice papers and question papers enable you to assess your progress effectively.
Additionally, the paper analysis provides valuable tips for tackling the exam strategically.
Access to Toppers' notes gives you an edge in understanding complex concepts.
Whether you're a beginner or aiming for advanced proficiency, Short Question Answers: Number System Notes on EduRev are your ultimate resource for success.
Short Question Answers: Number System Class 9 Questions
The "Short Question Answers: Number System Class 9 Questions" guide is a valuable resource for all aspiring students preparing for the
Class 9 exam. It focuses on providing a wide range of practice questions to help students gauge
their understanding of the exam topics. These questions cover the entire syllabus, ensuring comprehensive preparation.
The guide includes previous years' question papers for students to familiarize themselves with the exam's format and difficulty level.
Additionally, it offers subject-specific question banks, allowing students to focus on weak areas and improve their performance.
Study Short Question Answers: Number System on the App
Students of Class 9 can study Short Question Answers: Number System alongwith tests & analysis from the EduRev app,
which will help them while preparing for their exam. Apart from the Short Question Answers: Number System,
students can also utilize the EduRev App for other study materials such as previous year question papers, syllabus, important questions, etc.
The EduRev App will make your learning easier as you can access it from anywhere you want.
The content of Short Question Answers: Number System is prepared as per the latest Class 9 syllabus.
|
© EduRev
|
Education Revolution
|
Follow Us
|
Signup to see your scores
go up within 7 days!
Access 1000+ FREE Docs, Videos and Tests
Takes less than 10 seconds to signup