Short & Long Answer Questions: Work, Energy & Power | Physics for ACT PDF Download
Short Answer Type Questions
Q.1 (a). If a force acts perpendicular to the Action of motion of a body, what is the amount of done? (b). A body is moving at constant speed over a frictionless surface. What is the work done by the weight?
Answer: (a). The work done is zero because there is no Placement in the direction of force.
(b). Work done by the weight is zero, since the force and the displacement are at right angles to each other.
 Q.2 The earth moving around the sun in a circular orbit is acted upon by a force and hence work must be done on the earth by the force. Do you agree by this statement?
Q.2 The earth moving around the sun in a circular orbit is acted upon by a force and hence work must be done on the earth by the force. Do you agree by this statement?
Answer: The statement is wrong. The gravitational force is a conservative force. So the work done by the gravitational force over every complete orbit of the earth is zero.
Q.3 A body is moving along a circular path. How much work is done by the centripetal force?
Or
Why is the work done by centripetal force zero?
Answer: For a body moving along a circular path, the centripetal force acts along the radius while the displacement is tangential i.e., θ=90∘,, therefore W =Fscos 90∘=0.
Q.4 A body of mass m is moving in a circle of radius r with a constant speed v. The force on the body is mυ2/r and is directed towards the center. What is the work done by this force in moving the body over half the circumference of the circle?
Answer: Work done by the force is zero, because the direction of displacement of the body at every point is perpendicular to the direction of force acting on the body.
Q.5 Is it possible that a body be in accelerated motion under a force acting on the body, yet no work is being done by the force? Explain your answer giving a suitable example.
Answer: Yes, it is possible, when the force is perpendicular to the direction of motion. The moon revolves round the earth under the centripetal force of attraction of the earth, but earth does no work on the moon.
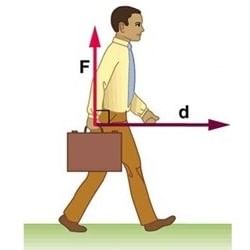
Q.6 How much work is done by a coolie walking on a horizontal platform with a load on his head?
Answer: Zero. In order to balance the load on his head, the coolie applies a force on it in the upward direction equal to its weight. His displacement is along the horizontal direction. Thus the angle between force 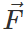 and displacement
and displacement 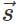 is 90∘. Therefore work done, W=Fs cosθ =Fs cos90∘=0.
is 90∘. Therefore work done, W=Fs cosθ =Fs cos90∘=0.
Q.7 A porter moving vertically up the stairs with a suitcase on his head does work. Why?
Answer: The porter lifts the suitcase vertically to the upstairs. Force has to be applied on the suitcase against the force of gravitation. Hence the porter does work.
Q.8 Does the work done in raising a suitcase on to a platform depend upon how fast it is raised up?
Answer: No. The work done depends on the force of gravity and the height through which the suitcase is raised. It does not depend on the time rate with which the suitcase is raised.
Q.9 In a tug of war one team is slowly giving way to the other. What work is being done and by whom?
Answer: The work is done by the winning team and is equal to the product of resultant force applied by the two teams and displacement that the losing team suffers.
Q.10 A man rowing boat upstream is at rest with respect to the shore. Is he doing work?
Answer: The boat is at rest with respect to the shore but it is moving upstream with respect to water. The man is doing work relative to the stream because he is applying force to produce relative motion between the boat and the stream. But he does no work relative to the shore as displacement relative to the shore is zero.
Q.11 Mountain roads rarely go straight up but wind up gradually. Why?
Answer: If the roads go straight up, the angle of slope θ would be large. In that case frictional force (f= μ mgcosθ) would be less and the vehicles may slip. Moreover, while going up a large slope, a greater power would be required (as it will take less time).
Q.12 What sort of energy is associated with a bird flying in air?
Answer: A flying bird possesses both potential and kinetic energies because it is at a certain height above the ground and moving with certain velocity.
Q.13 When an arrow is shot, where from the arrow will acquire its kinetic energy?
Answer: A stretched bow possesses potential energy on account of a change in its shape. To shoot an arrow, the bow is released. The potential energy of the bow is converted into the kinetic energy of the arrow.
Q.14 Can a body have energy without momentum?
Answer: Yes, there is an internal energy in a body due to the thermal agitation of the particles of the body, while the vector sum of the momenta of the moving particles may be zero.
Q.15 Can a body have momentum without energy?
Answer: No, if a body has momentum, it must be in motion and consequently possess kinetic energy.
Q.16 A light body and a heavy body have the same momentum. Which one will have greater kinetic energy? Or Two bodies of unequal masses have same linear momentum, which one has greater kinetic energy?
Answer: Kinetic energy, 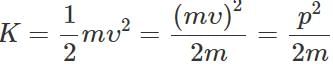 For constant p, K∝ 1/m Thus the lighter body has more kinetic energy than the heavier body.
For constant p, K∝ 1/m Thus the lighter body has more kinetic energy than the heavier body.
Q.17 A light body and a heavy body have the same kinetic energy. Which one will have the greater momentum?
Answer: Kinetic energy, 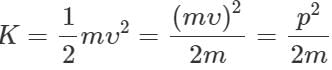 or
or 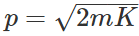 i.e., p∝√m Thus the heavier body has a greater momentum than the lighter one.
i.e., p∝√m Thus the heavier body has a greater momentum than the lighter one.
Q.18 How does the kinetic energy of a body change if its momentum is doubled?
Answer:
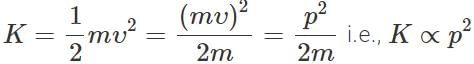 When the momentum of a body is doubled, its kinetic energy becomes four times the initial kinetic energy.
When the momentum of a body is doubled, its kinetic energy becomes four times the initial kinetic energy.
Q.19 Two bodies of masses m1 and m2 have the same linear momentum. What is the ratio of their kinetic energies?
Answer: If υ1 and υ2 are the velocities of two bodies having masses m1 and 2 respectively, then m1υ1=m2υ2 or m21υ21=m22υ22 or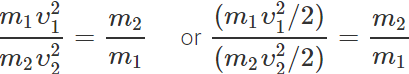 or
or 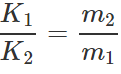
Q.20 Two bodies of masses m1 and m2 have equal kinetic energies. What is the ratio of their linear momenta?
Answer: 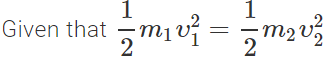 or
or 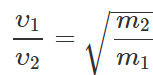 or
or 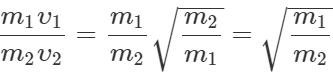 or
or 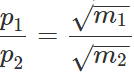
Q.21 Can there be a situation in which E−U<0?
Answer: No. As E=K+U or K=E−U But kinetic energy K cannot be negative. So E−U is never less than zero.
Q.22 Can the overall energy of a body be negative?
Answer: Yes. As E=K+U,when U is negative and has magnitude greater than that of K, E is negative. For example, the energy of an electron bound to the nucleus of an atom is negative.
Q.23 Does the potential energy of a spring decrease or increase when it is compressed or stretched?
Answer: The potential of the spring increases because work is done on it when it is compressed or stretched.
Q.24 If a block attached to a spring (whose other end is rigidly fixed) is pulled up to distance x0 and released, the amplitude of its motion cannot exceed ±x0. Why?
Answer: If the amplitude of motion exceeds ±x0,, then the potential energy would be greater than 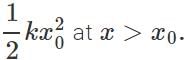 So its K.E. =
So its K.E. = 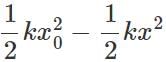 would be negative. This is impossible. Hence the block cannot go beyond x=±x0.
would be negative. This is impossible. Hence the block cannot go beyond x=±x0.
Q.25 Springs A and B are identical except that A is stiffer than B, i.e., force constant kA>kB. In which spring is more work expended if they are stretched by the same amount?
Answer: Work done in stretching a spring of force constant k through a distance x,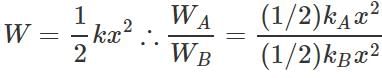

Q.26 Springs A and B are identical except that A is stiffer than B. In which spring is more work expended if they are stretched by the same force?
Answer: 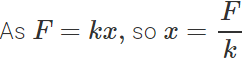 For same
For same 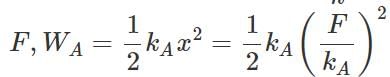
and 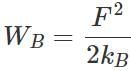 ∴
∴ 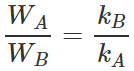 As kA>kB therefore, WA<WB.
As kA>kB therefore, WA<WB.
Q.27 Which of the two: kilowatt hour or electron volt is a bigger unit of energy and by what factor?
Answer: Kilowatt hour (kWh) is a bigger unit of energy.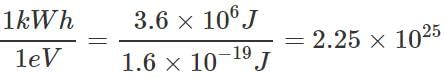
Q.28 Will water at the foot of the fall be at a different temperature from that at the top? If yes, explain.
Answer: When water falls from a height, its P.E. is converted into kinetic energy and its velocity is maximum at the foot of the fall. The velocity is suddenly reduced to zero, and hence its kinetic energy gets converted into heat energy raising its temperature.
Q.29 Is it necessary that work done in the motion of a body over a closed loop is zero for every force in nature? Why?
Answer: No. The work done in the motion of body over a closed loop is zero only in case of a conservative force but it is not zero in case of a non-conservative force like friction.
Q.30 When a constant force is applied to a body moving with constant acceleration, is the power of the force constant? If not, how would force have to vary with speed for power to be constant?
Answer: Power, P=Fυ As the body is moving with acceleration, υ changes and so P also changes, F being constant. For P to be constant, Fυ=a constant or(F∝1/υ). Thus as υ increases, F should decrease to keep P constant.
Q.31 What are central forces? Are they conservative in nature?
Answer: Force between two objects is called a central force, if it acts between them along the line joining their centers. Electrostatic force between the charges and magnetic force between two poles are central forces and are conservative forces.
Q.32 When is the exchange of energy maximum during an elastic collision?
Answer: Energy exchange will be maximum if the two colliding bodies are of equal masses.
Q.33 Is whole of the kinetic energy lost in any perfectly inelastic collision?
Answer: No, only that much amount of kinetic energy is lost as is necessary for the conservation of momentum.
Q.34 Can you associate potential energy with a non-conservative force?
Answer: No, P.E. can be associated only with conservative force.
Q.35 Two bodies moving towards each other collide and move away in opposite directions. There is some rise of temperature of the bodies in the process. Explain the reason for the rise of temperature and state what type of collision is it.
Answer: Involved collision of the process is inelastic because the bodies suffer loss of kinetic energy which appears in the form of heat energy raising the temperature of the bodies.
Q.36 A spark is produced, when two stones are struck against each other. Why?
Answer: The work done in striking the two stones against each other gets converted into heat. This appears as a spark.
Q.37 A lorry and a car with the same kinetic energy are brought to rest by the application of the brakes which provide equal retarding force. Which of them will come to rest in a shorter distance?
Answer: By work-energy theorem, Loss in K.E. of the vehicle =Work done against retarding force =Retarding force x distance travelled ∴Distance travelled 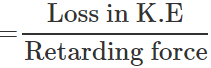 As both the kinetic energy and retarding force are same, so both the lorry and the car would come to rest in the same distance.
As both the kinetic energy and retarding force are same, so both the lorry and the car would come to rest in the same distance.
Q.38 A truck and a car are moving with the same kinetic energy on a straight road. Their engines are simultaneously switched off. Which one will stop at a lesser distance?
Answer: By work-energy theorem, Loss in K.E. of the vehicle =Work done against the force of friction x distance or K.E. =f×s=μR×s=μmg s or 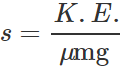 For constant K.E., s∝ 1/m As the truck has more mass than the car, so it will stop in a lesser distance than the car.
For constant K.E., s∝ 1/m As the truck has more mass than the car, so it will stop in a lesser distance than the car.
Q.39 A rocket explodes in mid air. How does this affect (a) its total momentum and (b) its total kinetic energy?
Answer: (a) Because no external force acts on the rocket, its total momentum remains unchanged. (b) When the rocket explodes, its fragments receive additional kinetic energy from the explosion. The chemical energy of the fuel changes into kinetic energy. As a result of this, the total kinetic energy gets increased.
Q.40 The velocity of an aeroplane is doubled. (a) What will happen to its momentum? Will the momentum remain conserved? (b) What will happen to its K.E.? Will the energy remain conserved?
Answer: (a) when the velocity of the aeroplane is doubled, its momentum also gets doubled. However, the combined momentum of aeroplane + air is conserved. As the momentum of the aeroplane increases, the momentum of air also increases by an equal amount in the opposite direction. (b) The kinetic energy becomes four times. The additional energy is obtained by burning of fuel. However, the total energy is still conserved.
Long Answer Type Questions
Q.41 A pump on the ground floor of a building can pump up water to fill a tank of volume 30m3 in 15 min. If the tank is 40 m above the ground, and the efficiency of the pump is 30%, how much electric power is consumed by the pump?
Answer: In the above question it is given that:
Volume of the tank, V = 30m3.
Time of operation, t = 15 min = 15 × 60 = 900 s .
Height of the tank, h = 40 m .
Efficiency of the pump, η = 30
Density of water, ρ = 103kg/m3
Mass of water, m = ρV = 30 × 103kg
Output power can be obtained as: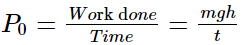
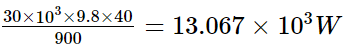
For input power, efficiency is given by the relation: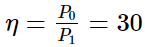
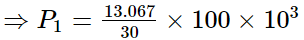
⇒ P1 = 43.6kW, which is the required power consumption.
Q.42 Prove that in an elastic collision in one dimension the relative velocity of approach before impact is equal to the relative velocity of separation after impact.
Answer: Consider the figure given below: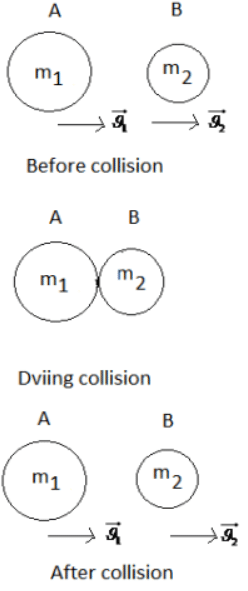 According to law of conservation of linear momentum
According to law of conservation of linear momentum
m1u1 + m2u2 = m1v1 + m2v2
m1(u1 − v1) = m2(v2 − u2) …… (1)
K.E. also remains conserved.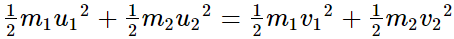
m1(u12 − v12) = m2(v22 − u22) …… (2)
Dividing (2) by (1)
u1 − v1 = v2 + u2
u1 − u2 = v2 − v1
i.e., Relative velocity of approach = Relative velocity of separation .
Q.43 Develop a relation between the co-efficient of linear expansion, co-efficient superficial expansion and coefficient of cubical expansion of a solid.
Answer: As the co−efficient of linear expansion = α = ΔL/LΔT
Where, ΔL = change in length
L = length
ΔT = change in temperature .
In the same way,
Co−efficient of superficial expansion = β = ΔS/SΔT
ΔS = change in area
S = original area
ΔT = change in temperature
Co-efficient of cubical expansion, Y = ΔV/VΔT
ΔV = change in volume
V = original volume
ΔT = change in temperature .
Now,
ΔL = αL ΔT
⇒L + ΔL = L + αL ΔT
⇒L + ΔL = L (1 + αΔT) …… (1)
Similarly, V+ ΔV = V (1 + YΔT) ……. (2)
And
S + ΔS = S (1 + βΔT) …… (3)
Also,
(V + ΔV) = (L + ΔL)3
⇒ V + ΔV = L3(1 + 3αΔT + 3α2ΔT2 + α3T3)
Since α2, α3 are negligible,
so,
V + γ VΔT= V(1 + 3αΔT) [as L3 = V]
So,
V + γVΔT = V + V3αΔT
⇒ γVΔT = 3αΔT
⇒ γ = 3α
Similarly, β = 2α (using L2 = S (Area) )
So, α = β/2 = γ/3 , which is the required relation.
Q.44 A trolley of mass 200 kg moves with a uniform speed of 36 km/h on a frictionless track. A child of mass 20 kg runs on the trolley from one end to the other (10 m away) with a speed of 4 relative to the trolley in a direction opposite to its motion, and jumps out of the trolley. What is the final speed of the trolley? How much has the trolley moved from the time the child begins to run?
Answer: In the above question it is given that:
Mass of the trolley, M = 200 kg .
Speed of the trolley, v = 36 km/h = 10 m/s .
Mass of the boy, m = 20 kg .
Initial momentum of the system of the boy and the trolley
= (M + m)v = (200 + 20) × 10 = 2200 kg m/s
Let v' be the final velocity of the trolley with respect to the ground.
Final velocity of the boy with respect to the ground = v′ − 4
Final momentum = Mv′ + m(v′ − 4)
= 200v′ + 20v′ − 80 = 220v′ − 80
As per the law of conservation of momentum:
Initial momentum = Final momentum 2200 = 220v′ − 80
⇒ v′ = 2280/220 = 10.36m/s
Length of the trolley, l = 10 m .
Speed of the boy, v′′ = 4 m/s .
Time taken by the boy to run, t = 104 = 2.5s.
Thus, the distance moved by the trolley = v′′ × t = 10.36 × 2.5 = 25.9m.
Q.45 An electron and a proton are detected in a cosmic ray experiment, the first with kinetic energy 10 keV, and the second with 100 keV. Which is faster, the electron or the proton? Obtain the ratio of their speeds.
(electron mass = 9.11 × 10−31 kg , proton mass = 1.67 × 10−27 kg , 1 eV = 1.60 × 10−19J ).
Answer: In the above question it is given that:
Mass of the electron = 9.11 × 10−31 kg
Mass of the proton = 1.67 × 10−27 kg
Kinetic energy of the electron, EKe = 10 keV = 104eV
= 104 × 1.60 × 10−19 = 1.60 × 10−15J
Kinetic energy of the proton, EKp = 100keV = 105eV = 1.60 × 10−14J.
For the velocity of an electron ve, its kinetic energy is given by the relation: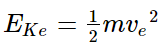
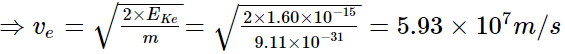
Hence, the electron is moving faster than the proton.
The ratio of their speeds: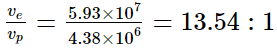
It is clear that electrons are faster; Ratio of speeds is 13.54 : 1 .
Q.46 (a) Define potential energy. Give examples.
(b) Draw a graph showing the variation of potential energy, kinetic energy and the total energy of a body freely falling on earth from a height h?
Answer: (a) Potential energy is defined as the energy possessed by a body by virtue of its position in a field or due to change in its configuration example – A gas compressed in a cylinder, A wound spring of a water, water raised to the overhead tank in a house etc.
(b) The graph below shows the variation of potential energy, kinetic energy and the total energy of a body freely falling on earth from a height h: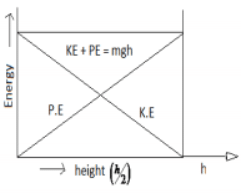 (i) Gravitational potential energy decreases as the body falls downwards and is zero at the earth
(i) Gravitational potential energy decreases as the body falls downwards and is zero at the earth
(ii) Kinetic energy increases as the body falls downwards and is maximum when the body just strikes the ground.
(iii) According to the law of conservation of energy, total mechanical (KE + PE) energy remains constant.
Q.47 Two identical ball bearings in contact with each other and resting on a frictionless table are hit head-on by another ball bearing of the same mass moving initially with a speed V. If the collision is elastic, which of the following figures is a possible result after collision?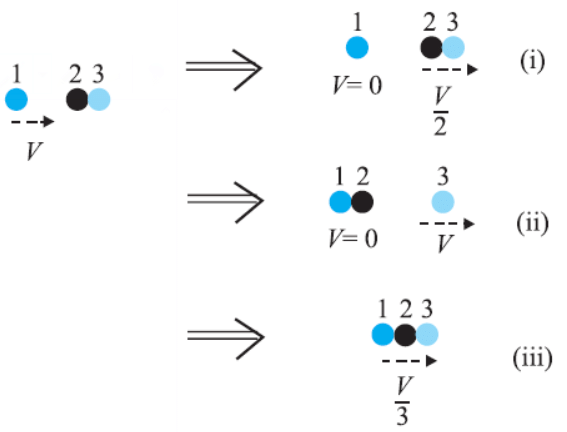 Answer: Case: (i) Result is possible after a collision
Answer: Case: (i) Result is possible after a collision
It is observed that the total momentum before and after collision in each case is constant. For an elastic collision, the total kinetic energy of a system remains conserved before and after the collision. For the mass of each ball bearing m,
The total kinetic energy of the system before collision: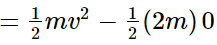
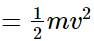
Case (ii): Total kinetic energy of the system after collision

Hence, the kinetic energy of the system is not conserved in case (i).
Case (iii): Total kinetic energy of the system after collision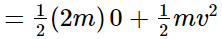
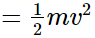
Q.48 A bullet of mass 0.012 kg and horizontal speed of 70m/s strikes a block of wood of mass 0.4 kg and instantly comes to rest with respect to the block. The block is suspended from the ceiling by means of thin wires. Calculate the height to which the block rises. Also, estimate the amount of heat produced in the block.
Answer: In the above question it is given that:
Mass of the bullet, m = 0.012 kg
Initial speed of the bullet, ub = 70 m/s.
Mass of the wooden block, M = 0.4 kg
Initial speed of the wooden block, ug = 0
Final speed of the system of the bullet and the block = v
Applying the law of conservation of momentum:
mub + Mug = (m + M)v
0.012 × 70 + 0.4 × 0 = (0.012 + 0.4)v
⇒ v = 0.84/0.412 = 2.041m/s
For the system of the bullet and the wooden block:
Mass of the system, m′ = 0.412 kg
Velocity of the system = 2.04 m/s
Height up to which the system rises = h
Applying the law of conservation of energy to this system:
Potential energy at the highest point = Kinetic energy at the lowest point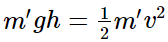

The wooden block will rise to a height of 0.2123 m.
Heat produced = Kinetic energy of the bullet − Kinetic energy of the system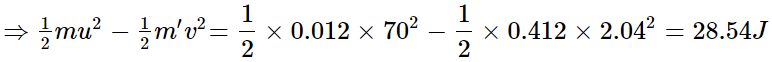
Q.49 A rain drop of radius 2 mm falls from a height of 500 m above the ground. It falls with decreasing acceleration (due to viscous resistance of the air) until at half its original height, it attains its maximum (terminal) speed, and moves with uniform speed thereafter. What is the work done by the gravitational force on the drop in the first and second half of its journey? What is the work done by the resistive force in the entire journey if its speed on reaching the ground is 10m/s?
Answer: In the above question it is given that:
Radius of the rain drop, r = 2 mm = 2×10−3m .
Volume of the rain drop, 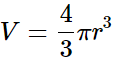
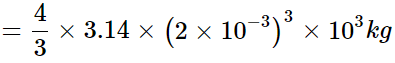
Density of water, ρ = 103kg/m3
Mass of the rain drop, m = ρV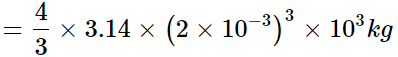
Gravitational force, F = mg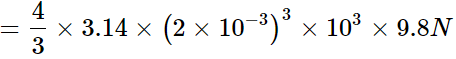
The work done by the gravitational force on the drop in the first half of its journey:
W1 = Fs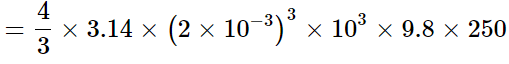
= 0.082 J
This amount of work is equal to the work done by the gravitational force on the drop in the second half of its journey, i.e., WII = 0.082 J As per the law of conservation of energy, if no resistive force is present, then the total energy of the rain drop will remain the same.
Total energy at the top will be:
ET = mgh + 0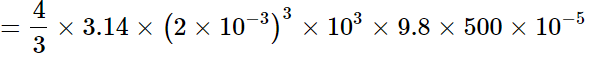
=0.164 J
Due to the presence of a resistive force, the drop hits the ground with a velocity of 10 m/s.
Total energy at the ground will be: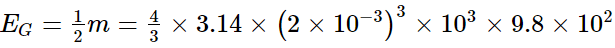
= 1.675 × 10−3J
Clearly, Work done by resistive force = EG − ET = −0.162J
Q.50 The blades of a windmill sweep out a circle of area A.
(a) If the wind flows at a velocity v perpendicular to the circle, what is the mass of the air passing through it in time t?
(b) What is the kinetic energy of the air?
(c) Assume that the windmill converts 25% of the wind's energy into electrical energy, and that A = 30m2 , v = 36 km/h and the density of air is 1.2 kg/m3 . What is the electrical power produced?
Answer: In the above question it is given that:
Area of the circle swept by the windmill = A
Velocity of the wind = v
Density of air = ρ
(a) Volume of the wind flowing through the windmill per sec = Av
Mass of the wind flowing through the windmill per sec = ρAv.
Mass m, of the wind flowing through the windmill in time t = ρAvt
(b) Kinetic energy of air 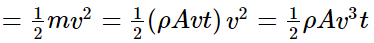
(c) Area of the circle swept by the windmill = A = 30 m2
Velocity of the wind = v = 36 km/h
Density of air, ρ = 1.2kg/m3
Electric energy produced = 25

Also,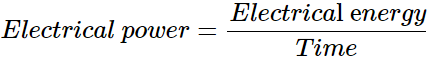
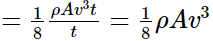
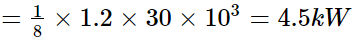
|
169 videos|131 docs|69 tests
|
















