Class 9 Maths Chapter 5 Question Answers - Introduction to Euclid`s Geometry
Q1: What are the five postulates of Euclid’s Geometry?
Sol: Euclid’s postulates were:
- A straight line may be drawn from one point to any other point.
- A terminated line can be produced indefinitely.
- A circle can be drawn with any centre and any radius.
- All right angles are equal to one another.
- If a straight line falling on two straight lines makes the interior angles on the same side of it taken together less than two right angles, then the two straight lines if produced indefinitely, meet on that side on which the sum of angles is less than two right angles.
Q2: If in Q.2, point C is called a mid-point of line segment AB. Prove that every line segment has one and only one mid-point.
Sol: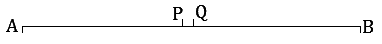 Let, AB be the line segment
Let, AB be the line segment
Assume that points P and Q are the two different midpoints of AB.
Therefore,
AP=PB ………(1)
and AQ = QB …..(2)
Also,
PB + AP = AB (as it coincides with line segment AB)
Similarly, QB + AQ = AB.
Now,
Adding AP to the L.H.S and R.H.S of the equation (1)
We get, AP + AP = PB + AP (If equals are added to equals, the wholes are equal.)
⇒ 2 AP = AB — (3)
Similarly,
2 AQ = AB — (4)
From (3) and (4),
2 AP = 2 AQ
⇒ AP = AQ
Thus, we conclude that P and Q are the same points.
This contradicts our assumption that P and Q are two different midpoints of AB.
Thus, it is proved that every line segment has one and only one mid-point.
Hence Proved.
Q3: Does Euclid’s fifth postulate imply the existence of parallel lines? Explain.
Sol:
Yes, Euclid’s fifth postulate does imply the existence of the parallel lines.
If the sum of the interior angles is equal to the sum of the right angles, then the two lines will not meet each other at any given point, hence making them parallel to each other.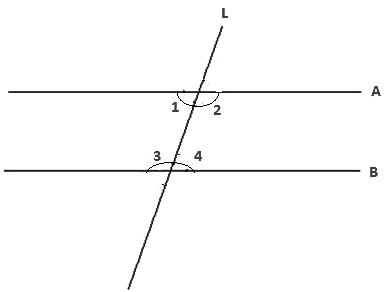 So,
So,
∠1+∠2=180°
Or ∠3+∠4=180°
Q4: If a point C lies between two points A and B such that AC = BC, then prove that AC =1/2 AB. Explain by drawing the figure.
Sol: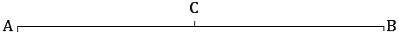 Given, AC = BC
Given, AC = BC
Now, add AC on both sides.
L.H.S + AC = R.H.S + AC
AC + AC = BC + AC
2AC = BC + AC
Since, we know,
BC +AC = AB (as it coincides with line segment AB, from figure)
∴ 2 AC = AB (If equals are added to equals, the wholes are equal.)
⇒ AC = 1/2 AB.
Q5: In the given figure, if AC = BD, then prove that AB = CD.
Sol: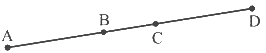 It is given, AC = BD
It is given, AC = BD
From the given figure, we get,
AC = AB + BC
BD = BC + CD
⇒ AB + BC = BC + CD [Given: AC=BD]
We know that, according to Euclid’s axiom, when equals are subtracted from equals, remainders are also equal.
Subtracting BC from the L.H.S and R.H.S of the equation AB + BC = BC + CD, we get,
AB + BC – BC = BC + CD – BC
AB = CD
Hence proved.
Q.6: It is known that x + y = 10 and that x = z. Show that z + y = 10.
Sol:
According to the question,
We have,
x+y=10 …(i)
And, x=z …(ii)
Applying Euclid’s axiom,
“if equals are added to equals, the wholes are equal”
We get,
From Eq. (i) and (ii)
x+y=z+y ….(iii)
From Eqs. (i) and (iii)
z+y = 10
|
40 videos|470 docs|56 tests
|





















