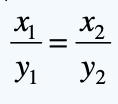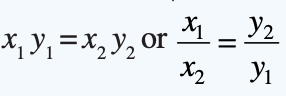Points to Remember- Direct and Inverse Proportions | Mathematics (Maths) Class 8 PDF Download
| Table of contents |

|
| Points to Remember |

|
| We Know That |

|
| Direct Proportion |

|
| Inverse Proportion |

|
| Solved Examples |

|
Points to Remember
- When two quantities, x and y, change in a way that their ratio stays the same, they are said to be in direct proportion.
- If x and y change such that when one increases, the other decreases proportionally (and the reverse is true), they are in inverse proportion.
- If x and y are in a direct proportion, then (x/y) = constant.
- If x and y are in an inverse variation, then (xy) = constant.
We Know That
- Variable Nature: The value of a variable is not constant and changes over time or circumstances.
- Inter-Related Quantities: Some quantities have a relationship with others, meaning when one changes, the other also changes. This interrelation is known as variation.
- Types of Variation:There are two types of variation: (i) Direct Variation (ii) Inverse Variation
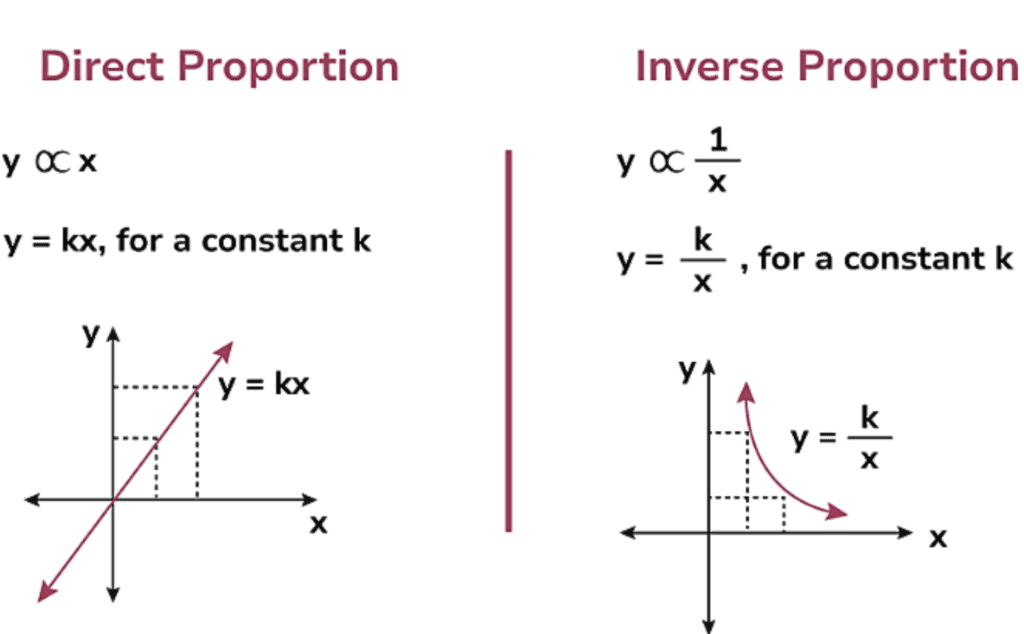
Direct Proportion
If two quantities are related in such a way that an increase in one quantity leads to increase in the other and vice versa, then this is a case of direct variation. Also, a decrease in one quantity brings a corresponding decrease in the other.
Two quantities x and y are said to be in direct proportion, if
(x/y) = k or x = ky
Note:
I. In a direct proportion two quantities x and y vary with each other such that (x/y) remains constant.
II. (x/y) is always a positive number.
III. (x/y) or k is called the constant of variation.
Inverse Proportion
If two quantities change in such a manner that, if one quantity increases, the other quantity decreases in the same proportion and vice versa, then it is called Inverse Proportion.
Two quantities x and y are said to be in inverse proportion,if x ∝ (1 / y)
x = k / y ⇒ xy = k
Note:
I. In an inverse proportion, two quantities x and y vary with each other such that xy remains constant.
II. x × y is always a positive number.
III. x × y or k is called the constant of variation in inverse proportion.
Solved Examples
Q 1: Following are the car parking charges near an Airport up to
a. 2 hours Rs 60
b. 6 hours Rs 100
c. 12 hours Rs 14
d. 24 hours Rs 180
Check if the parking charges are in direct proportion to the parking time.
Solution: We know that two quantities are in direct proportion if whenever the values of one quantity increase, then the value of another quantity increase in such a way that ratio of the quantities remains same. Here, the charges are not increasing in direct proportion to the parking time because of 2/60 ≠ 6/100 ≠ 12/140 ≠ 24/180
Q 2: y is directly proportional to x, and y = 24 when x = 4. What is the value of y when x = 3?
a. 18
b. 20
c. 23
d. 43
Ans : a
Solution: Step 1 Find the constant of proportionality:
y is directly proportional to x ⇒ y ∝ x ⇒ y = kx where k is the constant of proportionality.
But y = 24 when x = 4
⇒ 24 = k × 4
⇒ k = 6
Step 2 Write down the equation connecting y and x:
y = kx ⇒ y = 6x
Step 3 Substitute x = 3 into this equation to find the corresponding value of y:
When x = 3, y = 6 × 3 = 18
Q 3. The circumference (C cm) of a circle is directly proportional to its diameter (d cm). The circumference of a circle of diameter 3.5 cm is 11 cm. What is the circumference of a circle of diameter 4.2 cm?
a. 9.17 cm
b. 11.7 cm
c. 13.2 cm
d. 14 cm
Ans: c
Solution: We are told C = 11 when d = 3.5
We need to find the value of C when d = 4.2Step 1 Find the constant of proportionality:
C is directly proportional to d ⇒ C ∝ d ⇒ C = kd where k is the constant of proportionality.
But C = 11 when d = 3.5
⇒ 11 = k × 3.5
⇒ k = 11/3.5 = 22/7
|
81 videos|423 docs|31 tests
|
FAQs on Points to Remember- Direct and Inverse Proportions - Mathematics (Maths) Class 8
| 1. What is direct proportion and how is it different from inverse proportion? |  |
| 2. Can you provide a real-life example of direct proportion? |  |
| 3. How do you solve problems involving direct and inverse proportions? |  |
| 4. What are some key characteristics of direct and inverse proportions? |  |
| 5. How can understanding direct and inverse proportions help in everyday life? |  |