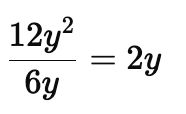Points to Remember- Factorisation | Mathematics (Maths) Class 8 PDF Download
What are Factors?
Factors are numbers, letters, or expressions that, when multiplied together, create a specific number or expression. Factorization simplifies complex expressions into easier parts for examination or use.
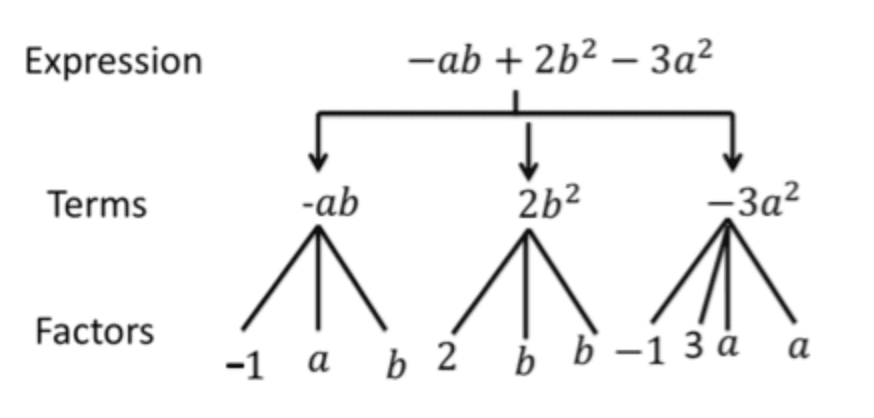
Factors of Algebraic expressions
- In algebraic expressions, terms are formed as products of factors.
For example, in 7xy + 4x, the term 7xy consists of factors 7, x, and y.
These factors are "irreducible" (cannot be further factored).
- The expression 6x (x + 3) demonstrates that 6, x, and (x + 3) are irreducible factors.
Similarly, 12 x (x + 3)(y + 5) is expressed in its irreducible factor form as 3⋅4⋅x⋅(x + 3)⋅(y + 5).
Note : 1 is a factor of every term but is usually not explicitly shown unless necessary.
Methods of Factorization
1. Factorization Using Common Factors
To factorize an algebraic expression, the highest common factors are determined.
Example 1:Factorise algebraic expression -2y2 + 8y
Solution: We have: -2y2 + 8y
On factorising the terms, we get :
−2y2= −1 × 2 × y × y
8y = 2 × 2 × 2 × y
The highest common factors of these terms are 2y
−2y2+8y = [ (− 1× 2 × y) × y ] + [ (2 × 2 × 2) × y]
=2 × y × (−y + 4)
Therefore, −2y2 + 8y = 2y(−y + 4)
Example 2: Factorise 18x2 – 14x3 + 10x4
Solution: We have
18x2= 2 × 3 × 3 × x × x
14x3=2 × 7 × x × x × x
10x4= 2 × 5 × x × x × x × xObviously, the common factors of these terms are 2, and two times x.
∴ 18x2 – 14x3 + 10x4
=[2 × 3 × 3 × x × x] − [2 × 7 × x × x × x] + [2 × 5 × x × x × x × x]
=[(2 × x × x) × 3 × 3]− [(2 × x × x ) × 7 × x] + [( 2 × x × x ) × 5 × x × x]
=(2 × x × x)[3 × 3 − 7 × x + 5 × x × x]
=2x2[ 9 − 7x + 5x2]
Thus, 18x2 – 14x3 + 10x4 = 2x2[9 – 7x + 5x2]
2. Factorisation By Regrouping Terms
In some algebraic expressions, it is not possible that every term has a common factor. Therefore, to factorise those algebraic expressions, terms having common factors are grouped together.
Example 1: Factorise 9x + 18y + 6xy + 27
Solution:Here, we have a common factor 3 in all the terms.
∴ 9x + 18y + 6xy + 27 = 3[3x + 6y + 2xy + 9]
We find that 3x + 6y = 3(x + 2y) and 2xy + 9 = 1(2xy + 9)
i.e. a common factor in both groups does not exist,
Thus, 3x + 6y + 2xy + 9 cannot be factorized.
On regrouping the terms, we have
3x + 6y + 2xy + 9 = 3x + 9 + 2xy + 6y
= 3(x + 3) + 2y(x + 3)
= (x + 3)(3 + 2y)
Now, 3[3x + 6y + 2xy + 9] = 3[(x + 3)(3 + 2y)]
Thus, 9x + 18y + 6xy + 27 = 3(x + 3)(2y + 3)
Example 2: Factorise 8xy−6y+4−12x
Solution: Step 1: Check if there is a common factor among all terms. There is none.
Step 2: Think of grouping. Notice that the first two terms have a common factor:
8xy − 6y= 2y (4x − 3)
For the last two terms:
4 − 12x = − 4(3x − 1)
Step 3: Putting the groups together:
8xy − 6y + 4 − 12x
= 2y(4x − 3) − 4(4x − 3)Factor out the common term (4x − 3):
=(4x − 3) (2y − 4)
The factors of 8xy − 6y + 4 − 12x are: (4x − 3) and (2y − 4)
3. Factorisation using identities
Some expressions can easily be factorized using these identities:
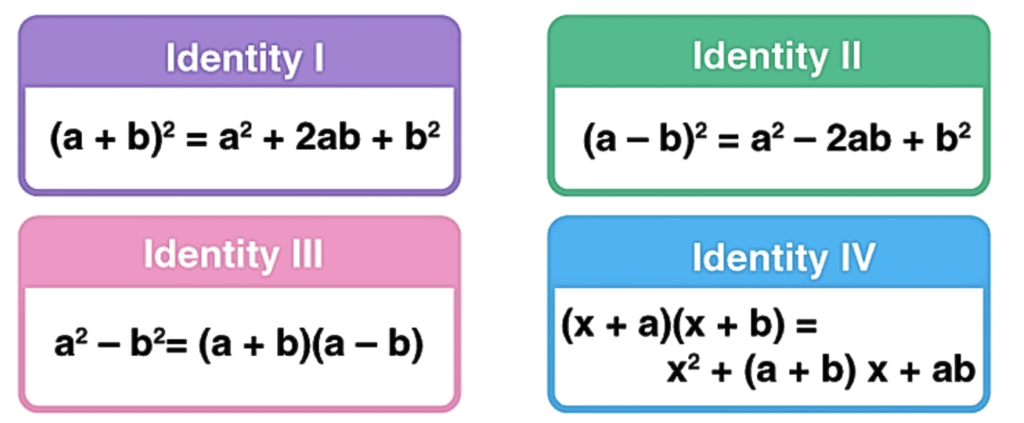
Example 1:Factorise 4x² – 20x + 25.
Solution: 4x² – 20x + 25
= (2x)² – 2 × 2x × 5 + (5)²
= (2x – 5)² --[Using the identity a² – 2ab + b² = (a – b)²]
Example 2: Factorise 64x2 − 25
Solution: There are two terms; both are squares and the second is negative. The expression is of the form (a2−b2).
= 64x2− 25 = (8x)2 − (5)2
Using identity a2 - b2 = (a + b) (a - b)
= (8x − 5) (8x + 5)
Example 2:Verify that : (11pq + 4q)² – (11pq – 4q)² = 176pq²
Solution: Solving L. H. S. = (11pq + 4q)² – (11pq – 4q)²
[ Using identities (a + b)² = (a² + 2ab + b²) and (a – b)² = (a² – 2ab + b²) ]
= 121p²q² + 88pq² + 16q² – (121p²q² – 88pq² + 16q²)
= 121p²q² + 88pq² + 16q² – 121p²q² + 88pq² – 16q²
= 88pq² + 88pq²
= 176pq²
L. H. S. = 176pq²
Therefore, L. H. S. = R. H. S. (verified)
Division of Algebraic Expressions
1. Division of a Monomial by Another Monomial:
- Write the irreducible factors of both the monomials.
- Cancel out the common factors between the numerator and denominator.
- The remaining terms form the answer.
Example: Divide 12y2 by 6y
Solution: Dividing 12y2 by 6y
2. Division of a Polynomial by a Monomial:
- Write the irreducible form of both the polynomial and monomial.
- Factorize the polynomial, if possible, to identify common terms.
- Cancel out the common factor between the terms.
- The remaining terms represent the final answer.
Example 1: Divide x6+7x5−5x4 by x2
Sol: Dividing x6+7x5−5x4 by x2
= x6+ 7x5− 5x4 ÷ x2Now, we need to divide each term of the polynomial by the monomial and simplify:
x⁶x² + 7x⁵x² - 5x⁴x²
= x⁴ + 7x³ - 5x²
3. Division of A Polynomial by another Polynomial:
- In the case of polynomials, reduce the terms and factorize using identities or by finding common terms.
- Cancel out common factors to find the result.
Example1: Solve (3x3 − 27x) ÷ 3x( x − 3)
Sol:
Factorize the polynomial:
3x3 - 27x = 3x(x2 - 9)
Using the identity (a2 - b2 = (a + b)(a - b):
3x(x2 - 9) = 3x(x + 3)(x - 3)
Divide by:
3x(x + 3)(x - 3)3x(x - 3)
Cancel the common factors 3x and (x - 3):
= x + 3
Some Solved Examples for You:
Q1: Factors of x2+ xy + 8x + 8y are :
A) (x + y)(x + 8)
B) (2x + y)(x + 8)
C) (x + 2y)(x + 8)
D) (x + 8)(x + y)
Solution: correct option is (A)
x2 + xy + 8x + 8y
Factorizing each term
= (x × x) + (x × y) + (8 × x)+ (8 × y)
On taking common from terms
=x(x + y) + 8(x+y)
=(x + y)(x + 8)
Q 2: Simplify 5(2x+1)(3x+5)÷(2x+1)
A) 10x + 5
B) 5(3x + 5)
C) 5(2x + 1)(3x + 5)
D) 3x + 5
Solution: correct option is (B)5(2x + 1)(3x + 5 ) ÷ (2x + 1) = 5(2x + 1)(3x + 5)(2x + 1)
= 5(3x + 5)
|
81 videos|423 docs|31 tests
|
FAQs on Points to Remember- Factorisation - Mathematics (Maths) Class 8
| 1. What are factors in algebraic expressions? |  |
| 2. How do you factor an algebraic expression using common factors? |  |
| 3. What is factorization by regrouping terms? |  |
| 4. How can identities be used in factorization? |  |
| 5. What is the process for dividing algebraic expressions? |  |