Integers Class 7 Notes Maths Chapter 1
Integers
A whole number, from zero to positive or negative infinity is called Integers. I.e. it is a set of numbers which include zero, positive natural numbers and negative natural numbers. It is denoted by letter Z.
Z = {…,-2,-1, 0, 1, 2…}
Integers on Number Line
On the number line, for positive integers we move to the right from zero and for negative integers move to the left of zero.
Facts about how to Add and Subtract Integers on the Number Line
1. If we add a positive integer, we go to the right.
2. If we add a negative integer, we go to the left.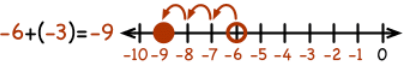
3. If we subtract a positive integer, we go to the left.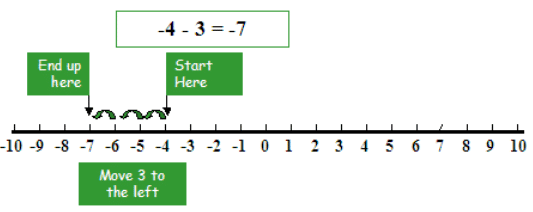
4. If we subtract a negative integer, we go to the right.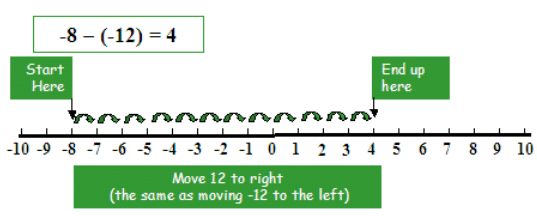
The Additive Inverse of an Integer
The negative of any number is the additive inverse of that number. The additive inverse of 5 is (- 5) and additive inverse of (- 5) is 5.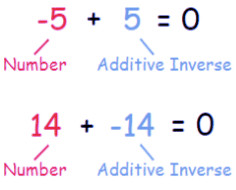
This shows that the number which we add to a number to get zero is the additive inverse of that number.
Number | Additive Inverse |
5 | - 5 |
14 | - 14 |
- 10 | 10 |
- 6 | 6 |
Properties of Addition and Subtraction of Integers
1. Closure under Addition
For the closure property the sum of two integers must be an integer then it will be closed under addition.
Example
2 + 3 = 5
2+ (-3) = -1
(-2) + 3 = 1
(-2) + (-3) = -5
As you can see that the addition of two integers will always be an integer, hence integers are closed under addition.
If we have two integers p and q, p + q is an integer.
2. Closure under Subtraction
If the difference between two integers is also an integer then it is said to be closed under subtraction.
Example
7 – 2 = 5
7 – (- 2) = 9
- 7 – 2 = – 9
- 7 – (- 2) = – 5
As you can see that the subtraction of two integers will always be an integer, hence integers are closed under subtraction.
For any two integers p and q, p - q is an integer.
3. Commutative Property
(a) If we change the order of the integers while adding then also the result is the same then it is said that addition is commutative for integers.
For any two integers p and q
p + q = q + p
Example
23 + (-30) = – 7
(-30) + 23 = – 7
There is no difference in answer after changing the order of the numbers.
(b) If we change the order of the integers while subtracting then the result is not the same so subtraction is not commutative for integers.
For any two integers p and q
p – q ≠ q – p will not always equal.
Example
23 - (-30) = 53
(-30) - 23 = -53
The answer is different after changing the order of the numbers.
4. Associative Property
If we change the grouping of the integers while adding in case of more than two integers and the result is same then we will call it that addition is associative for integers.
For any three integers, p, q and r
Example
If there are three integers 3, 4 and 1 and we change the grouping of numbers, then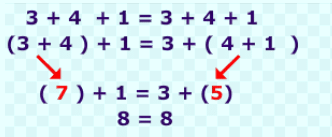
The result remains the same. Hence, addition is associative for integers.
5. Additive Identity
If we add zero to an integer, we get the same integer as the answer. So zero is an additive identity for integers.
For any integer p,
p + 0 = 0 + p =p
Example
2 + 0 = 2
(-7) + 0 = (-7)
Multiplication of Integers
Multiplication of two integers is the repeated addition.
Example
- 3 × (-2) = three times (-2) = (-2) + (-2) + (-2) = – 6
- 3 × 2 = three times 2 = 2 + 2 + 2 = 6
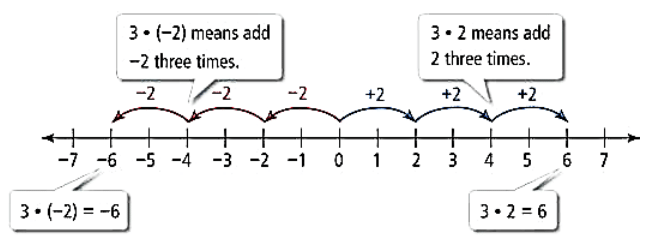
Now let’s see how to do the multiplication of integers without the number line.
1. Multiplication of a Positive Integer and a Negative Integer
To multiply a positive integer with a negative integer, we can multiply them as a whole number and then put the negative sign before their product.
So the product of a negative and a positive integer will always be a negative integer.
For two integers p and q,
p × (-q) = (-p) × q = - (p × q) = - pq
Example
4 × (-10) = (- 4) × 10 = - (4 × 10) = - 40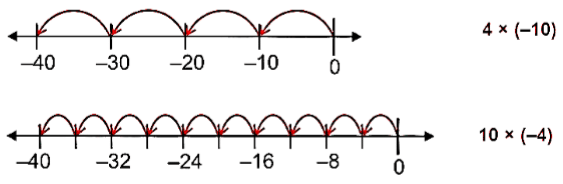
2. Multiplication of Two Negative Integers
To multiply two negative integers, we can multiply them as a whole number and then put the positive sign before their product.
Hence, if we multiply two negative integers then the result will always be a positive integer.
For two integers p and q,
(-p) × (-q) = (-p) × (-q) = p × q
Example
(-10) × (-3) = 30
3. The Product of Three or More Negative Integers
It depends upon the number of negative integers.
(a) If we multiply two negative integers then their product will be positive integer
(-3) × (-7) = 21
(b) If we multiply three negative integers then their product will be negative integer
(-3) × (-7) × (-10) = -210
If we multiply four negative integers then their product will be positive integer
(-3) × (-7) × (-10) × (-2) = 420
Hence, if the number of negative integers is even then the result will be a positive integer and if the number of negative integers is odd then the result will be a negative integer.
Properties of Multiplication of Integers
1. Closure under Multiplication
In case of multiplication, the product of two integers is always integer so integers are closed under multiplication.
For all the integers p and q
p×q = r, where r is an integer
Example
(-10) × (-3) = 30
(12) × (-4) = -48
2. Commutativity of Multiplication
If we change the order of the integers while multiplying then also the result will remain the same then it is said that multiplication is commutative for integers.
For any two integers p and q
p × q = q × p
Example
20 × (-30) = – 600
(-30) × 20 = – 600
There is no difference in answer after changing the order of the numbers.
3. Multiplication by Zero
If we multiply an integer with zero then the result will always be zero.
For any integer p,
p × 0 = 0 × p = 0
Example
9 × 0 = 0 × 9 = 0
0 × (-15) = 0
4. Multiplicative Identity
If we multiply an integer with 1 then the result will always the same as the integer.
For any integer q
q × 1 = 1 × q = q
Example
21 × 1 = 1 × 21 = 21
1 × (-15) = (-15)
5. Associative Property
If we change the grouping of the integers while multiplying in case of more than two integers and the result remains the same then it is said the associative property for multiplication of integers.
For any three integers, p, q and r
p × (q × r) = (p × q) × r
Example
If there are three integers 2, 3 and 4 and we change the grouping of numbers, then
The result remains the same. Hence, multiplication is associative for integers.
6. Distributive Property
(a) Distributivity of Multiplication over Addition.
For any integers a, b and c
a × (b + c) = (a × b) + (a × c)
Example
Solve the following by distributive property.
I. 35 × (10 + 2) = 35 × 10 + 35 × 2
= 350 + 70
= 420
II. (– 4) × [(–2) + 7] = (– 4) × 5 = – 20 And
= [(– 4) × (–2)] + [(– 4) × 7]
= 8 + (–28)
= –20
So, (– 4) × [(–2) + 7] = [(– 4) × (–2)] + [(– 4) × 7]
(b) Distributivity of multiplication over subtraction
For any integers a, b and c
a × (b – c) = (a × b) – (a × c)
Example
5 × (3 – 8) = 5 × (- 5) = – 25
5 × 3 – 5 × 8 = 15 – 40 = – 25
So, 4 × (3 – 8) = 4 × 3 – 4 × 8.
Division of integers
1. Division of a Negative Integer by a Positive Integer
The division is the inverse of multiplication. So, like multiplication, we can divide them as a whole number and then place a negative sign prior to the result. Hence the answer will be in the form of a negative integer.
For any integers p and q,
(– p) ÷ q = p ÷ (- q) = - (p ÷ q) where, q ≠ 0
Example
64 ÷ (- 8) = – 8
2. Division of Two Negative Integers
To divide two negative integers, we can divide them as a whole number and then put the positive sign before the result.
The division of two negative integers will always be a positive integer.
For two integers p and q,
(- p) ÷ (- q) = (-p) ÷ (- q) = p ÷ q where q ≠ 0
Example
(-10) ÷ (- 2) = 5
Properties of Division of Integers
For any integers p, q and r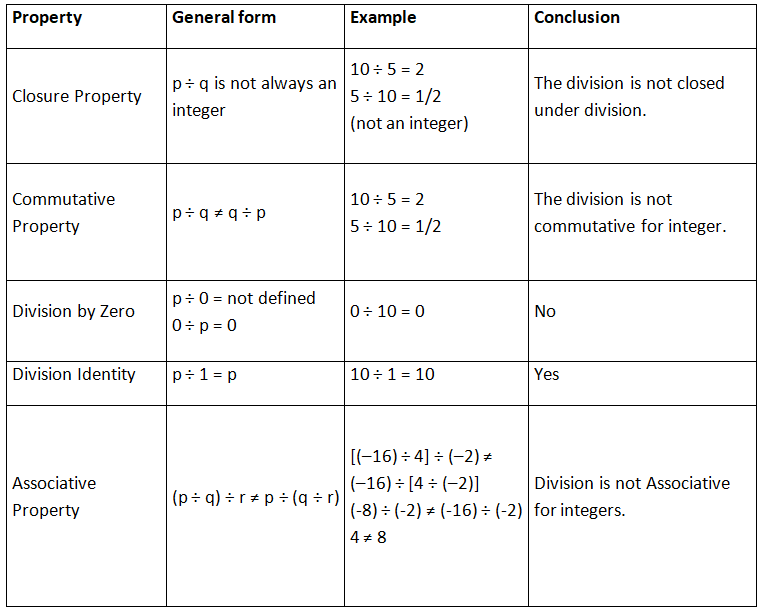
|
28 videos|76 docs|22 tests
|
FAQs on Integers Class 7 Notes Maths Chapter 1
| 1. How do you add and subtract integers on the number line? |  |
| 2. What is the additive inverse of an integer? |  |
| 3. What are the properties of addition and subtraction of integers? |  |
| 4. How do you multiply integers? |  |
| 5. What are the properties of multiplication of integers? |  |

















