Class 8 Exam > Class 8 Notes > Mathematics (Maths) Class 8 > Points to Remember: Mensuration
Points to Remember: Mensuration | Mathematics (Maths) Class 8 PDF Download
Important Formulae
1. Area of a parallelogram = Base * Height
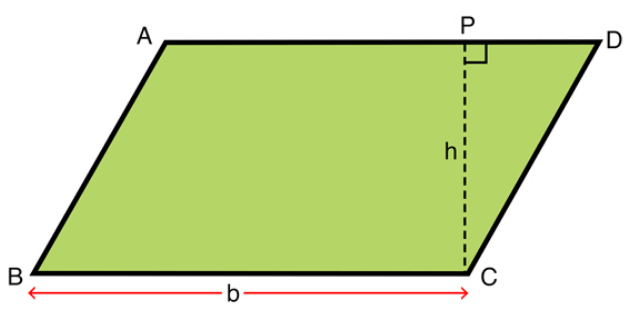
2. Area of a triangle = 1/2 * Base * Height
3. Area of a trapezium = 1/2 * [Sum of parallel sides] * Height
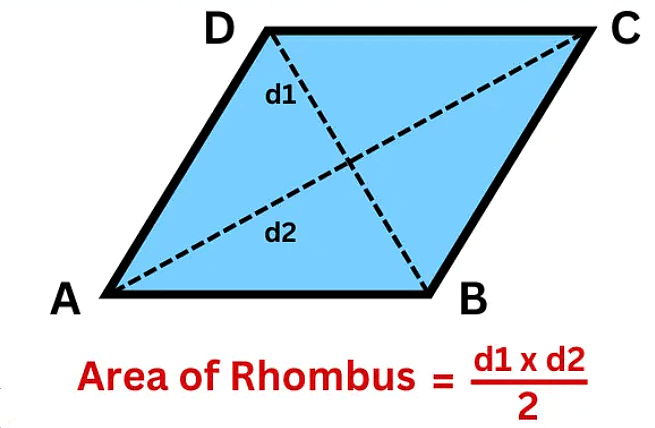
4. Area of a rhombus = 1/2 * Product of diagonals
5. Surface area of
(i) a cuboid = 2[lb + bh + hl]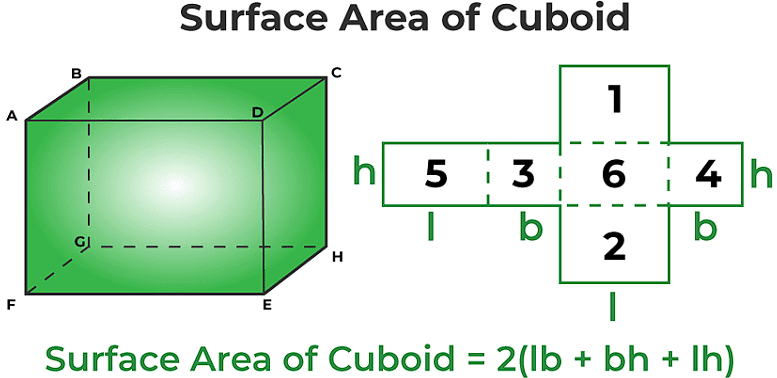
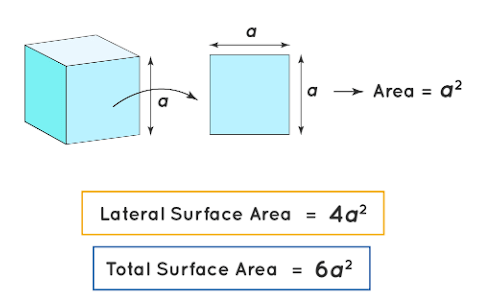
(ii) a cube = 6a2
(iii) a cylinder = 2πr(r + h)
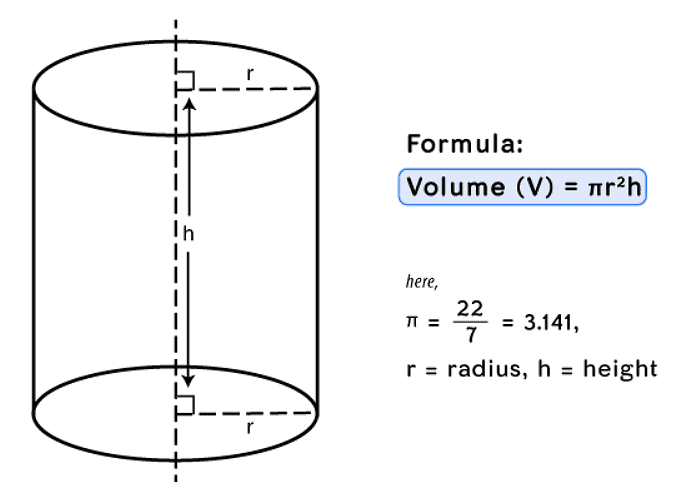
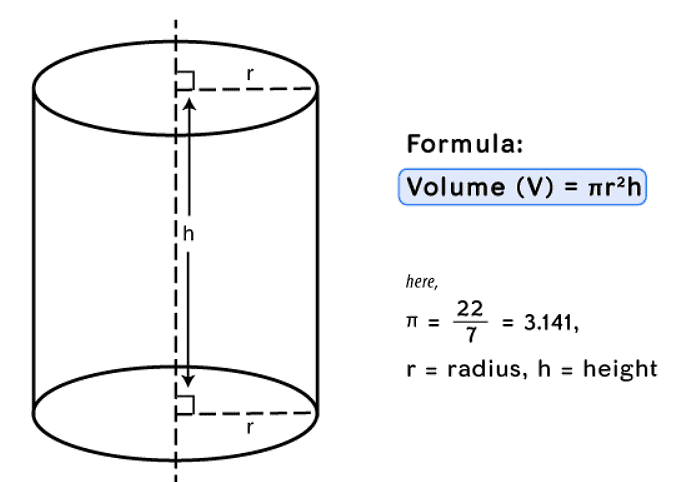
6. Volume of
(i) cuboid = l * b * h
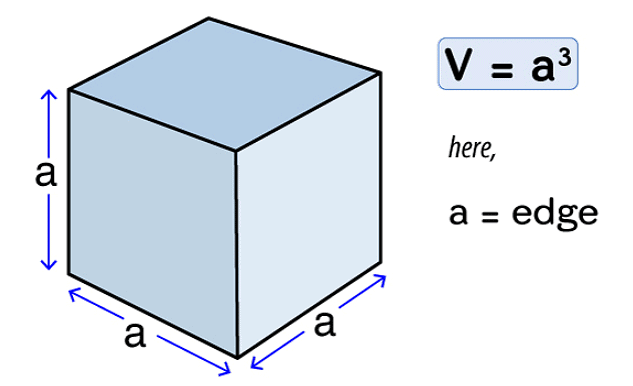
(ii) cube = l3
(iii) cylinder = πr2h
- 1 m3 = 1000 litres
- A square, a rectangle, a trapezium, a rhombus, a parallelogram, a triangle, a circle, etc., are plane figures and the surfaces enclosed by their boundaries are called areas. We have formulae to find their areas. The perimeter is the distance around a figure. The plane figures are also called 2-D shapes. The solids such as cubes, cuboids, cylinders are called 3-D shapes. A 3-D shape is bounded by faces. These faces can be rectilinear or curved or both.
- We also know that:
(i) The area of a square = Side * Side
(ii) The area of a rectangle = Length * Breadth
(iii) The area of a circle = πr2 [where r is the radius]
(iv) The area of triangle = 1/2 * Base * Altitude
(v) The area of a parallelogram = Base * Height
Note:
I. All angles of a regular polygon have equal degree measures.
II. All sides of a regular polygon are equal in length.
Solved Examples
Q1. The length and breadth of a rectangle are 10 cm and 8 cm respectively. Find its perimeter if the length and breadth are (i) doubled (ii) halved..
Ans:
Length of the rectangle = 10 cm
Breadth of the rectangle = 8 cm
(i) When they are doubled,
l = 10 × 2 = 20 cm
and b = 8 × 2 = 16 cm
Perimeter = 2(l + b) = 2(20 + 16) = 2 × 36 = 72 cm
(ii) When they are halved,
l = 10/2 = 5 cm
b = 8/2 = 4 cm
Perimeter = 2(l + b) = 2(5 + 4) = 2 × 9 = 18 cmQuestion for Points to Remember: MensurationTry yourself:Q2. If the lateral surface of the cylinder is 500 cm² and its height is 10 cm, then find the radius of its base.
View Solution
Q2. A horse is tethered by a rope 10 m long at a point. Find the area of the region where it can graze (π = 3.14)
Solution: The area of the region the horse can graze is circular with a radius equal to the length of the rope.
The area of the circle is given by πr²
= 3.14 × 10²
= 3.14 × 100
=314
Hence the area of the region the horse can graze is 314 cm².
The document Points to Remember: Mensuration | Mathematics (Maths) Class 8 is a part of the Class 8 Course Mathematics (Maths) Class 8.
All you need of Class 8 at this link: Class 8
|
79 videos|408 docs|31 tests
|
FAQs on Points to Remember: Mensuration - Mathematics (Maths) Class 8
| 1. What are the basic formulae for calculating the area and perimeter of common shapes in mensuration? |  |
Ans.The basic formulae for calculating area and perimeter are as follows:
- Rectangle: Area = Length × Breadth; Perimeter = 2(Length + Breadth)
- Square: Area = Side × Side; Perimeter = 4 × Side
- Triangle: Area = (Base × Height) / 2; Perimeter = Sum of all sides
- Circle: Area = π × Radius²; Circumference (perimeter) = 2π × Radius.
| 2. How do you calculate the volume of 3D shapes like cubes and cylinders in mensuration? | |
Ans.The volume of common 3D shapes can be calculated using these formulas:
- Cube: Volume = Side³
- Rectangular Prism: Volume = Length × Breadth × Height
- Cylinder: Volume = π × Radius² × Height
- Cone: Volume = (1/3) × π × Radius² × Height.
| 3. What is the difference between area and volume in mensuration? | |
Ans.Area measures the space inside a two-dimensional shape (like squares, rectangles, etc.) and is expressed in square units (e.g., cm², m²). Volume measures the space inside a three-dimensional object (like cubes, cylinders, etc.) and is expressed in cubic units (e.g., cm³, m³).
| 4. How can I apply mensuration formulas in real-life situations? | |
Ans.Mensuration formulas are used in various real-life situations, such as:
- Calculating the amount of paint needed for a wall (area).
- Determining the volume of water a tank can hold (volume).
- Estimating land area for agriculture or construction (area).
- Designing packaging for products (volume of boxes).
| 5. Are there any tips for solving mensuration problems quickly and accurately? | |
Ans.Yes, here are some tips:
- Familiarize yourself with the key formulas for different shapes.
- Draw diagrams to visualize the problem whenever possible.
- Break complex problems into smaller, manageable parts.
- Practice regularly to improve speed and accuracy.
- Double-check your calculations to avoid simple mistakes.
Related Exams
About this Document
|
11.3K Views |
|
4.92/5 Rating |
|
Nov 21, 2024 Last updated |
Document Description: Points to Remember: Mensuration for Class 8 2024 is part of Mathematics (Maths) Class 8 preparation.
The notes and questions for Points to Remember: Mensuration have been prepared according to the Class 8 exam syllabus. Information about Points to Remember: Mensuration covers topics
like Important Formulae, Solved Examples and Points to Remember: Mensuration Example, for Class 8 2024 Exam. Find important definitions, questions, notes, meanings, examples, exercises and tests below for Points to Remember: Mensuration.
Introduction of Points to Remember: Mensuration in English is available as part of our Mathematics (Maths) Class 8
for Class 8 & Points to Remember: Mensuration in Hindi for Mathematics (Maths) Class 8 course.
Download more important topics related with notes, lectures and mock test series for Class 8
Exam by signing up for free. Class 8: Points to Remember: Mensuration | Mathematics (Maths) Class 8
Description
Full syllabus notes, lecture & questions for Points to Remember: Mensuration | Mathematics (Maths) Class 8 - Class 8 | Plus excerises question with solution to help you revise complete syllabus for Mathematics (Maths) Class 8 | Best notes, free PDF download
Information about Points to Remember: Mensuration
In this doc you can find the meaning of Points to Remember: Mensuration defined & explained in the simplest way possible. Besides explaining types of
Points to Remember: Mensuration theory, EduRev gives you an ample number of questions to practice Points to Remember: Mensuration tests, examples and also practice Class 8
tests
|
Explore Courses for Class 8 exam
|
|
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.
Related Searches
practice quizzes
,Points to Remember: Mensuration | Mathematics (Maths) Class 8
,Extra Questions
,mock tests for examination
,Semester Notes
,past year papers
,study material
,Free
,Points to Remember: Mensuration | Mathematics (Maths) Class 8
,Exam
,video lectures
,ppt
,Points to Remember: Mensuration | Mathematics (Maths) Class 8
,Previous Year Questions with Solutions
,Objective type Questions
,Viva Questions
,Important questions
,Sample Paper
,shortcuts and tricks
,MCQs
,Summary
;
Additional Information about Points to Remember: Mensuration for Class 8 Preparation
Points to Remember: Mensuration Free PDF Download
The Points to Remember: Mensuration is an invaluable resource that delves deep into the core of the Class 8 exam.
These study notes are curated by experts and cover all the essential topics and concepts, making your preparation more efficient and effective.
With the help of these notes, you can grasp complex subjects quickly, revise important points easily,
and reinforce your understanding of key concepts. The study notes are presented in a concise and easy-to-understand manner,
allowing you to optimize your learning process. Whether you're looking for best-recommended books, sample papers, study material,
or toppers' notes, this PDF has got you covered. Download the Points to Remember: Mensuration now and kickstart your journey towards success in the Class 8 exam.
Importance of Points to Remember: Mensuration
The importance of Points to Remember: Mensuration cannot be overstated, especially for Class 8 aspirants.
This document holds the key to success in the Class 8 exam.
It offers a detailed understanding of the concept, providing invaluable insights into the topic.
By knowing the concepts well in advance, students can plan their preparation effectively.
Utilize this indispensable guide for a well-rounded preparation and achieve your desired results.
Points to Remember: Mensuration Notes
Points to Remember: Mensuration Notes offer in-depth insights into the specific topic to help you master it with ease.
This comprehensive document covers all aspects related to Points to Remember: Mensuration.
It includes detailed information about the exam syllabus, recommended books, and study materials for a well-rounded preparation.
Practice papers and question papers enable you to assess your progress effectively.
Additionally, the paper analysis provides valuable tips for tackling the exam strategically.
Access to Toppers' notes gives you an edge in understanding complex concepts.
Whether you're a beginner or aiming for advanced proficiency, Points to Remember: Mensuration Notes on EduRev are your ultimate resource for success.
Points to Remember: Mensuration Class 8 Questions
The "Points to Remember: Mensuration Class 8 Questions" guide is a valuable resource for all aspiring students preparing for the
Class 8 exam. It focuses on providing a wide range of practice questions to help students gauge
their understanding of the exam topics. These questions cover the entire syllabus, ensuring comprehensive preparation.
The guide includes previous years' question papers for students to familiarize themselves with the exam's format and difficulty level.
Additionally, it offers subject-specific question banks, allowing students to focus on weak areas and improve their performance.
Study Points to Remember: Mensuration on the App
Students of Class 8 can study Points to Remember: Mensuration alongwith tests & analysis from the EduRev app,
which will help them while preparing for their exam. Apart from the Points to Remember: Mensuration,
students can also utilize the EduRev App for other study materials such as previous year question papers, syllabus, important questions, etc.
The EduRev App will make your learning easier as you can access it from anywhere you want.
The content of Points to Remember: Mensuration is prepared as per the latest Class 8 syllabus.
|
© EduRev
|
Education Revolution
|
Follow Us
|
Signup on EduRev and stay on top of your study goals
10M+ students crushing their study goals daily