Class 8 Exam > Class 8 Notes > Mathematics (Maths) Class 8 > Points to Remember: Understanding Quadrilaterals
Points to Remember: Understanding Quadrilaterals | Mathematics (Maths) Class 8 PDF Download
| Table of contents |
|
| Polygon |
|
| Concave polygons |
|
| Convex polygons |
|
| Regular and irregular polygons |
|
| Parallelogram |
|
| Rhombus |
|
| Rectangle |
|
| Square |
|
| Kite |
|
| Trapezium |
|
| Diagonal |
|
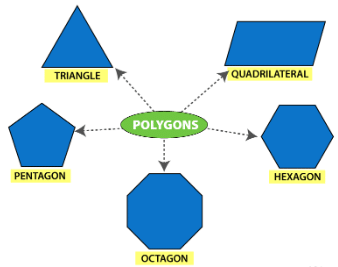
Polygon
A simple closed curve made up of only line segments is called a polygon.
Concave polygons
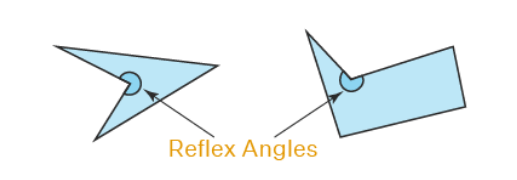
Convex polygons
A polygon is a two-dimensional shape that has a minimum of three sides and angles. A convex polygon is a shape in which all of its vertices point in the outward direction.
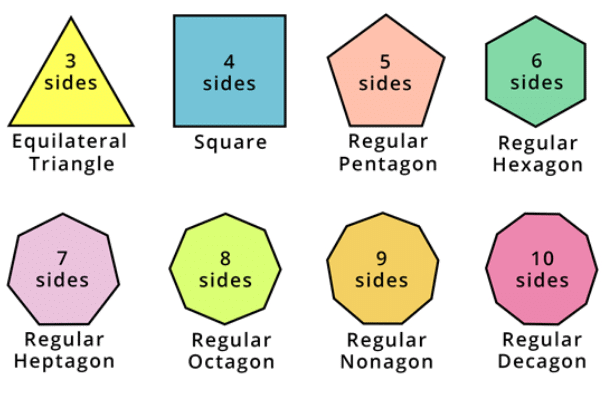
Regular and irregular polygons
A regular polygon is a two-dimensional shape having all sides of equal length and all interior angles of equal measure.
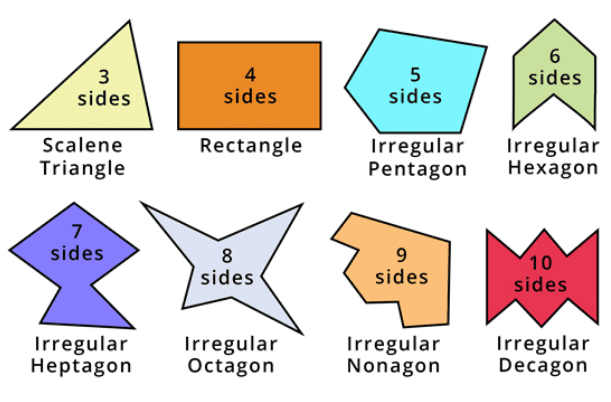
An irregular polygon, also known as non-regular polygon is a shape that does not have all sides of equal length and all angles of equal.
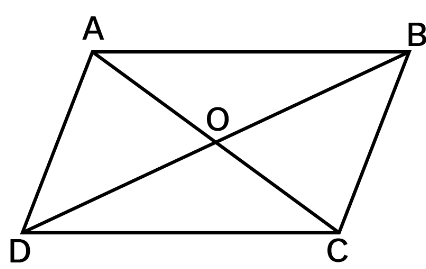
Parallelogram
A quadrilateral with each pair of opposite sides parallel.
- Opposite sides are equal.
- Opposite angles are equal.
- Diagonals bisect one another.
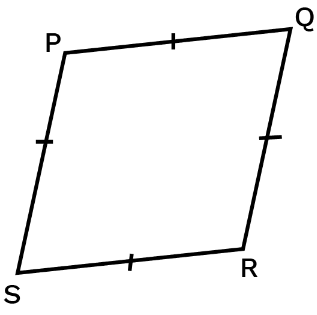
Rhombus
A parallelogram with sides of equal length.
- All the properties of a parallelogram.
- Diagonals are perpendicular to each other.
Rectangle
A parallelogram with a right angle.
- All the properties of a parallelogram.
- Each of the angles is a right angle.
- Diagonals are equal.
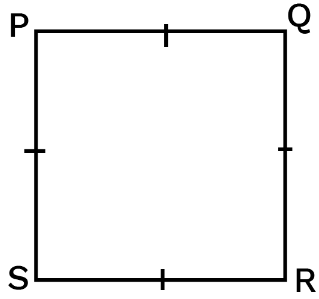
Square
- A rectangle with sides of equal length.
- All the properties of a parallelogram, rhombus, and a rectangle.
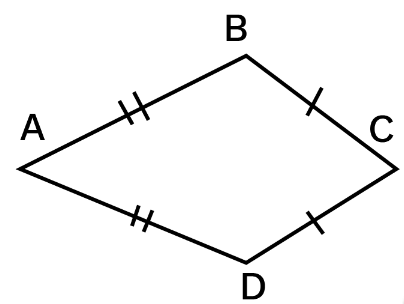
Kite
A quadrilateral with exactly two pairs of equal consecutive sides.
- The diagonals are perpendicular to one another.
- One of the diagonals bisects the other.
- From figure, m∠B=m∠D but m∠A≠m∠C
Trapezium
A quadrilateral having exactly one pair of parallel sides.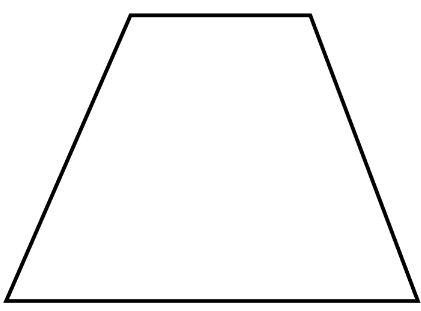
Diagonal
- A simple closed curve is made up of only line segments.
- A line segment connecting two non-consecutive vertices of a polygon is called diagonal.
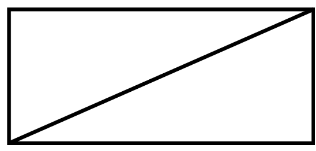
Convex: The measure of each angle is less than 180º .
Concave: The measure of at least one angle is more than 180º.
Quadrilateral: A polygon having four sides.
Element of quadrilateral:
(i) Sides: Line segments joining the points.
(ii) Vertices: Point of intersection of two consecutive sides.
(iii) Opposite sides: Two sides of a quadrilateral having no common endpoint.
(iv) Opposite Angles: Two angles of a quadrilateral not having a common arm.
(v) Diagonals: A line segment is obtained by joining the opposite vertices.
(vi) Adjacent Angles: Two angles of a quadrilateral having a common arm.
(vii) Adjacent Sides: Two sides of a quadrilateral having a common endpoint.
The document Points to Remember: Understanding Quadrilaterals | Mathematics (Maths) Class 8 is a part of the Class 8 Course Mathematics (Maths) Class 8.
All you need of Class 8 at this link: Class 8
|
79 videos|408 docs|31 tests
|
FAQs on Points to Remember: Understanding Quadrilaterals - Mathematics (Maths) Class 8
| 1. What are the different types of quadrilaterals? |  |
Ans. The different types of quadrilaterals are parallelogram, rectangle, square, rhombus, trapezium, and kite.
| 2. How do you identify a quadrilateral? | |
Ans. A quadrilateral is a polygon with four sides and four angles. It can be identified by counting the number of sides and angles in a shape.
| 3. What is the sum of the interior angles of a quadrilateral? | |
Ans. The sum of the interior angles of a quadrilateral is always 360 degrees.
| 4. How do you classify a quadrilateral based on its sides and angles? | |
Ans. A quadrilateral can be classified as regular or irregular based on its sides and angles. Regular quadrilaterals have equal sides and angles, while irregular quadrilaterals have different sides and angles.
| 5. Can a quadrilateral have all right angles? | |
Ans. Yes, a quadrilateral with all right angles is called a rectangle.
Related Exams
About this Document
|
5.3K Views |
|
4.67/5 Rating |
|
Dec 24, 2024 Last updated |
Document Description: Points to Remember: Understanding Quadrilaterals for Class 8 2024 is part of Mathematics (Maths) Class 8 preparation.
The notes and questions for Points to Remember: Understanding Quadrilaterals have been prepared according to the Class 8 exam syllabus. Information about Points to Remember: Understanding Quadrilaterals covers topics
like Polygon , Concave polygons , Convex polygons, Regular and irregular polygons, Parallelogram, Rhombus, Rectangle, Square, Kite, Trapezium, Diagonal and Points to Remember: Understanding Quadrilaterals Example, for Class 8 2024 Exam. Find important definitions, questions, notes, meanings, examples, exercises and tests below for Points to Remember: Understanding Quadrilaterals.
Introduction of Points to Remember: Understanding Quadrilaterals in English is available as part of our Mathematics (Maths) Class 8
for Class 8 & Points to Remember: Understanding Quadrilaterals in Hindi for Mathematics (Maths) Class 8 course.
Download more important topics related with notes, lectures and mock test series for Class 8
Exam by signing up for free. Class 8: Points to Remember: Understanding Quadrilaterals | Mathematics (Maths) Class 8
Description
Full syllabus notes, lecture & questions for Points to Remember: Understanding Quadrilaterals | Mathematics (Maths) Class 8 - Class 8 | Plus excerises question with solution to help you revise complete syllabus for Mathematics (Maths) Class 8 | Best notes, free PDF download
Information about Points to Remember: Understanding Quadrilaterals
In this doc you can find the meaning of Points to Remember: Understanding Quadrilaterals defined & explained in the simplest way possible. Besides explaining types of
Points to Remember: Understanding Quadrilaterals theory, EduRev gives you an ample number of questions to practice Points to Remember: Understanding Quadrilaterals tests, examples and also practice Class 8
tests
|
Explore Courses for Class 8 exam
|
|
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.
Related Searches
Free
,Previous Year Questions with Solutions
,Sample Paper
,Semester Notes
,study material
,Objective type Questions
,Extra Questions
,MCQs
,practice quizzes
,Points to Remember: Understanding Quadrilaterals | Mathematics (Maths) Class 8
,Important questions
,video lectures
,shortcuts and tricks
,Points to Remember: Understanding Quadrilaterals | Mathematics (Maths) Class 8
,Points to Remember: Understanding Quadrilaterals | Mathematics (Maths) Class 8
,past year papers
,ppt
,mock tests for examination
,Summary
,Exam
,Viva Questions
;
Additional Information about Points to Remember: Understanding Quadrilaterals for Class 8 Preparation
Points to Remember: Understanding Quadrilaterals Free PDF Download
The Points to Remember: Understanding Quadrilaterals is an invaluable resource that delves deep into the core of the Class 8 exam.
These study notes are curated by experts and cover all the essential topics and concepts, making your preparation more efficient and effective.
With the help of these notes, you can grasp complex subjects quickly, revise important points easily,
and reinforce your understanding of key concepts. The study notes are presented in a concise and easy-to-understand manner,
allowing you to optimize your learning process. Whether you're looking for best-recommended books, sample papers, study material,
or toppers' notes, this PDF has got you covered. Download the Points to Remember: Understanding Quadrilaterals now and kickstart your journey towards success in the Class 8 exam.
Importance of Points to Remember: Understanding Quadrilaterals
The importance of Points to Remember: Understanding Quadrilaterals cannot be overstated, especially for Class 8 aspirants.
This document holds the key to success in the Class 8 exam.
It offers a detailed understanding of the concept, providing invaluable insights into the topic.
By knowing the concepts well in advance, students can plan their preparation effectively.
Utilize this indispensable guide for a well-rounded preparation and achieve your desired results.
Points to Remember: Understanding Quadrilaterals Notes
Points to Remember: Understanding Quadrilaterals Notes offer in-depth insights into the specific topic to help you master it with ease.
This comprehensive document covers all aspects related to Points to Remember: Understanding Quadrilaterals.
It includes detailed information about the exam syllabus, recommended books, and study materials for a well-rounded preparation.
Practice papers and question papers enable you to assess your progress effectively.
Additionally, the paper analysis provides valuable tips for tackling the exam strategically.
Access to Toppers' notes gives you an edge in understanding complex concepts.
Whether you're a beginner or aiming for advanced proficiency, Points to Remember: Understanding Quadrilaterals Notes on EduRev are your ultimate resource for success.
Points to Remember: Understanding Quadrilaterals Class 8 Questions
The "Points to Remember: Understanding Quadrilaterals Class 8 Questions" guide is a valuable resource for all aspiring students preparing for the
Class 8 exam. It focuses on providing a wide range of practice questions to help students gauge
their understanding of the exam topics. These questions cover the entire syllabus, ensuring comprehensive preparation.
The guide includes previous years' question papers for students to familiarize themselves with the exam's format and difficulty level.
Additionally, it offers subject-specific question banks, allowing students to focus on weak areas and improve their performance.
Study Points to Remember: Understanding Quadrilaterals on the App
Students of Class 8 can study Points to Remember: Understanding Quadrilaterals alongwith tests & analysis from the EduRev app,
which will help them while preparing for their exam. Apart from the Points to Remember: Understanding Quadrilaterals,
students can also utilize the EduRev App for other study materials such as previous year question papers, syllabus, important questions, etc.
The EduRev App will make your learning easier as you can access it from anywhere you want.
The content of Points to Remember: Understanding Quadrilaterals is prepared as per the latest Class 8 syllabus.
|
© EduRev
|
Education Revolution
|
|
Signup to see your scores
go up within 7 days!
Access 1000+ FREE Docs, Videos and Tests
Takes less than 10 seconds to signup