Short Notes for Hydrostatic Forces | Short Notes for Civil Engineering - Civil Engineering (CE) PDF Download
What is Hydrostatic Force?
Hydrostatic force is the force exerted by the static fluid on any object placed into it. It depends on the depth of the object from the free surface. Hydrostatic force for vertical and inclined surfaces will be different for horizontal surfaces. This topic comes under the fluid statics part.
Fundamental concepts in fluid mechanics include calculating the hydrostatic force and the location of the centre of pressure. A location on the submerged surface where the hydrostatic pressure acts is known as the centre of pressure.
Definition of Hydrostatic Force
The resultant force created by a liquid’s pressure loading acting on submerged surfaces is known as hydrostatic force.
When a surface is immersed in a fluid, the fluid’s forces act on the surface. These forces must be determined for designing storage tanks, ships, dams, and other hydraulic structures. Since there are no shearing stresses in place for fluids at rest, we know that the force must be perpendicular to the surface. If the fluid is incompressible, the pressure changes linearly with depth.
Fluid Statics
- Fluid Statics deals with fluids at rest, while Fluid Dynamics studies fluids in motion.
- Any force developed is only due to normal stresses, i.e., pressure. Such a condition is termed the hydrostatic condition.
- Fluid Statics is also known as Hydrostatics.
- A static fluid can have no shearing force acting on it, and any force between the fluid and the boundary must be acting at right angles to the boundary.
- The element will be in equilibrium for an element of fluid at rest. The sum of the components of forces in any direction will be zero. The sum of the moments of forces on the element about any point must also be zero.
- Within a fluid, the pressure is the same at all points in all directions.
- Pressure at the wall of any vessel is perpendicular to the wall
- Pressure due to depth is P = ρgh and is the same at any horizontal level of connected fluid.
Fluid Pressure at a Point
- If a fluid is Stationary, then force acting on any surface or area is perpendicular to that surface.
- If the force exerted on each unit area of a boundary is the same, the pressure is said to be uniform.
Hydrostatic Force Formula
Hydrostatic forces result from a liquid’s pressure loading acting on submerged surfaces. The total hydrostatic force for a horizontal plane surface submerged in liquid, a plane surface inside of a gas chamber, or any other plane surface subject to the influence of uniform hydrostatic pressure is given by:
F = pA
where A is the area and p is the uniform pressure.
Pascal’s Law for Pressure At A Point
It states that pressure or intensity of pressure at a point in a static fluid (fluid is at rest) is equal in all directions. If the fluid is not in motion, then according to Pascal’s law,
px = py = pz
where px, py and pz are the pressure at points x,y, and z, respectively.
General Equation For Variation Of Pressure in a Static Fluid
According to Pascal’s law, fluid pressure will be constant at all points of a horizontal surface. The variation of hydrostatic force will occur for the inclined surface and for the vertical surface. And this variation will happen along the depth of the surface from the free surface.
Vertical Variation of Pressure in a Fluid Under Gravity
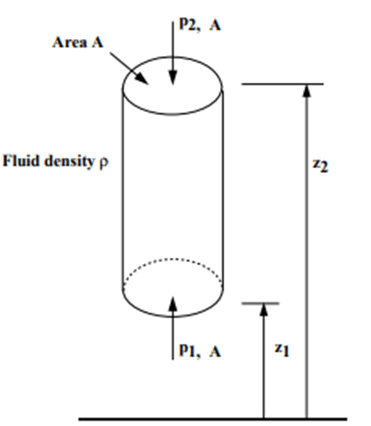
Taking upward as a positive, we have
Vertical cylindrical element of fluid cross-sectional area = A
mass density = ρ
The forces involved are:
- Force due to p1 on A (upward) = p1. A
- Force due to p2 on A (downward) = p2. A
- Force due to weight of element (downward) = mg
= mass density x volume x g
= ρ.g.A.(z2 – z1)
Thus in a fluid under gravity, pressure decreases linearly with an increase in height.
p2 – p1 = ρgA(z2 – z1 )
This is the hydrostatic pressure change.
Equality of Pressure At The Same Level In A Static Fluid
As we know Pascal’s law, so it can be understood that the hydrostatic pressure at the horizontal surface is the same at all points. And pressure intensity will be uniform.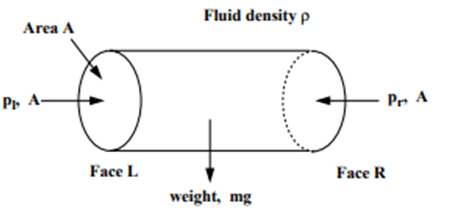
Horizontal cylindrical element cross-sectional area = A
mass density =ρ
left end pressure = pl
right end pressure = pr
For equilibrium, the sum of the forces in the x-direction is zero= pl. A = pr. A
pl = pr
So, Pressure in the horizontal direction is constant.
Total Hydrostatic Force on Plane Surfaces
The hydrostatic force depends on the type of surface, whether horizontal, vertical or inclined. Here the calculation of hydrostatic forces for different types of surfaces and flow conditions are explained below.
- For a horizontal plane, surface submerged in liquid, plane surface inside a gas chamber, or any plane surface under the action of uniform hydrostatic pressure, the total hydrostatic force is given by
F = p. A
where p is the uniform pressure and A is the area.
- In general, the total hydrostatic pressure on any plane surface is equal to the product of the area of the surface and the unit pressure at its centre of gravity.
F = pcg. A
where pcg is the pressure at the centre of gravity.
- For homogeneous, free liquid at rest, the equation can be expressed in terms of the unit weight γ of the liquid.
F=γh’A
- where h’ is the depth of liquid above the centroid of the submerged area.
Derivation of Formulas
The figure shown below is an inclined plane surface submerged in a liquid. The total area of the plane surface is given by A, cg is the centre of gravity, and cp is the centre of pressure.
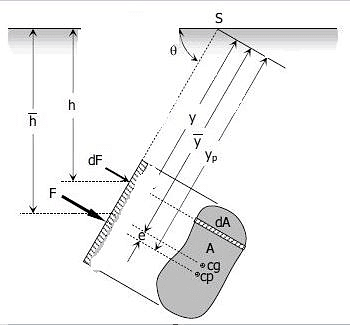
(Forces on an inclined plane surface)
The differential force dF acting on the element dA is
dF=p. dA
dF=γ. h. dA
From the figure
h=ysinθ,
dF=γ.(ysinθ). dA
Integrate both sides and note that γ and θ are constants,
F=γ. sinθ. ∫y.dA
So, F=γ. sinθ. ∫y.dA
Recall from Calculus that
∫y.dA=A.y¯
Hence, F=(γ.sinθ)A.y¯
F=γ. (y¯sinθ). A
From the figure, y¯sinθ=h¯, thus,
F = γh¯A
The product γh¯¯ is a unit pressure at the centroid at the plane area; thus, the formula can be expressed in a more general term below:
F = pcg. A
Location of Total Hydrostatic Force (Eccentricity)
From the figure above, S is the intersection of the prolongation of the submerged area to the free liquid surface. Taking a moment about point S.
Fyp=∫y. dF
Where
dF=γ(ysinθ)dA
F=γ(y¯sinθ)A
[γ(y¯sinθ)A]yp =∫y[γ(ysinθ)dA][γ(y¯sinθ)A]yp
=∫y[γ(ysinθ)dA]
(γsinθ)Ay¯yp=(γsinθ)∫y2dA(γsinθ)Ay¯yp
=(γsinθ)∫y2dA
Ay¯yp=∫y2dA
Again from Calculus, ∫y2dA is the moment of inertia denoted by I. Since our reference point is S,
Ay¯yp=IS
Thus,
yp =IS/Ay¯
By transfer formula for the moment of inertia IS=Ig+Ay¯2, the formula for yp will become
yp=(Ig+Ay¯2)/Ay¯ or
yp=y¯+Ig/Ay¯
From the figure above, yp=y¯+e; thus, the distance between CG and CP is
Eccentricity, e=Ig/Ay¯
Applications of Hydrostatic Force
he concept of hydrostatic force has many applications in real life. For example, lifting a hydraulic jack can be easily possible with hydrostatic force; this principle is commonly used at the car washing centre. Here a few applications of hydrostatic force are listed below.
- Opening the gate of a Dam.
- Lifting of hydraulic jack
- Designing the hydraulic structures
Total Hydrostatic Force on Curved Surfaces
Force on a curved surface can be calculated by splitting it into verticle surfaces and horizontal surfaces. Here the different cases of hydrostatic force on a curved surface are explained.
- In the case of a curved surface submerged in liquid at rest, it is more convenient to deal with the horizontal and vertical components of the total force acting on the surface. Note: the discussion here is also applicable to plane surfaces.
- Horizontal Component: The horizontal component of the total hydrostatic force on any surface is equal to the pressure on the vertical projection of that surface.
FH=pcg. A
Vertical Component, The vertical component of the total hydrostatic force on any surface is equal to the weight of either real or imaginary liquid above it.
FV=γ. V
- Total Hydrostatic Force
F=√(FH2+FV2)
- The direction of F
tanθx=FV/FH
Applications of Hydrostatic Force
There are various applications of hydrostatic force. This force provides various advantages because of its property. The structural design of water-control structures like dams, floodwalls, and gates is heavily influenced by the position and strength of the water pressure force pressing on those structures.
Many hydraulic equipment components must be designed following the principles of hydrostatic force and its course of action.
Important Points Related to Hydrostatic Force
The hydrostatic force exerted on the vertical surface of the quadrant when it is submerged by adding water to the tank can be calculated by taking into account the following:
- The hydrostatic force at any point on the curved surfaces is normal to the surface and resolves at the pivot point since it is positioned at the origin of the radii. Because the hydrostatic forces travel through the pivot, they have no net influence on the upper and lower curved surfaces and produce no torque that may change the assembly’s equilibrium.
- The forces on the quadrant’s sides are horizontal and balance one another out (equal and opposite)
- The balance weight balances the hydrostatic force on the vertical submerged face. Therefore, the value of the balance weight and the depth of the water can be used to compute the resulting hydrostatic force on the face.
- The system is in equilibrium if the moments produced by the hydrostatic force and added weight (mg) about the pivot points are equal, that is:
mg × L = F × y
Example of Hydrostatic Force
As was discussed, hydrostatic force is very important for the GATE and other competitive exams. So it is important to understand this topic with a better approach. A common example related to this topic is given that strengthens the related concepts.
Example: The length of a tainter gate is 1 m perpendicular to the plane of the paper. Find out the total horizontal force on the gate and hydrostatic force on the gate.
Sol: 

FAQs on Short Notes for Hydrostatic Forces - Short Notes for Civil Engineering - Civil Engineering (CE)
| 1. What is hydrostatic force? |  |
| 2. What is the formula for hydrostatic force? |  |
| 3. What is the general equation for the variation of pressure in a static fluid? |  |
| 4. Why is the pressure equal at the same level in a static fluid? |  |
| 5. How does hydrostatic force affect submerged objects? |  |

|
Explore Courses for Civil Engineering (CE) exam
|

|
















