Class 9 Maths Chapter 5 Question Answers - Introduction to Euclid’s Geometry
Q1:In the given figure, name the following :
(i) Four collinear points
(ii) Five rays
(iii) Five line segments
(iv) Two-pairs of non-intersecting line segments.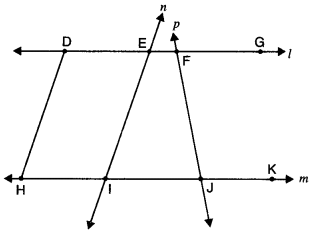 Ans:
Ans:
(i) Four collinear points are D, E, F, G and H, I, J, K
(ii) Five rays are DG, EG, FG, HK, IK.
(iii) Five line segments are DH, EI, FJ; DG, HK.
(iv) Two-pairs of non-intersecting line segments are (DH, EI) and (DG, HK).
Q2: In figure, it is given that AD=BC. By which Euclid’s axiom it can be proved that AC = BD? Ans:
Ans:
We can prove it by Euclid’s axiom 3. “If equals are subtracted from equals, the remainders are equal.”
We have AD = BC
⇒ AD – CD = BC – CD
⇒ AC = BD
Q3: In the beow figure, if AB = PQ, PQ = XY, then AB = XY. State True or False. Justify your answer. Ans:
Ans:
True.
∵ By Euclid’s first axiom “Things which are equal to the same thing are equal to one another”.
∴ AB = PQ and XY = PQ ⇒ AB = XY
Q4: In the given figure, AC = XD, C is mid-point of AB and D is mid-point of XY. Using an Euclid’s axiom, show that AB = XY.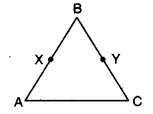 Ans:
Ans:
∵ C is the mid-point of AB
AB = 2AC
Also, D is the mid-point of XY
XY = 2XD
By Euclid’s sixth axiom “Things which are double of same things are equal to one another.”
∴ AC = XD = 2AC = 2XD
⇒ AB = XY
Q5: In the figure, we have BX and 1/2 AB = 1/2 BC. Show that BX = BY.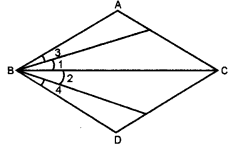 Ans:
Ans:
Here, BX = 1/2 AB and BY = 1/2 BC …(i) [given]
Also, AB = BC [given]
⇒ 1/2AB = 1/2BC …(ii)
[∵ Euclid’s seventh axiom says, things which are halves of the same thing are equal to one another]
From (i) and (ii), we have
BX = BY
Q6: In the given figure, if ∠1 = ∠3, ∠2 = ∠4 and ∠3 = ∠4, write the relation between ∠1 and ∠2, using an Euclid’s axiom.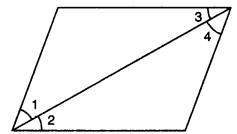 Ans:
Ans:
Here, ∠3 = ∠4, ∠1 = ∠3 and ∠2 = ∠4. Euclid’s first axiom says, the things which are equal to equal thing are equal to one another. So ∠1 = ∠2.,
Q7: In the given figure, AB = BC, BX = BY, show that AX = CY. Ans:
Ans:
Given that AB = BC and BX = BY
By using Euclid’s axiom 3, equals subtracted from equals, then the remainders are equal, we have
AB – BX = BC – BY
AX = CY
Q8: In the given figure, AC = DC and CB = CE. Show that AB = DE. Write the Euclid’s axiom to support this.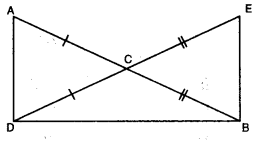 Ans:
Ans:
We have
AC = DC
CB = CE
By using Euclid’s axiom 2, if equals are added to equals, then wholes are equal.
⇒ AC + CB = DC + CE
⇒ AB = DE.
Q9: Define : (a) a square (b) perpendicular lines.
Ans:
(a) A square : A square is a rectangle having same length and breadth. Here, undefined terms are length, breadth and rectangle.
(b) Perpendicular lines : Two coplanar (in a plane) lines are perpendicular, if the angle between them at the point of intersection is one right angle. Here, the term one right angle is undefined.
Q10: If A, B and C are any three points on a line and B lies between A and C (see figure), then prove that AB + BC = AC. Ans: In the given figure, AC coincides with AB + BC. Also, Euclid’s axiom 4, states that things which coincide with one another are equal to one another. So, it is evident that:
Ans: In the given figure, AC coincides with AB + BC. Also, Euclid’s axiom 4, states that things which coincide with one another are equal to one another. So, it is evident that:
AB + BC = AC.
|
44 videos|412 docs|54 tests
|

|
Explore Courses for Class 9 exam
|

|

















