Short Review of Trigonometry | Quantitative Aptitude for Competitive Exams - SSC MTS / SSC GD PDF Download
Short Review of Trigonometry
First, let’s review the fundamentals.
Triangle Trig
Suppose that triangle ABC is right, and assume that ∠ C is the right angle. To find the sine, cosine, and tangent of ∠ A, just remember: SOHCAHTOA!

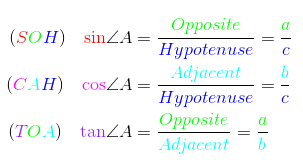
The tangent can also be defined in terms of sine and cosine — as can the three other trigonometric ratios. Let’s call θ = ∠ A.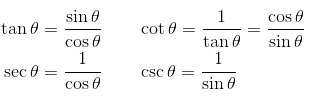
The Unit Circle
You should also be familiar with the Unit Circle. Each point (x, y) on the circle gives the value of cosine and sine of the corresponding angle.
For example, look for the angle 2π/3 (radians). Based on the unit circle diagram, you know:
- cos 120° = -1/2.
- sin 120° = √ 3 /2.
Trigonometric Functions
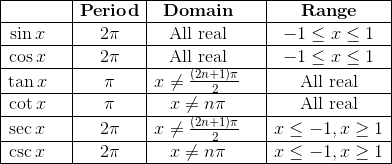
The six basic trig ratios can be extended to functions defined on all (or most) real numbers by interpreting arbitrary angles on the unit circle. The key is that each trig function becomes periodic, which means that values repeat in equal intervals.
It’s important to know the periods, domains, and ranges of each function.
The Pythagorean Identities
Perhaps the most famous and useful equation in all of mathematics is the Pythagorean Theorem. (For this and other essentials about triangles, check out: Triangle Properties to Know for the CAT).
When applied to the unit circle, we get a trio of useful trigonometric identities:
Sin2θ +cos2θ = 1, tan2θ+1 = sec2θ, 1+cot2θ = csc2θ
Other Useful Identities
Of course there are a myriad of other trigonometric identities, including sums or differences of angles, half and double angle formulas, products-to-sums, and sums-to-products, to name a few.
For a summary list, check out this table of trigonometric identities.
CAT Trigonometry Practice Problems
Now let’s test our knowledge and skills!
Q1. You are standing on the corner of a square whose side length is 25 feet. Standing on the opposite corner from you is a tall tree. The angle of elevation from your position to the top of the tree is exactly 60°. How tall is the tree?
A. 25√2
B. 25√3
C. 25√6
D. 50√3
Answer: 25√6
Explanation -
First find the distance of the diagonal d along the ground from corner to corner. Using Pythagorean theorem with sides 25 and 25, we get:
252 + 252 = d2
2 × 252 = d2
d = 25√ 2 .
Then to obtain the height h of the tree, use the tangent ratio with angle 60°.
tan 60° = x/(25√2)
√3 = x/(25√2)
x = 25√2 × √3 = 25√6
Q2.Tweedledee and Tweedledum are 100 m from each other. Between them there is a tower. Tweedledee notes that the top of the tower is at x°, while Tweedledum records that the top of the tower is at y°. Which expression below correctly computes the height of the tower?
A. 100 tan x° tan y° / (tan x° + tan y°)
B. 100 (tan x° + tan y°) / (tan x° – tan y°)
C. 100 (tan x° + tan y°) / (tan x° tan y°)
D. 100 tan x° tan y° / (tan x° – tan y°)
Answer: 100 tan x° tan y° / (tan x° + tan y°)
Explanation -
First let d represent the distance from Tweedledee to the tower. Then the distance from Tweedledum to the tower must be 100 – d. Next, let h be the height of the tower. So, there are two right triangles, one determined by Tweedledee and the other by Tweedledum, sharing the same height. Finally, use trigonometry to write two equations:
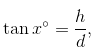
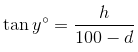
Next, solve the first equation for d:
d tan x° = h → d = h / tan x°
Now plug this result into the second equation and isolate h.
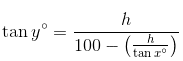
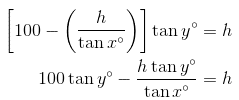
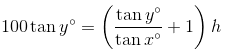
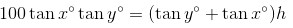
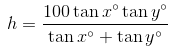
Q3. What is the maximum value of 8 sin θ + 6 cos θ?
A. 9.5
B. 10
C. 10.3
D. 10.8
Answer: 10
Explanation -
Here, the clue is that 6 and 8 form part of a Pythagorean Triple: 6-8-10.
Let f = 8 sin θ + 6 cos θ, and divide both sides by the constant 10 to get:
f/10 = (8/10) sin θ + (6/10) cos θ
Because 10 is constant, it’s equivalent to find a maximum value for f/10.
Next, we can assume that θ is a first-quadrant angle (otherwise, either its sine value or cosine value would be negative). So construct a right triangle with angle θ.
Now the trick is to compare this triangle to the one whose sides are in ratio 6 : 8 : 10. In fact, in a triangle whose adjacent side is 8 and opposite side is 6, then the hypotenuse would be 10. So, calling the angle of this new triangle φ, we can identify:
Then, sin φ = 6/10 and cos φ = 8/10.
Fortunately, these ratios already show up in our equation. (That’s why I picked the 6-8-10 triangle to compare to!) So we may substitute for the trig ratios:
f/10 = cos φ sin θ + sin φ cos θ
Next, using the sum of angles formula for sine, we could write:
f/10 = sin(φ + θ)
What is the maximum value of this function? Remember, the range of sin x is from -1 up to 1. So the maximum occurs when sin(φ + θ) = 1. This will happen as long as φ + θ = 90°. In other words, the unknown angle θ must be complementary to the angle of a 6-8-10 triangle. That makes our unknown triangle into a 6-8-10 triangle as well!
But the bottom line is that we can find such an angle, and so the maximum sine value (1) will be obtained. Finally, use f/10 = 1 (maximum) to find that f = 10.
Q4. Suppose the angle of elevation of the top of a flag pole changes from x° to 45° as you walk 15 m toward it. Assuming that x < 45, find the height of the flag pole in terms of x.
A. 30(1 + tan x°) / tan x°
B. 45 tan x° / (1 + tan x°)
C. 15 tan x° / (1 + tan x°)
D. 15 tan x° / (1 – tan x°)
Answer: 15 tan x° / (1 – tan x°)
Explanation -
Let h be the height of the flag pole. When you reach the point at which the angle of elevation is exactly 45°, then you are at the base of an isosceles right triangle with height h. Therefore, at that point, you are h meters from the base of the flag pole. Thus your original position was 15 + h meters from the pole.
This information allows us to set up a trigonometric equation: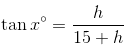
(15+h) tanx° = h
15tanx° + h tanx° = h
15tanx° + (1 - tanx°)h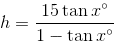
|
203 videos|110 docs|114 tests
|
FAQs on Short Review of Trigonometry - Quantitative Aptitude for Competitive Exams - SSC MTS / SSC GD
| 1. What is trigonometry? |  |
| 2. How is trigonometry useful in real life? |  |
| 3. What are the primary trigonometric functions? |  |
| 4. How do you solve trigonometric equations? |  |
| 5. What is the Pythagorean theorem and its connection to trigonometry? |  |






















