Simple harmonic oscillations | Basic Physics for IIT JAM PDF Download
Consider a mass m held in an equilibrium position by springs, as shown in Figure(A). The mass may be perturbed by displacing it to the right or left. If x is the displacement of the mass from equilibrium Figure(B), the springs exert a force F proportional to x, such that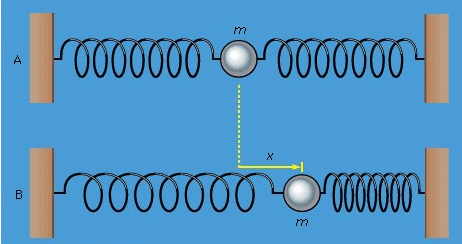
Figure 2(A) A mass m held in equilibrium by springs.(B) A mass m displaced a distance x.
f = -kx (10)
where k is a constant that depends on the stiffness of the springs. Equation is called Hooke’s law, and the force is called the spring force. If x is positive (displacement to the right), the resulting force is negative (to the left), and vice versa. In other words, the spring force always acts so as to restore mass back toward its equilibrium position. Moreover, the force will produce an acceleration along the x direction given by a = d2x/dt2. Thus, Newton’s second law, F = ma, is applied to this case by substituting −kx for F and d2x/dt2 for a, giving −kx = m(d2x/dt2). Transposing and dividing by m yields the equation
f = -kx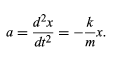 (11)
(11)
Equation (11) gives the derivative—in this case the second derivative—of a quantity x in terms of the quantity itself. Such an equation is called a differential equation, meaning an equation containing derivatives. Much of the ordinary, day-to-day work of theoretical physics consists of solving differential equations. The question is, given equation, how does x depend on time?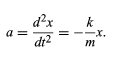 (11)
(11)
The answer is suggested by experience. If the mass is displaced and released, it will oscillate back and forth about its equilibrium position. That is, x should be an oscillating function of t, such as a sine wave or a cosine wave. For example, x might obey a behaviour such as
x = A cos ωt (12)
Equation (12) describes the behaviour sketched graphically in Figure 3. The mass is initially displaced a distance x = A and released at time t = 0. As time goes on, the mass oscillates from A to −A and back to A again in the time it takes ωt to advance by 2π. This time is called T, the period of oscillation, so that ωT = 2π, or T = 2π/ω. The reciprocal of the period, or the frequency f, in oscillations per second, is given by f = 1/T = ω/2π. The quantity ω is called the angular frequency and is expressed in radians per second.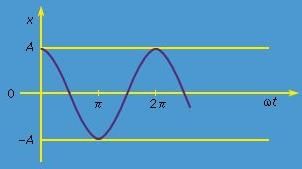
Figure: The function x = A cos ωt. (12)
The choice of equation (12) as a possible kind of behaviour satisfying the differential equation (11) can be tested by substituting it into equation (11). The first derivative of x with respect to t is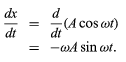 (13)
(13)
Differentiating a second time gives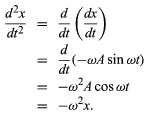 (14)
(14)
Equation (14) is the same as equation (11) if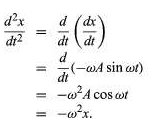 (14)
(14)
ω2 = k/m (15)
Thus, subject to this condition, equation (12) is a correct solution to the differential equation. There are other possible correct guesses (e.g., x = A sin ωt) that differ from this one only in whether the mass is at rest or in motion at the instant t = 0.
The mass, as has been shown, oscillates from A to −A and back again. The speed, given by dx/dt, equation (13), is zero at A and −A, but has its maximum magnitude, equal to ωA, when x is equal to zero. Physically, after the mass is displaced from equilibrium a distance A to the right, the restoring force F pushes the mass back toward its equilibrium position, causing it to accelerate to the left. When it reaches equilibrium, there is no force acting on it at that instant, but it is moving at speed ωA, and its inertia takes it past the equilibrium position. Before it is stopped it reaches position −A, and by this time there is a force acting on it again, pushing it back toward equilibrium.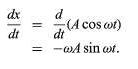 (13)
(13)
The whole process, known as simple harmonic motion, repeats itself endlessly with a frequency given by equation (15). Equation (15) means that the stiffer the springs (i.e., the larger k), the higher the frequency (the faster the oscillations). Making the mass greater has exactly the opposite effect, slowing things down.
ω2 = k/m (15)
One of the most important features of harmonic motion is the fact that the frequency of the motion, ω (or f), depends only on the mass and the stiffness of the spring. It does not depend on the amplitude A of the motion. If the amplitude is increased, the mass moves faster, but the time required for a complete round trip remains the same. This fact has profound consequences, governing the nature of music and the principle of accurate timekeeping.
The potential energy of a harmonic oscillator, equal to the work an outside agent must do to push the mass from zero to x, is U = 1/2kx2. Thus, the total initial energy in the situation described above is 1/2kA2; and since the kinetic energy is always 1/2mv2, when the mass is at any point x in the oscillation,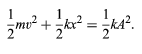 (16)
(16)
Equation (16) plays exactly the role for harmonic oscillators that equation (8) does for falling bodies.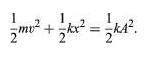 (16)
(16)
It is quite generally true that harmonic oscillations result from disturbing any body or structure from a state of stable mechanical equilibrium. To understand this point, a brief discussion of stability is useful.
Consider a bowl with a marble resting inside, then consider a second, inverted bowl with a marble balanced on top. In both cases, the net force on the marble is zero. The marbles are thus in mechanical equilibrium. However, a small disturbance in the position of the marble balanced on top of the inverted bowl will cause it to roll away and not return. In such a case, the equilibrium is said to be unstable. Conversely, if the marble inside the first bowl is disturbed, gravity acts to push it back toward the bottom of the bowl. The marble inside the bowl (like the mass held by springs in Figure 2A) is an example of a body in stable equilibrium. If it is disturbed slightly, it executes harmonic oscillations around the bottom of the bowl rather than rolling away.
This argument may be generalized by a simple mathematical argument. Consider a body or structure in mechanical equilibrium, which, when disturbed by a small amount x, finds a force acting on it that is a function of x, F(x). For small x, such a function may be written generally as a power series in x; i.e.,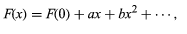 (17)
(17)
where F(0) is the value of F(x) when x = (0), and a and b are constants, independent of x, determined by the nature of the system. The statement that the body is in mechanical equilibrium means that F(0) = 0, so that no force is acting on the body when it is undisturbed. Since x is small, x2 is much smaller; thus, the term bx2 and all higher powers may be disregarded. This leaves F(x) = ax. Now, if a is positive, a disturbance produces a force in the same direction as the disturbance. This was the case when the marble was balanced on top of the inverted bowl. It describes unstable equilibrium. For the system to be stable, a must be negative. Thus, if a = −k, where k is some positive constant, equation (17) becomes F(x) = −kx, which is simply Hooke’s law, equation (10). As has been described above, any system obeying Hooke’s law is a harmonic oscillator.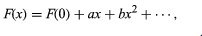 (17)
(17)
The generality of this argument accounts for the fact that harmonic oscillators are abundantly observed in common experience. For example, any rigid structure will oscillate at many different harmonic frequencies corresponding to different possible distortions of its equilibrium shape. In addition, music may be produced either by disturbing the equilibrium of a stretched wire or fibre (as in the piano and violin), a stretched membrane (e.g., drums), or a rigid bar (the triangle and the xylophone) or by disturbing the density of an enclosed column of air (as in the trumpet and organ). While a fluid such as air is not rigid, its density is an example of a stable system that obeys Hooke’s law and may therefore be set into harmonic oscillations.
All music would be quite different from what it is were it not for the general property of harmonic oscillators that the frequency is independent of the amplitude. Thus, instruments yield the same note (frequency) regardless of how loudly they are played (amplitude), and, equally important, the same note persists as the vibrations die away. This same property of harmonic oscillators is the underlying principle of all accurate timekeeping.
The first precise timekeeping mechanism, whose principles of motion were discovered by Galileo, was the simple pendulum (see below). The accuracy of modern timekeeping has been improved dramatically by the introduction of tiny quartz crystals, whose harmonic oscillations generate electrical signals that may be incorporated into miniaturized circuits in clocks and wristwatches. All harmonic oscillators are natural timekeeping devices because they oscillate at intrinsic natural frequencies independent of amplitude. A given number of complete cycles always corresponds to the same elapsed time. Quartz crystal oscillators make more accurate clocks than pendulums do principally because they oscillate many more times per second.
|
217 videos|156 docs|94 tests
|
FAQs on Simple harmonic oscillations - Basic Physics for IIT JAM
| 1. What is simple harmonic motion? |  |
| 2. How is the period of a simple harmonic oscillator related to its frequency? |  |
| 3. What is the amplitude of a simple harmonic oscillator? |  |
| 4. How does the mass affect the period of a simple harmonic oscillator? |  |
| 5. What is the relationship between the potential energy and kinetic energy in a simple harmonic oscillator? |  |
















