Class 10 Exam > Class 10 Notes > Mathematics for GCSE/IGCSE > Simultaneous Equations
Simultaneous Equations | Mathematics for GCSE/IGCSE - Class 10 PDF Download
Linear Simultaneous Equations
What are linear simultaneous equations?
- Linear simultaneous equations involve two unknowns, typically represented as x and y.
- To solve for both variables, you need two equations that can be solved simultaneously.
- For instance, consider the equations 3x - 2y = 11 and 2x - y = 5.
- By solving these equations together, you can determine that x = 3 and y = 1.
- To solve for both variables, you need two equations that can be solved simultaneously.
- If they just have x and y in them (no x2 or y2 or xy etc) then they are linear simultaneous equations
How do I solve linear simultaneous equations by elimination?
- "Elimination" involves eliminating one of the variables, x or y, from the equations. For instance:
- To eliminate the x's from 3x - 2y = 11 and 2x - y = 5, follow these steps:
- Multiply every term in the first equation by 2: 6x - 4y = 22
- Multiply every term in the second equation by 3: 6x - 3y = 15
- Subtract the second result from the first to eliminate the 6x's, resulting in 4y - (-3y) = 22 - 15, simplifying to 7y = 7
- Solve for y (y = 1) and substitute y = 1 back into either original equation to find x (x = 3)
- To eliminate the y's, follow a similar process:
- Multiply every term in the second equation by 2: 4x - 2y = 10
- Add this result to the first equation to eliminate the 2y's, as 2y - 2y = 0
- Continue solving for x and y as described above
- Check your final solutions satisfy both equations.
How do I solve linear simultaneous equations by substitution?
- "Substitution" means substituting one equation into the other
- Solve 3x + 2y = 11 and 2x - y = 5 by substitution
- Rearrange one of the equation into y = ... (or x = ...)
- For example, the second equation becomes y = 2x - 5
- Substitute this into the first equation (replace all y's with 2x - 5 in brackets)
- 3x + 2(2x - 5) = 11
- Solve this equation to find x (x = 3), then substitute x = 3 into y = 2x - 5 to find y (y = 1)
- Rearrange one of the equation into y = ... (or x = ...)
- Check your final solutions satisfy both equations
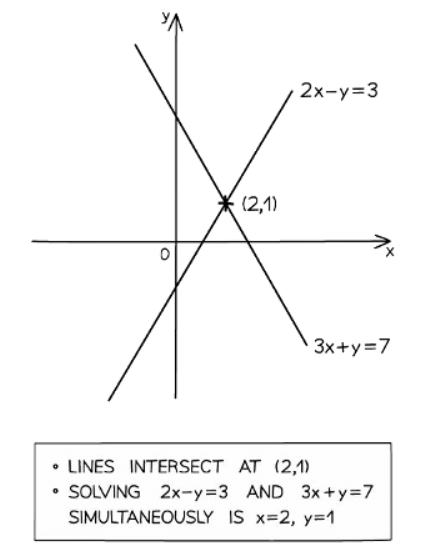
How do you use graphs to solve linear simultaneous equations?
- Plot both equations on the same set of axes. You can use a table of values or rearrange them into y = mx + c form if needed.
- Find where the lines intersect. The solutions to the simultaneous equations are the coordinates of this point of intersection.
- For example, consider solving 2x - y = 3 and 3x - y = 4 simultaneously. After plotting and finding the intersection point (2, 1), the solution is x = 2 and y = 1.
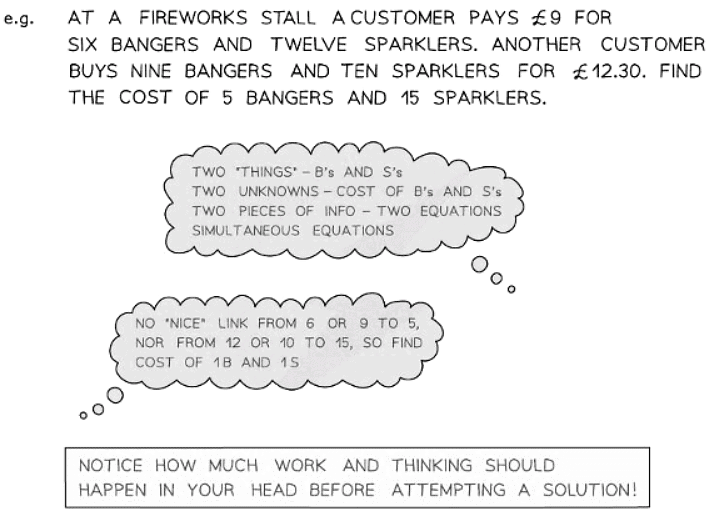
How do I solve linear simultaneous equations from worded contexts?


 Quadratic Simultaneous Equations
Quadratic Simultaneous Equations
What are quadratic simultaneous equations?
- When there are two unknowns (say x and y) in a problem, we need two equations to be able to find them both: these are called simultaneous equations
- If there is an x2 or y2 or xy in one of the equations, then they are quadratic (or non-linear) simultaneous equations
How do I solve quadratic simultaneous equations?
Steps to Solve Quadratic Simultaneous Equations:
- Using the Substitution Method:
- Substitute the linear equation, either y = ... or x = ..., into the quadratic equation, avoiding the reverse substitution.
- Key Steps:
- Solve x2 - y2 = 25 and y - 2x = 5.
- Rearrange the linear equation to y = 2x - 5.
- Replace all y's with (2x - 5) in brackets in the quadratic equation: x2 - (2x - 5)2 = 25.
- Expand and solve the quadratic equation to find x = 0 and x = -4.
- Substitute each x value into y = 2x - 5 to determine the corresponding y value.
- Present solutions clearly: x = 0, y = 5 or x = -4, y = -3.
- Check your final solutions satisfy both equations.
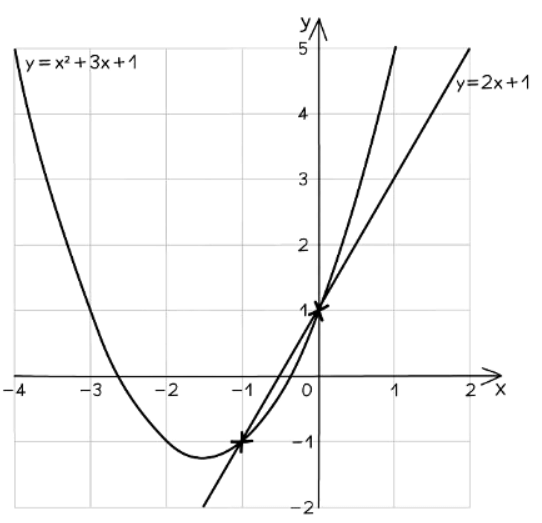
How do you use graphs to solve quadratic simultaneous equations?
- When plotting two equations on the same set of axes, a table of values can be utilized. For linear equations, it may be beneficial to rearrange them into the form y = mx + c.
- Locate the points where the lines intersect. These points represent the solutions to the simultaneous equations, providing the coordinates of the intersection.
- For instance, consider solving the equations y = x^2 - 3x - 1 and y = 2x - 1 simultaneously. By plotting both equations and finding their points of intersection at (-1, -1) and (0, 1), the solutions emerge as x = -1, y = -1 or x = 0, y = 1.
The document Simultaneous Equations | Mathematics for GCSE/IGCSE - Class 10 is a part of the Class 10 Course Mathematics for GCSE/IGCSE.
All you need of Class 10 at this link: Class 10
|
38 videos|413 docs|19 tests
|
Related Searches
















