Class 10 Exam > Class 10 Notes > Mathematics for GCSE/IGCSE > Sine & Cosine Rules
Sine & Cosine Rules | Mathematics for GCSE/IGCSE - Class 10 PDF Download
Sine Rule
What is the sine rule?
- The sine rule helps us determine missing side lengths or angles in triangles that are not right-angled.
- It is applicable to any triangle with angles A, B, and C.
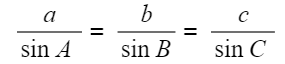
- Where,
- a is the side opposite angle A
- b is the side opposite angle B
- c is the side opposite angle C
- When one of the angles in the triangle is 90 degrees, the sine rule simplifies to SOH (Sine = Opposite/Hypotenuse) from SOHCAHTOA.
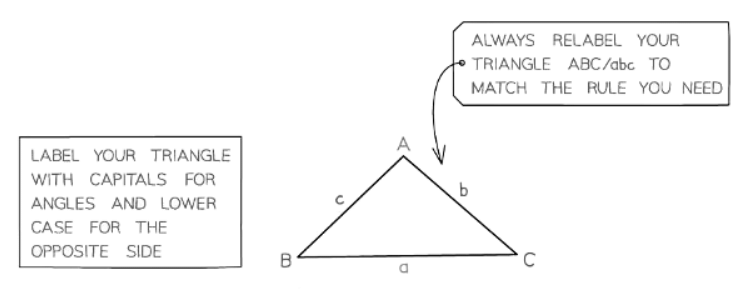
How can we use the sine rule to find missing side lengths or angles?
- The sine rule is applicable when dealing with any opposite pairs of sides and angles in a triangle.
- Begin by labeling the triangle with the corresponding angles and sides. Note that the sides denoted with lowercase letters are opposite the angles indicated by the corresponding uppercase letters.
- Employ the sine rule formula to determine the length of a side.
- To ascertain a missing angle, rearrange the formula into the form:
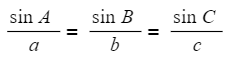
- Substitute the known values into the formula and solve accordingly.
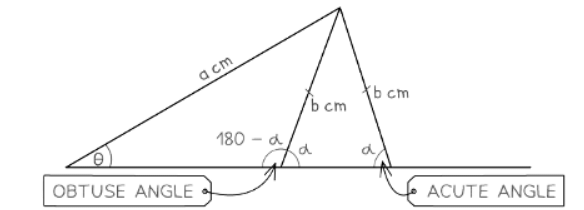
What is the ambiguous case of the sine rule?
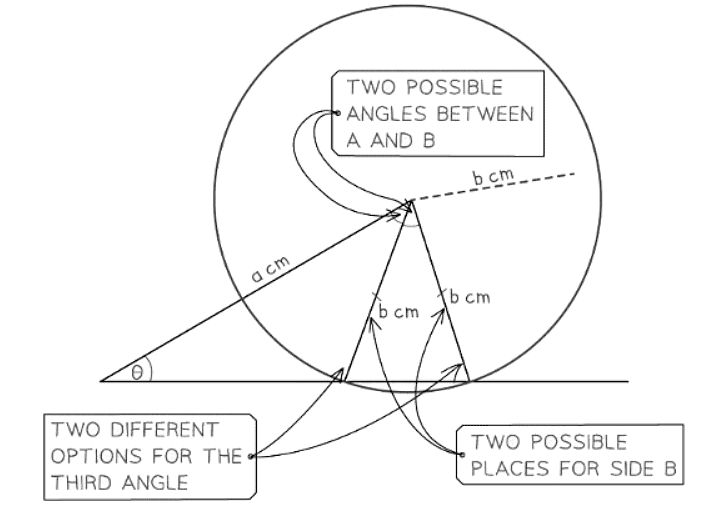
- When using the sine rule in a triangle with two sides and an angle (not the angle between them) given, there might be multiple possible triangles that can be formed.
- The side opposite the given angle could be in two potential positions, leading to two possible values for each of the missing angles and two possible lengths for the missing side.
- The two angles found opposite the given side (not the ambiguous side) will add up to 180°.
- Usually, the question specifies whether the angle you are searching for is acute or obtuse.
- The sine rule typically provides the acute angle option, but you can subtract from 180° to determine the obtuse angle.
- Sometimes, the obtuse angle may not be valid as it could cause the sum of the triangle's three interior angles to exceed 180°.
Cosine Rule
What is the cosine rule?
- The cosine rule allows us to find missing side lengths or angles in non-right-angled triangles
- It states that for any triangle:
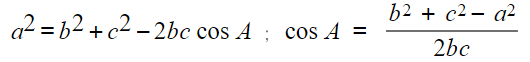
- Where,
- a is the side opposite angle A
- b and c are the other two sides
- Both of these formulae are rearrangements of the same thing
- The first version is used to find a missing side
- The second version is a rearrangement of this and can be used to find a missing angle
- Cos 90° = 0 so if A = 90° this becomes Pythagoras’ Theorem
How can we use the cosine rule to find missing side lengths or angles?
- The cosine rule proves useful in scenarios where you possess either two sides and the angle between them or all three sides.
- Begin by labeling your triangle with the corresponding angles and sides. Note that the sides denoted with lowercase letters are opposite the angles indicated by the equivalent uppercase letters.
- Utilize the formula a2 = b2 + c2 − 2bc ⋅ cosA to determine an unknown side, where A is the angle between sides b and c.
- To find an unknown angle, use the formula
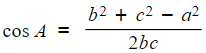
- Substitute the known values into the respective formula and solve accordingly.
Question for Sine & Cosine RulesTry yourself: What is the sine rule used for?View Solution
The document Sine & Cosine Rules | Mathematics for GCSE/IGCSE - Class 10 is a part of the Class 10 Course Mathematics for GCSE/IGCSE.
All you need of Class 10 at this link: Class 10
|
66 videos|674 docs|19 tests
|
FAQs on Sine & Cosine Rules - Mathematics for GCSE/IGCSE - Class 10
| 1. What is the Sine Rule? |  |
Ans. The Sine Rule, also known as the Law of Sines, is a trigonometric formula used to find the lengths and angles of a triangle. It states that the ratio of the length of a side of a triangle to the sine of the angle opposite that side is constant for all three sides of the triangle.
| 2. What is the Cosine Rule? |  |
Ans. The Cosine Rule, also known as the Law of Cosines, is a trigonometric formula used to find the lengths of the sides and angles of a triangle. It states that the square of a side of a triangle is equal to the sum of the squares of the other two sides minus two times the product of those sides and the cosine of the angle between them.
| 3. When do you use the Sine Rule in trigonometry? |  |
Ans. The Sine Rule is used in trigonometry when you have a triangle with an angle and its opposite side known, or when you have two angles and a side known. It is particularly useful for solving oblique triangles, where not all angles are right angles.
| 4. When do you use the Cosine Rule in trigonometry? |  |
Ans. The Cosine Rule is used in trigonometry when you have a triangle with all three sides known or when you have two sides and the included angle known. It is especially helpful in solving triangles where all three sides are known, but not all angles.
| 5. How do the Sine Rule and Cosine Rule differ in their applications in trigonometry? |  |
Ans. The Sine Rule is primarily used to find the missing sides or angles of a triangle when you know the lengths of some sides and the angles opposite them. In contrast, the Cosine Rule is used to find the missing sides or angles of a triangle when you know the lengths of all three sides or two sides and the included angle.
Related Searches
















