Lakhmir Singh & Manjit Kaur: Work and Energy, Solutions- 1 | Science Class 9 PDF Download
Page 145
Solution 1
Mass = m
Height above the ground = h
Work done = Potential energy acquired by the body = m x g x h
where g is acceleration due to gravity
Solution 2
SI unit of work is Joule (J).
Solution 3
Work is a scalar quantity.
Work, as a physical quantity, requires only magnitude to be represented. Hence, it is scalar quantity.
Solution 4
When a force of 1 newton moves a body through a distance of 1 metre in its own direction, then the work done is known as 1 joule.
Solution 5
The condition for a force to do work on a body is that it should produce motion in the body.
Solution 6
Energy is a scalar quantity. It has only magnitude but no direction.
Solution 7
a)Unit of work is joule.
b) Unit of energy is joule.
Solution 8
The work done against gravity is zero when a body is moved horizontally along a frictionless surface because force of gravity acts perpendicular to the direction of motion.
Solution 9
Kinetic energy will become four times when the speed is doubled because kinetic
energy is directly proportional to square of speed of the body
K.E ∝ V2
Solution 10
Mass = m
Velocity = v

Solution 11
Kinetic
energy will become one-fourth when the speed is halved because kinetic energy
is directly proportional to square of speed of the body
K.E ∝ V2
Solution 12
The kinetic energy of a body depends on
a) Mass of the body, m
b) Square of the velocity of the body, v2
Solution 13
Doubling the velocity would have a greater effect on kinetic energy.
Solution 14
Mass = 50 kg
Kinetic energy = 625 J
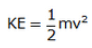

Solution 15
a) Both kinetic and potential energy
b) Both kinetic and potential energy
c) Only kinetic energy
d) Only potential energy
e) Only potential energy
Note: In all the above cases we take ground as reference level where potential energy is zero.
Solution 16
Let masses of body A and B be m
Height of body A = h
Height of body B = 2h
Potential energy for body A, PEA = m x g x h
Potential energy for body B, PEB = m x g x 2h

Solution 17
Mass = 1 kg
Velocity = 2 m/s
K.E. 
Solution 18
Potential energy is a scalar quantity as it has magnitude only and it does not require any specification of direction.
Solution 19
Mass = 100 kg
Height = 5 m
g = 9.8 m/s2
P.E. = m x g x h = 100 x 5 x 9.8 = 4900 J
Work done is equal to PE acquired by the body.
Solution 20
False.
PE = m x g x h
= 1 x 9.8 x 1 = 9.8 J
Solution 21
The potential energy is doubled when the height is doubled since potential energy is directly proportional to height, h to which body is raised.
PE ∝ h
Solution 22
a) Potential energy
b) Kinetic energy
c) Potential energy
d) Potential energy
e) Potential energy
Solution 23
a) Force ; distance
b) Zero
c) newton; metre; force
d) Energy; kinetic energy
e) mechanical
Solution 24
The work done by a force on a body depends on two factors
a) magnitude of force
b) distance through which the body moves
Work done is directly proportional to the force applied and the distance through which the body moves.
W = F x s
where W is work done, F is force applied and s is distance through which the body moves.
Solution 25
Yes, it is possible that a force is acting on a body but still work done is zero. For example, in the case of a man pushing a wall, the work done is zero despite of non-zero force, sin ce there is no displacement of the wall.
Page No - 146
Solution 26
a) Work done by force applied by the boy is positive because this force is in the direction of motion of the body.
b) Work done by the gravitational force is negative because this force is against the direction of motion of the body.
Solution 27
W = F cos θ x s
where w is work done
F is force applied
θ is angle between the direction of force and the direction of motion of the body
s is the distance moved by the body
Solution 28
Kinetic energy is directly proportional to the mass of the body, m
KE ∝ m
Kinetic energy is directly proportional to the square of speed of the body, v
KE ∝ v2
Solution 29
(a) Positive work: Work done by the force applied by a person on a ball that is thrown upwards.
(b) Negative work: Work done by gravitational force of earth on a ball thrown upwards.
(c) Zero work: Work done by gravitational force of earth on a box that is sliding horizontally on the ground.
Solution 30
Mass 200 gm = 0.2 kg
Height = 5 m
intial velocity u = 0
Acceleration due to gravity = g = 9.8 m/s2
final velocity , v
using third equation of motion
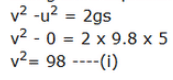
Kinetic energy = 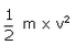
Put the value of v2 from eqn. 1
Kinetic energy = 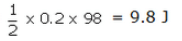
Solution 31
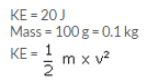

Solution 32
Let mass of two object be m
v1 = 2m/s
v2= 6 m/s
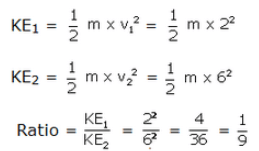
Solution 33
Mass of body = 2 kg
Initial velocity u = 0
Time taken = 2 s
Acceleration due to gravity, g = 10 m/s2
Final velocity v
Using first equation of motion
v = u + gt = 0 + 10 x 2 = 20 m/s
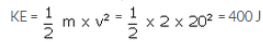
Solution 34
Mass of scooter + scooterist = 150 kg
Initial velocity u = 10 m/s
Final velocity v = 5 m/s
Retardation = a
Distance covered= s
Using third equation of motion
v2 – u2 = 2as
52 – 102 = 2as
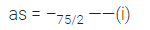
Work done W = F x s
But F = m x a
So, W= m x a x s
Put the value of ‘as’ from eq(i)
W = 150 x (-75/2) = -5625 J
Neagtive sign implies that force of brakes acts opposite to the direction of motion.
Solution 35
Mass of rock = 10 kg
Height of ladder, h = 5 m
Initial velocity of rock, u = 0
Final velocity v
g = 10 m/s2
using third equation of motion
v2 – u2 = 2gh
v2 – 02 = 2 x 10 x 5
v = 10 m/s
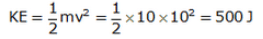
Solution 36
Mass of car = 1000 kg
Initial velocity u = 20 m/s
Final velocity v = 10 m/s
Retardation = a
Distance covered = s
Using third equation of motion
v2 -u2 = 2as
102– 202 = 2as
as = -150 ——(i)
Work done W = F x s
But F = m x a
So, W= m x a x s
Put the value of ‘as’ from equation (i)
W = 1000 x -150 = -150000 = -150 kJ Neagtive sign implies that force of brakes acts opposite to the direction of motion.
Solution 37
Height , h= 10 m
Acceleration due to gravity, g = 10 m/s2
i) Work done, W = m x g x h = 100 x 10 x 10 = 10000 = 10 kJ
ii) Potential energy of the body = work done = 10 kJ
Solution 38
Height, h = 100 m
Acceleration due to gravity, g = 9.8m/s2
Work done by the boy, W = m x g x h = 50 x 9.8 x 100 = 49000 J = 49 kJ
Potential energy gained by the boy = work done by the boy = 49 kJ
Solution 39
Work done by a force applied on a body is
i) positive when the force acts in the direction of motion of the body.
ii) negative when the force acts in the direction opposite to the direction of motion of the body.
iii) zero when the force acts at right angle to the direction of motion of the body.
Solution 40
Mass of the box, m = 150 kg
PE = 7350 J
Acceleration due to gravity, g = 9.8m/s2
PE = m x g x h
7350 = 150 x 9.8 x h
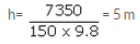
Solution 41
Mass of the body, m = 2 kg
Initial velocity, u = 20 m/s
Acceleration due to gravity, g = 10 m/s2
Height reached = h
Time, t = 2 s
Using second equation of motion
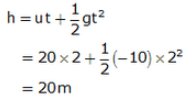
PE after 2 s = m x g x h = 2 x 10 x 20 = 400 J
Solution 42
Force, F = 1 N
Distance, s = 1 m
Work done W = F x s = 1 x 1 = 1 J
Solution 43
Force, F = 2.5 x 1010 N
Velocity, v = 5 m/s
Time, t = 2 minutes = 120 s
Distance, s = v x t = 5 x 120 = 600 m
Work done, W = F x s = 2.5 x 1010 x 600 = 15 x 1012 J
Solution 44
A stretched rubber band is an example of a body possessing energy while it is not in motion. The rubber band contains potential energy due to the change in its shape or configuration.
Solution 45
a)Gravitational potential energy of a body depends on:
i)mass of the body, m
ii)height to which the body is lifted, h
iii)acceleration due to gravity, g
b)
i.A moving cricket ball has kinetic energy
ii.A stretched rubber band has potential energy
Solution 46
Two examples where a body possesses both kinetic energy as well as potential energy are
i)a man climbing up a hill
ii)a flying aeroplane
Solution 47
Mass of man, m
Height of tree, h = 5 m
Work done, W = 2500 J
Acceleration due to gravity, g = 10 m/s2
W = m x g x h
2500 = m x 10 x 5
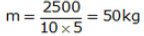
Solution 48
Work done, W =24.2 J
Distance, s = 20 cm = 0.2 m
Force, F
W = F x s
24.2 = F x 0.2
F = 24.2/0.2 = 121 N
Solution 49
Mass of boy, m = 40 kg
Height, h = 1.5 m
Acceleration due to gravity, g = 10 m/s2
i)At highest point, velocity, v = 0
Therefore KE = 0
ii)PE = m x g x h = 40 x 10 x 1.5 = 600 J
Solution 50
a) Potential energy
b) Both potential and kinetic energy
|
88 videos|369 docs|67 tests
|
FAQs on Lakhmir Singh & Manjit Kaur: Work and Energy, Solutions- 1 - Science Class 9
| 1. What is work and energy? |  |
| 2. How is work calculated? |  |
| 3. What is the unit of work and energy? |  |
| 4. What are the different types of energy? |  |
| 5. How is energy converted from one form to another? |  |

|
Explore Courses for Class 9 exam
|

|

















