Solved Examples: Arithmetic Progressions | Quantitative Aptitude for SSC CGL PDF Download
Definition of Arithmetic Progression (AP)
An arithmetic progression can be defined as a sequence in which the difference between each consecutive pair of numbers or terms remains constant.
Notations in Arithmetic Progression (AP)
- Initial term (a): In an arithmetic progression, the first number in the series is called the initial term.
- Common difference (d): The ‘d’ denotes the variance between all the consecutive terms of the progression.
- Nth term (an): The an defines the terms of the progression or sequence whereas ‘n denotes the position of the given number or alphabet which can be obtained by an = a + (n − 1)d.
- Sum of AP (Sn): The sum of an AP can be obtained by Sn = n/2 [2a + (n − 1) d]
If ‘n’ is equal to one then it denotes the initial term of arithmetic progression. This is known as the precise method for an Arithmetic progression.
General form of AP:
The general form of an AP is : a, a + d, a + 2d, a + 3d, …….
Finite or Infinite Arithmetic Progressions
- Finite Arithmetic Progression: When there are limited number of terms in the sequence then it is known as Finite Arithmetic Progression.
For example: 10, 20, 30, 40, 50 - Infinite Arithmetic Progression: When there are unlimited number of terms in the sequence then it is known as Infinite Arithmetic Progression.
For example: 3, 5, 7, 9, 11, 13, ..…….
Note: The nature of a sequence is dictated by a common difference.
- When the difference (d) is positive, the terms of the sequence will ascend towards positive infinity.
- If the difference is negative, the terms of the sequence will ascend towards negative infinity.
Arithmetic Progression Questions and Answers
Q1: Find the 1st term of the AP whose 6th and 10th terms are respectively 36 and 56.
(a) 8
(b) 9
(c) 10
(d) 11
Ans: (d)
As we know about the nth term of AP is [a + (n-1)d]
So, 6th term = a + 5d
and 10th term = a + 9d
Given a + 5d = 36 ………(1)
a + 9d = 56……….(2)
Subtract (1) form (2)
4d = 20
d = 5
put value of d in (1)
a + 5×5 = 36
a =11
Hence, 1st term of the AP is 11.
Q2: How many natural numbers between 300 to 500 are multiples of 40?
(a) 3
(b) 4
(c) 5
(d) 6
Ans: (c)
The series have multiple starting from 320, 360, ……..480
It becomes an AP having common difference 40.
Total number of natural numbers = 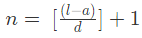
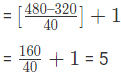
Q3: In the given arithmetic progression, ’44’ would be a term in it.
17, 20, 23, 26, 29, 32………62.
(a) True
(b) False
(c) can not say
(d) None
Ans: (a)
nth term = a + (n-1)d
44 = 17 + (n-1)3,
n = 30/3 = 10
n = 10
Clearly 10 is an integer. So 44 is a term in this series.
Q4: Anupam joins a company Pidilite industries in January 2018 and he get his first pay of Rs 2000. After that he got an increment every month of Rs 1500. Calculate his total pay after the end of 5 years of his job.
(a) 80000
(b) 85000
(c) 90500
(d) 92000
Ans: (c)
It is an AP 2000, 3500, 5000, ……..so on.
As we know in total there 60 months in 5 years.
We need to calculate the 60th term of the series.
Common difference d = 1500
a60 = a + (n-1)d
a60 = 2000 + 59 x 1500
a60 = 2000 + 88500 = 90500
After completion of 5 years of service his salary will be Rs 90500.
Q5: 8th term of the series 2√4+√4+0+..... will be
(a) −5√4
(b) 4√4
(c) 10√2
(d) -10√2
Ans: (a)
Clearly the given series is in Arithmetic progression
2√4+√4+0+..... is an A.P.
Now
a=2√4, d=−√4.
Hence 8th term of the series
=2√4+(8−1)(−√4)=−5√4.
Q6: A figure 24 is distributed into three parts which are in Arithmetic Progression and total of their squares is 208.
(a) 8.5
(b) 9
(c) 10.9
(d) 11
Ans: (c)
Let the three consecutive parts of AP are (a-d), a, (a+d).
Given that
(a-d) + a + (a+d) = 24
3a = 24
a = 8
Again, (a-d)2 + a2 + (a+d)2 = 208
a2 + d2 – 2ad + a2 + a2 + d2 + 2ad = 208
3a2 + 2d2 = 208
put value of a
3(8)2 + 2d2 = 208
2d2 = 208 – 192
d2 = 8
d = ∓2.9
Hence, the largest part is (a+d) = 8+2.9 = 10.9
Q7: In the given arithmetic progression, ’33’ would be a term in it. 7, 10, 13, 16, 19, 22………52.
(a) True
(b) False
(c) can not say
(d) None
Ans: (b)
nth term = a + (n-1)d, 33 = 7 + (n-1)3,
n = 29/3
n = 9.666
Clearly 9.66 is not an integer. So 33 is not a term in this series.
Q8: An elastic toy bounces (3443 )th of its height after touching to the base from which it has fall over. Calculate the full distance that it travels before coming to rest, if it is mildly fallen from a top of 360 metres.
(a) 5400
(b) 5300
(c) 2520
(d) 4800
Ans: (c)
It becomes an infinite sum of series.
So, use 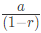 to calculate the distance
to calculate the distance
Ball rebounds to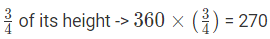
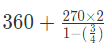
= 360 + 2160
= 2520
Hence, the full distance of elastic toy = 2520
Q9: The sequence 9√5, 8√5, 7√5, …….. is
(a) Arithmetic progression
(b) Geometric progression
(c) Harmonic progression
(d) None of these
Ans: (a)
Difference is: d = 8√5-9√5 = 7√5-8√5 = -√5
Therefore given arrangement is in Arithmetic progression.
Q10: If the 8th term of an Arithmetic Progression be zero, then the ratio of its 28th and 18th term will be?
(a) 1 : 2
(b) 2 : 2
(c) 2 : 1
(d) 3 : 1
Ans: (c)
Given that 8th term = 0
8th term = a+(8−1)d = a+7d
so a+7d = 0
Now ratio of 28th and 18th terms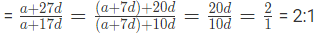
|
314 videos|170 docs|185 tests
|
|
314 videos|170 docs|185 tests
|

|
Explore Courses for SSC CGL exam
|

|
















