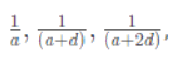Solved Examples: Harmonic Progressions | Quantitative Aptitude for SSC CGL PDF Download
Definition of HP
A Harmonic progression is a kind of sequence of real numbers made after procuring the reciprocal of the arithmetic progression.
General form of Harmonic Progression
- It can be categorized as a set of real numbers where each term within the sequence represents the harmonic mean of its two adjacent numbers.
- Additionally, when the reverse of the sequence adheres to the principles of an arithmetic progression, it is referred to as a harmonic progression.
- It basically means that if a, a + d, a + 2d, and so on is an A.P. then

Key Points
- The terms in a harmonic progression are invariably positive and non-zero. This requirement arises from the necessity to define reciprocals of the terms, as division by zero remains undefined.
- In contrast to arithmetic and geometric progressions, harmonic progressions lack a finite sum. The total of the terms in a harmonic progression diverges, indicating that it tends towards infinity as more terms are added.
Solved Examples
Example 1: Find maximum partial sum of harmonic progression, if second and third terms are 1/13 and 1/10 respectively.
(a) 1.23
(b) 1.63
(c) 1.25
(d) 1.09
Ans: (b)
The terms of the HP are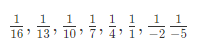
So the maximum partial sum is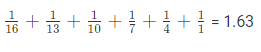
Example 2: For 2 numbers U, V, Harmonic Mean among them will be?
(a) (2v + 2u )/3v
(b) 2uv/(u + v)
(c) (u + v)/2uv
(d) 2v/(u + v)
Ans: (b)
Let w be the harmonic mean, 2⁄w = 1⁄u + 1⁄v,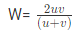
Example 3: If p, q, r are in h.p, then q is connected with p and r as :
(a) 2(1⁄q) = (1⁄p + 1⁄r)
(b) 2(1⁄r) = (1⁄q + 1⁄r)
(c) 2(1⁄p) = (1⁄p + 1⁄q)
(d) None of the mentioned
Ans: (d)
1⁄p, 1⁄q, 1⁄r will be in a.m. series and 1⁄q will be the A.M of p, r.
Example 4: Find the 11th term of the H.P.
1/4, 1/8, 1/12, 1/16,… … …
(a) 39/7
(b) 1/44
(c) 25/6
(d) 25/7
Ans: (b)
Here a 11 = 4 + (11 - 1)4 = 44
So 11th term will be 1/44.
Example 5: A.M and G.M of two numbers is 27 and 26 respectively then H.M is _____
(a) 22.54
(b) 23.54
(c) 25.03
(d) 21.77
Ans: (c)
G² = A.H = 26² = 27 * H
676/27 = H
Harmonic mean = 25.03
Example 6: Find the reciprocal of harmonic mean of two numbers 18 and 37?
(a) 1/15.31
(b) 1/17.43
(c) 1/24.21
(d) 1/20.21
Ans: (c)
HM = 2xy/(x + y)
So x = 18 and y = 37
H.M = (2 * 18 * 37)/(18 + 37)
H.M = 1332/55 = 24.21.
Reciprocal of this = 1/24.21
Example 7: Find the harmonic mean of two numbers 19 and 57?
(a) 25.31
(b) 27.34
(c) 28.50
(d) 24.21
Ans: (c)
HM = 2xy/(x + y)
So x = 19 and y = 57
H.M = (2 * 19 * 57)/(19 + 57)
H M = 2166/76 = 28.50
Example 8: If there are two sets with 150 and 132 as harmonic mean and comprising 25 and 12 observations then the combined harmonic mean....?
(a) 7.85
(b) 9.53
(c) 5.82
(d) None of the above
Ans: (b)
The mean of the reciprocals of the terms = 1/150 and 1/132.
Thus, the total of the reciprocals of the terms in set i = 1/150 × 25 = 1/6
and in set ii = 1/132 × 12 = 1/11
The sum of the reciprocals of all 37 components is 1/6 + 1/11 = 17/66.
Hence their mean is 17/66 ÷ 37 = 9.53.
Example 9: The harmonic mean of 17,22,13,26 will be?
(a) 14.32
(b) 16.76
(c) 17.90
(d) 21.05
Ans: (d)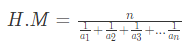
for number 17, 22, 13, 26 harmonic mean is -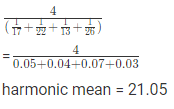
Example 10: Find the harmonic mean of 2 numbers whose G.M. and A.M. is 90 and 75?
(a) 103
(b) 116
(c) 108
(d) 117 Hide
Ans: (c)
GM2 = AM × HM
|
314 videos|170 docs|185 tests
|
FAQs on Solved Examples: Harmonic Progressions - Quantitative Aptitude for SSC CGL
| 1. What is a harmonic progression? |  |
| 2. How can harmonic progressions be identified? |  |
| 3. What is the formula to find the nth term of a harmonic progression? |  |
| 4. Are there any real-life applications of harmonic progressions? |  |
| 5. How can harmonic progressions be used in music composition? |  |
|
314 videos|170 docs|185 tests
|

|
Explore Courses for SSC CGL exam
|

|