Solved Numericals on: Arrhenius Equation, Effect of Temperature on Rate of Reaction | Physical Chemistry PDF Download
Q.1. The rate of a reaction doubles when its temperature changes from 300 K to 310 K. Activation energy of such a reaction will be:
(R = 8.314JK-1 mol−1 log102 = 0.301)
(a) 58.5kJmol−1
(b) 60.5kJmol−1
(c) 53.6kJmol−1
(d) 48.6kJmol−1
Correct Answer is Option (c)
Now 2.303log10
2.303log102 =
= 53.6kJmol−1
Q.2. The rate constants of a reaction at 500K and 700K are 0.02s −1 and 0.07s −1 respectively. Calculate the values of Ea and A:
At 500K , K=0.02s −1
At 700K,k=0.07s −1
Calculation of Ea and A can be done using Arrhenius equation
k=Ae−E a/RT
lnk=lnA +
At 500 K,
ln0.02=lnA+
lnA=ln(0.02)+
At700K
lnA=ln(0.07)+
Equating (1) and (2)
Ea =18227.6J
Ea =18.2KJ
Substituting value of Ea in (1),
=(−3.9120)+4.3848
lnA=0.4728
logA=1.0889
A=antilog(1.0889)
A=12.27
Thus Ea is 18.2 KJ and A is 12.27
Q.3. The rate of the chemical reaction doubles for an increase of 10 K in absolute temperature from 298 K. Calculate Ea.
It is given that T 1 = 298 K
∴T 2 = (298 + 10) K
= 308 K
We also know that the rate of reaction doubles when the temperature is increased by 10 K.
Therefore, let us take the value of k1 = k and that of k2 = 2k
Also, R = 8.314 J K - 1 mol - 1
Now, substituting these values in the equation:E a =52.9kJ mol −1
Q.4. The rate constant is doubled when temperature increases from 27° C to 37° C. Activation energy in kJ is:
(a) 34.2
(b) 58.8
(c) 100.8
(d) 53.6
Correct Answer is Option (d)
We are given that:
When T1 =27+273=300K
Let k1 =k
When T2 =37+273=310K
k2 =2k
Substituting these values the equation:
Ea =53598.6 Jmol −1
Ea =53.6 kJmol −1
Hence, the energy of activation of the reaction is 53.6 kJmol −1
Q.5. The rate constant for the first order decomposition of H2 O2 is given by the following equation:
logk=14.341.25×104 K/T
Calculate Ea for this reaction and at what temperature will its half-period be 256 minutes?
The expression for the rate constant is as follows:
logk=14.34−1.25×104 K/T...(i)
Comparing it with Arrhenius equation, we get-E a
Ea =1.25×10 4 ×2.303×8.314
The activation energy =Ea =239339J/mol=239.339kJ/mol
Half life period, t 1/2 =256min=256×60 sec
k=4.51×10−5/s
Substitute in equation (i), we get-log4.51×10 −5 =14.341.25×104 K/T
−4.35=14.341.25×104 K/T
T=669 K
Hence, the temperature at which the half-life period is 256 minutes is 669 K.
Q.6. What is the effect of temperature on the rate constant of a reaction? How can this effect of temperature on rate constant be represented quantitatively?
With increase in temperature, the rate of the reaction and the rate constant increases. As a generalization, the rate of the reaction (and the rate constant) becomes almost double for every ten degree rise in temperature. This is also called temperature coefficient. It is the ratio of rate constants of the reaction at two temperatures differing by ten degree. Thus,
Q.7. What is the activation energy for a reaction if its rate doubles when the temperature is raised from 20° to 35° ? (R =8.314 J mol-1 K-1)
(a) 269 kJ mol−1
(b) 34.7 kJ mol−1
(c) 15.1 kJ mol−1
(d) 342 kJ mol−1
Correct Answer is Option (b)
Substituting the valuesEa = 34.7 kJ mol−1
Q.8. The activation energy for the reaction 2HI (g) →H2I2(g) is 209.5 209.5mol −1 at 581 K. Calculate the fraction of molecules of reactants having energy equal to or greater than activation energy.
The Arrenhius Equation is given by,
here in this equation Ea is the activation energy and the term
is the fraction of molecules of reactants having energy equal to or greater than activation energy.
Therefore,
finding the value of
we get
Q.9. The rate of a chemical reaction doubles for every 10° C rise of temperature. If the temperature is raised by 50° C, the rate of the reaction increases by about:
(a) 10 times
(b) 24 times
(c) 32 times
(d) 64 times
The rate of a chemical reaction doubles for every 10° C rise of temperature. If the temperature is raised by 50° C, the rate of the reaction increases by about 32 times.
50/10 = 5
25 = 32
Q.10. (a) Derive an integrated rate equation for rate constant of a first order reaction.
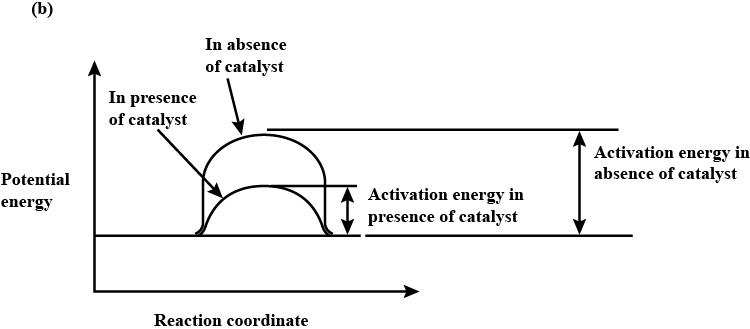
(b) Draw a graph of potential energy V/S reaction co-ordinates showing the effect of catalyst on activation energy (Ea) of a reaction.
(a) Consider a general first order reaction
R → P
The differential rate equation for given reaction can be written as
Rearrange above equation.
Integrating on both sides of the given equation
ln[R]=−Kt+I ..(1)
Where I is Integration constant
At t=0 the concentration of reactant [R]=[R]0 where [R]0 is initial concentration of reactant
Substituting in equation (1) we get
ln [R]0 =(−K×0)+Iln [R]0=I (2)
Substitute I value in equation (1)
In [R] = - Kt + In [R]0
|
83 videos|142 docs|67 tests
|
FAQs on Solved Numericals on: Arrhenius Equation, Effect of Temperature on Rate of Reaction - Physical Chemistry
| 1. What is the Arrhenius equation and how is it used to calculate the rate of reaction at different temperatures? |  |
| 2. How does temperature affect the rate of reaction according to the Arrhenius equation? |  |
| 3. What is the significance of the activation energy (Ea) in the Arrhenius equation? |  |
| 4. How can the Arrhenius equation be used to predict the effect of temperature on the rate of reaction? |  |
| 5. Can the Arrhenius equation be used for all chemical reactions? |  |
























 is the fraction of molecules of reactants having energy equal to or greater than activation energy.
is the fraction of molecules of reactants having energy equal to or greater than activation energy.


 we get
we get