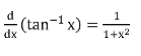Solved examples on Differentiation | Engineering Mathematics - Engineering Mathematics PDF Download
Derivatives of Implicit Functions
The below example explains the method of derivative of implicit functions.
Example 1: Find dy / dx, if y + sin y = cos x
Solution:
dy / dx + cosy . dy / dx = -sin x
dy / dx (1 + cos y) = -sin x n = 0, 1, 2...
n = 0, 1, 2...
Derivatives of Inverse Trigonometric Functions
The below example explains the method of derivative of Inverse Trigonometric functions.
Example 2: Find the value of f’(x) where f(x) = sin-1 x
Solution: Let y = sin-1 x
sin y = x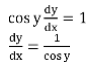
We know, sin2y + cos2y = 1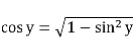
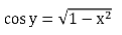
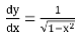
Note:
Logarithmic Differentiation
The below example explains the method of derivative of Logarithmic functions
Example 3: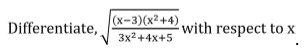
Solution:
Let y = 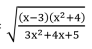
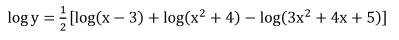
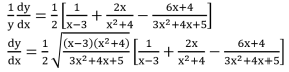
Derivatives of Functions in Parametric Forms
The below example explains the method of derivative functions in parametric form.
Example 4: Find, dy / dx, if x = a(θ + sinθ), y = a(1 - cosθ)
Solution:
dx / dθ = a(1 + cosθ)
dy / dθ = a sin θ
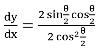
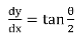
Example 5: Find the value of dy / dx if x2 / 3 + y2 / 3 = a2 / 3
Solution:
Let x = a cos3θ and y = a sin3θ which satisfy the above equation
dx / dθ = -3a cos2θ sin θ
dy / dθ = 3a sin2θ cosθ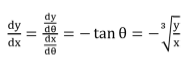
Second Order Derivative
So far we have seen only first order derivatives and second order derivative can be obtained by again differentiating first order differential equation with respect to x.
Let y = f (x) then dy / dx = f' (x) ...........(1)
If f’(x) is differentiable, we may differentiate above equation w.r.t x.
i.e. d / dx (dy / dx) is called the second order derivative of w.r.t x and it is denoted by d2y / dx2
Note:
Let the function f(x) be continuous on [a, b] and differentiable on the open interval (a, b), then
1. f(x) is strictly increasing in [a, b] if f’(x) > 0 for each x (a, b)
2. f(x) is strictly decreasing in [a, b] if f’(x) < 0 for each x (a, b)
3. f(x) is constant function in [a, b] if f’(x) = 0 for each x (a, b)
Example 6: Find the intervals in which the function f is given by
f(x) = sin x + cos x : 0 ≤ x ≤ 2π
is strictly increasing or strictly decreasing.
Solution: We have, f(x) = sin x + cos x f'(x)
= cos x – sin x
Now, f' (x) = 0 gives sin x = cos x which gives that x = π / 4, 5π / 4 in 0 ≤ x ≤ 2π
The point x = π / 4 and x = 5π / 4 divide the interval[0, 2π] into three disjoint intervals
Namely [0, π / 4), (π / 4, 5π / 4) and (5π / 4, 2π]
Note that f’(x) > 0 if x ∈ [0, π / 4) ∪ (5π / 4, 2π] that means f is strictly increasing in this interval
Differentiation by Substitution
Substitution is useful to reduce the function into simple form. For problems involving inverse trigonometric functions, first try for a suitable substitution to simplify it and then differentiate it. If no such substitution is found, then differentiate directly. Some standard substitutions are given below.
| Expressions | Substitutions |
| √a2+x2 | x = atanθ or x = acosθ |
| √a2−x2 | x = asinθ or x = acosθ |
| √x2−a2 | x = asecθ or x = acosecθ |
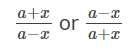 | x = atanθ |
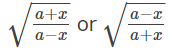 | x = acosθ |
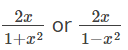 | x = atanθ |
| acosx + bcosx | a = rcosα, b = rsinα |
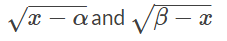 | x = αsin²θ + βcos²θ |
 | x = a(1 – cosθ) |
|
65 videos|129 docs|94 tests
|
FAQs on Solved examples on Differentiation - Engineering Mathematics - Engineering Mathematics
| 1. What is differentiation in mathematics? |  |
| 2. How is differentiation used in real life? |  |
| 3. What are the basic rules of differentiation? |  |
| 4. How is differentiation related to integration? |  |
| 5. What are the applications of differentiation in optimization problems? |  |