Year 11 Exam > Year 11 Notes > Mathematics for GCSE/IGCSE > Solving Linear Inequalities
Solving Linear Inequalities | Mathematics for GCSE/IGCSE - Year 11 PDF Download
| Table of contents |
|
| What is a linear inequality? |
|
| How do I solve linear inequalities? |
|
| How do I represent linear inequalities on a number line? |
|
| How do I solve double inequalities? |
|
What is a linear inequality?
- An inequality indicates that one expression is greater than (>) or less than (<) another.
- ⩾ means "greater than or equal to," and ⩽ means "less than or equal to."
- A Linear Inequality contains only x (and/or y) without x^2 terms or higher powers of x.
- For instance, 3x - 4 ≥ 7 would be interpreted as "3x - 4 is greater than or equal to 7."
How do I solve linear inequalities?
- Solving linear inequalities follows the same principles as solving linear equations, but you must maintain the inequality sign throughout.
- Changing the inequality sign to an equals sign alters the meaning of the problem.
- When you multiply or divide both sides by a negative number, you must reverse the direction of the inequality sign. For example,1 < 2 → [times both sides by (–1)] → –1 > –2 (sign flips)
- Avoid multiplying or dividing by a variable (x) since it could be positive or negative.
- The safest method for rearranging inequalities is to add and subtract terms to consolidate them on one side.
- Understanding how to use number lines and handle "double" inequalities is also crucial.
How do I represent linear inequalities on a number line?
- Inequalities like x < a and x > a can be shown on a regular number line with an open circle at a and an arrow extending to the left for less than and to the right for greater than.
- For inequalities like x ≤ a and x ≥ a, a solid circle at a is used, with an arrow pointing left for less than or equal to and right for greater than or equal to.
- Inequalities such as a < x < b and a ≤ x ≤ b are depicted with two circles at a and b and a line between them.
- For less than or greater than, use open circles.
- For less than or equal to or greater than or equal to, use solid circles.
- Disjoint inequalities like "x < a or x > b" can be shown with two circles at a and b, with an arrowed line extending left from a and right from b, and a gap between a and b.
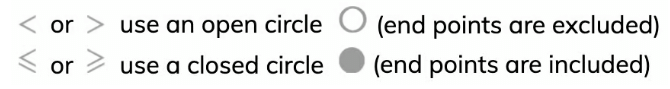
How do I solve double inequalities?
- Inequalities like a < 2x < b are solved by applying the same operation to all three parts of the inequality.
- This follows the same principles as solving linear inequalities.
The document Solving Linear Inequalities | Mathematics for GCSE/IGCSE - Year 11 is a part of the Year 11 Course Mathematics for GCSE/IGCSE.
All you need of Year 11 at this link: Year 11
|
84 videos|120 docs
|
Related Exams
About this Document
|
Dec 22, 2024 Last updated |
Document Description: Solving Linear Inequalities for Year 11 2024 is part of Mathematics for GCSE/IGCSE preparation.
The notes and questions for Solving Linear Inequalities have been prepared according to the Year 11 exam syllabus. Information about Solving Linear Inequalities covers topics
like What is a linear inequality?, How do I solve linear inequalities?, How do I represent linear inequalities on a number line?, How do I solve double inequalities? and Solving Linear Inequalities Example, for Year 11 2024 Exam. Find important definitions, questions, notes, meanings, examples, exercises and tests below for Solving Linear Inequalities.
Introduction of Solving Linear Inequalities in English is available as part of our Mathematics for GCSE/IGCSE
for Year 11 & Solving Linear Inequalities in Hindi for Mathematics for GCSE/IGCSE course.
Download more important topics related with notes, lectures and mock test series for Year 11
Exam by signing up for free. Year 11: Solving Linear Inequalities | Mathematics for GCSE/IGCSE - Year 11
Description
Full syllabus notes, lecture & questions for Solving Linear Inequalities | Mathematics for GCSE/IGCSE - Year 11 - Year 11 | Plus excerises question with solution to help you revise complete syllabus for Mathematics for GCSE/IGCSE | Best notes, free PDF download
Information about Solving Linear Inequalities
In this doc you can find the meaning of Solving Linear Inequalities defined & explained in the simplest way possible. Besides explaining types of
Solving Linear Inequalities theory, EduRev gives you an ample number of questions to practice Solving Linear Inequalities tests, examples and also practice Year 11
tests
|
Explore Courses for Year 11 exam
|
|
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.
Related Searches
Viva Questions
,MCQs
,Solving Linear Inequalities | Mathematics for GCSE/IGCSE - Year 11
,Sample Paper
,Semester Notes
,mock tests for examination
,Summary
,Objective type Questions
,shortcuts and tricks
,Important questions
,practice quizzes
,Exam
,Solving Linear Inequalities | Mathematics for GCSE/IGCSE - Year 11
,Solving Linear Inequalities | Mathematics for GCSE/IGCSE - Year 11
,study material
,Free
,ppt
,past year papers
,Previous Year Questions with Solutions
,video lectures
,Extra Questions
;
Additional Information about Solving Linear Inequalities for Year 11 Preparation
Solving Linear Inequalities Free PDF Download
The Solving Linear Inequalities is an invaluable resource that delves deep into the core of the Year 11 exam.
These study notes are curated by experts and cover all the essential topics and concepts, making your preparation more efficient and effective.
With the help of these notes, you can grasp complex subjects quickly, revise important points easily,
and reinforce your understanding of key concepts. The study notes are presented in a concise and easy-to-understand manner,
allowing you to optimize your learning process. Whether you're looking for best-recommended books, sample papers, study material,
or toppers' notes, this PDF has got you covered. Download the Solving Linear Inequalities now and kickstart your journey towards success in the Year 11 exam.
Importance of Solving Linear Inequalities
The importance of Solving Linear Inequalities cannot be overstated, especially for Year 11 aspirants.
This document holds the key to success in the Year 11 exam.
It offers a detailed understanding of the concept, providing invaluable insights into the topic.
By knowing the concepts well in advance, students can plan their preparation effectively.
Utilize this indispensable guide for a well-rounded preparation and achieve your desired results.
Solving Linear Inequalities Notes
Solving Linear Inequalities Notes offer in-depth insights into the specific topic to help you master it with ease.
This comprehensive document covers all aspects related to Solving Linear Inequalities.
It includes detailed information about the exam syllabus, recommended books, and study materials for a well-rounded preparation.
Practice papers and question papers enable you to assess your progress effectively.
Additionally, the paper analysis provides valuable tips for tackling the exam strategically.
Access to Toppers' notes gives you an edge in understanding complex concepts.
Whether you're a beginner or aiming for advanced proficiency, Solving Linear Inequalities Notes on EduRev are your ultimate resource for success.
Solving Linear Inequalities Year 11 Questions
The "Solving Linear Inequalities Year 11 Questions" guide is a valuable resource for all aspiring students preparing for the
Year 11 exam. It focuses on providing a wide range of practice questions to help students gauge
their understanding of the exam topics. These questions cover the entire syllabus, ensuring comprehensive preparation.
The guide includes previous years' question papers for students to familiarize themselves with the exam's format and difficulty level.
Additionally, it offers subject-specific question banks, allowing students to focus on weak areas and improve their performance.
Study Solving Linear Inequalities on the App
Students of Year 11 can study Solving Linear Inequalities alongwith tests & analysis from the EduRev app,
which will help them while preparing for their exam. Apart from the Solving Linear Inequalities,
students can also utilize the EduRev App for other study materials such as previous year question papers, syllabus, important questions, etc.
The EduRev App will make your learning easier as you can access it from anywhere you want.
The content of Solving Linear Inequalities is prepared as per the latest Year 11 syllabus.
|
© EduRev
|
Education Revolution
|
|
Signup to see your scores
go up within 7 days!
Access 1000+ FREE Docs, Videos and Tests
Takes less than 10 seconds to signup