Sorting Algorithms- 1 | Algorithms - Computer Science Engineering (CSE) PDF Download
Selection Sort
The selection sort algorithm sorts an array by repeatedly finding the minimum element (considering ascending order) from unsorted part and putting it at the beginning. The algorithm maintains two subarrays in a given array.
- The subarray which is already sorted.
- Remaining subarray which is unsorted.
In every iteration of selection sort, the minimum element (considering ascending order) from the unsorted subarray is picked and moved to the sorted subarray.
Following example explains the above steps:
arr[] = 64 25 12 22 11
// Find the minimum element in arr[0...4]
// and place it at beginning
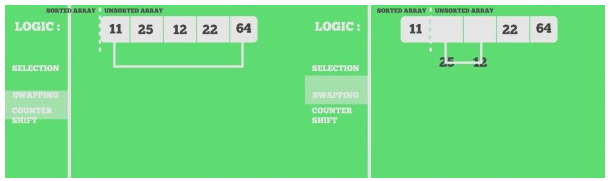
11 25 12 22 64
// Find the minimum element in arr[1...4]
// and place it at beginning of arr[1...4]
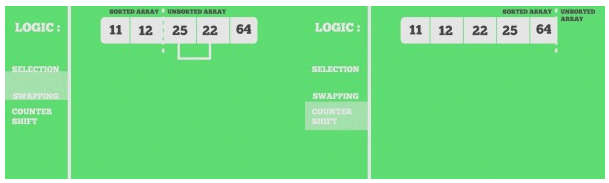
11 12 25 22 64
// Find the minimum element in arr[2...4]
// and place it at beginning of arr[2...4]
11 12 22 25 64
// Find the minimum element in arr[3...4]
// and place it at beginning of arr[3...4]
11 12 22 25 64
Flowchart of the Selection Sort: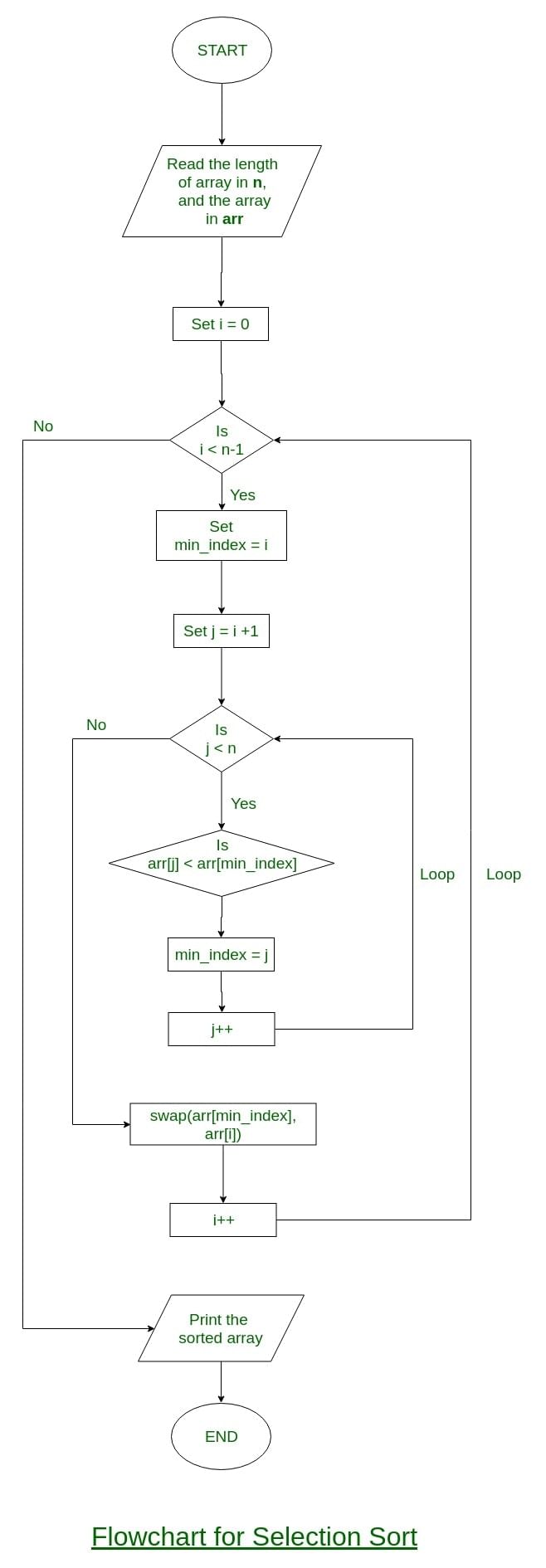
- C++
// C++ program for implementation of selection sort
#include <bits/stdc++.h>
using namespace std;
void swap(int *xp, int *yp)
{
int temp = *xp;
*xp = *yp;
*yp = temp;
}
void selectionSort(int arr[], int n)
{
int i, j, min_idx;
// One by one move boundary of unsorted subarray
for (i = 0; i < n-1; i++)
{
// Find the minimum element in unsorted array
min_idx = i;
for (j = i+1; j < n; j++)
if (arr[j] < arr[min_idx])
min_idx = j;
// Swap the found minimum element with the first element
swap(&arr[min_idx], &arr[i]);
}
}
/* Function to print an array */
void printArray(int arr[], int size)
{
int i;
for (i=0; i < size; i++)
cout << arr[i] << " ";
cout << endl;
}
// Driver program to test above functions
int main()
{
int arr[] = {64, 25, 12, 22, 11};
int n = sizeof(arr)/sizeof(arr[0]);
selectionSort(arr, n);
cout << "Sorted array: \n";
printArray(arr, n);
return 0;
}
// This is code is contributed by rathbhupendra - C
// C program for implementation of selection sort
#include <stdio.h>
void swap(int *xp, int *yp)
{
int temp = *xp;
*xp = *yp;
*yp = temp;
}
void selectionSort(int arr[], int n)
{
int i, j, min_idx;
// One by one move boundary of unsorted subarray
for (i = 0; i < n-1; i++)
{
// Find the minimum element in unsorted array
min_idx = i;
for (j = i+1; j < n; j++)
if (arr[j] < arr[min_idx])
min_idx = j;
// Swap the found minimum element with the first element
swap(&arr[min_idx], &arr[i]);
}
}
/* Function to print an array */
void printArray(int arr[], int size)
{
int i;
for (i=0; i < size; i++)
printf("%d ", arr[i]);
printf("\n");
}
// Driver program to test above functions
int main()
{
int arr[] = {64, 25, 12, 22, 11};
int n = sizeof(arr)/sizeof(arr[0]);
selectionSort(arr, n);
printf("Sorted array: \n");
printArray(arr, n);
return 0;
} - Python
# Python program for implementation of Selection
# Sort
import sys
A = [64, 25, 12, 22, 11]
# Traverse through all array elements
for i in range(len(A)):
# Find the minimum element in remaining
# unsorted array
min_idx = i
for j in range(i+1, len(A)):
if A[min_idx] > A[j]:
min_idx = j
# Swap the found minimum element with
# the first element
A[i], A[min_idx] = A[min_idx], A[i]
# Driver code to test above
print ("Sorted array")
for i in range(len(A)):
print("%d" %A[i]), - Java
// Java program for implementation of Selection Sort
class SelectionSort
{
void sort(int arr[])
{
int n = arr.length;
// One by one move boundary of unsorted subarray
for (int i = 0; i < n-1; i++)
{
// Find the minimum element in unsorted array
int min_idx = i;
for (int j = i+1; j < n; j++)
if (arr[j] < arr[min_idx])
min_idx = j;
// Swap the found minimum element with the first
// element
int temp = arr[min_idx];
arr[min_idx] = arr[i];
arr[i] = temp;
}
}
// Prints the array
void printArray(int arr[])
{
int n = arr.length;
for (int i=0; i<n; ++i)
System.out.print(arr[i]+" ");
System.out.println();
}
// Driver code to test above
public static void main(String args[])
{
SelectionSort ob = new SelectionSort();
int arr[] = {64,25,12,22,11};
ob.sort(arr);
System.out.println("Sorted array");
ob.printArray(arr);
}
}
/* This code is contributed by Rajat Mishra*/ - C#
// C# program for implementation
// of Selection Sort
using System;
class GFG
{
static void sort(int []arr)
{
int n = arr.Length;
// One by one move boundary of unsorted subarray
for (int i = 0; i < n - 1; i++)
{
// Find the minimum element in unsorted array
int min_idx = i;
for (int j = i + 1; j < n; j++)
if (arr[j] < arr[min_idx])
min_idx = j;
// Swap the found minimum element with the first
// element
int temp = arr[min_idx];
arr[min_idx] = arr[i];
arr[i] = temp;
}
}
// Prints the array
static void printArray(int []arr)
{
int n = arr.Length;
for (int i=0; i<n; ++i)
Console.Write(arr[i]+" ");
Console.WriteLine();
}
// Driver code
public static void Main()
{
int []arr = {64,25,12,22,11};
sort(arr);
Console.WriteLine("Sorted array");
printArray(arr);
}
}
// This code is contributed by Sam007 - PHP
<?php
// PHP program for implementation
// of selection sort
function selection_sort(&$arr, $n)
{
for($i = 0; $i < $n ; $i++)
{
$low = $i;
for($j = $i + 1; $j < $n ; $j++)
{
if ($arr[$j] < $arr[$low])
{
$low = $j;
}
}
// swap the minimum value to $ith node
if ($arr[$i] > $arr[$low]
{
$tmp = $arr[$i];
$arr[$i] = $arr[$low];
$arr[$low] = $tmp;
}
}
}
// Driver Code
$arr = array(64, 25, 12, 22, 11);
$len = count($arr);
selection_sort($arr, $len);
echo "Sorted array : \n";
for ($i = 0; $i < $len; $i++)
echo $arr[$i] . " ";
// This code is contributed
// by Deepika Gupta.
?>
Output:
Sorted array:
11 12 22 25 64
Time Complexity: O(n2) as there are two nested loops.
Auxiliary Space: O(1)
The good thing about selection sort is it never makes more than O(n) swaps and can be useful when memory write is a costly operation.
Stability: The default implementation is not stable. However it can be made stable. Please see stable selection sort for details.
In Place: Yes, it does not require extra space.
Snapshots: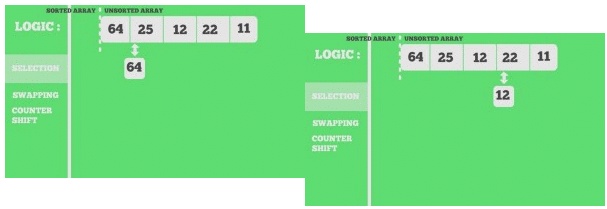
Quiz on Selection Sort
Other Sorting Algorithms on GeeksforGeeks/GeeksQuiz:
- Bubble Sort
- Insertion Sort
- Merge Sort
- Heap Sort
- QuickSort
- Radix Sort
- Counting Sort
- Bucket Sort
- ShellSort
|
81 videos|80 docs|33 tests
|
FAQs on Sorting Algorithms- 1 - Algorithms - Computer Science Engineering (CSE)
| 1. What is selection sort and how does it work? |  |
| 2. What is the time complexity of selection sort? |  |
| 3. Is selection sort stable? |  |
| 4. When is selection sort a good choice for sorting? |  |
| 5. Can selection sort be used for sorting in descending order? |  |

|
Explore Courses for Computer Science Engineering (CSE) exam
|

|

















