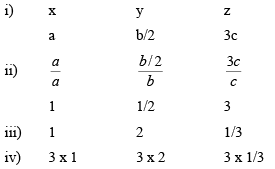Space Lattice | Solid State Physics, Devices & Electronics PDF Download
Introduction
Introduction
Introduction
A space lattice is defined as “an infinite array of points in three dimensional space in which each point is identically located with respect to other”. It is a periodic arrangement of points arranged in regular manner and having repeat distance in three directions which are termed as “fundamental lattice vectors”. If at these lattice positions, we place atom, or group of two, three etc atoms we obtained a crystalline solid.
Let us now consider the case of a two dimensional array of points as shown in figure (i).
A two-dimensional array may have (a) square (b) rectangular array. 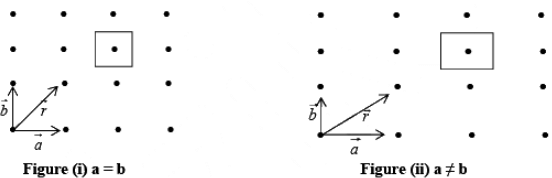
In figure (i) and (ii)  are fundamental translational vectors, and
are fundamental translational vectors, and 
is generated vector. If points are located such that 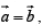 , the arrangement will be known as square lattice, if location of the point is such that a ≠ b figure (ii) the arrangement will be called rectangular lattice.
, the arrangement will be known as square lattice, if location of the point is such that a ≠ b figure (ii) the arrangement will be called rectangular lattice.
Translation and Primitive Translation Vector
A three dimensional space lattice may have
1. Cubic array when a = b = c
2. Non-cubic array
a lattice exhibit perfect translational symmetry and relative to an arbitrary chosen origin at a lattice pint, any other lattice point has the position vector 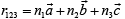 where n1, n2, n3, are arbitrary integers
where n1, n2, n3, are arbitrary integers 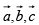 are fundamental units of the translational symmetry.
are fundamental units of the translational symmetry.
Considering first the translational vector a1 and b1 the point R' can be obtained from R using the translational operator (T = n1a + n2b) given by
T = 0a1 + 1b1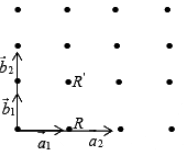
Which containing integer coefficients, thus R' is related to R by the equation
R' = R + T = R + 0a1 + 1b1,
Such translational vector which produced a translational operation containing coefficient integer coefficient called primitive translation vectors, referring to the second set of translation vector a2 and b2 the point R' can be obtained from R by using the equation
R' = R + (1/2)a2 + (1/2)b2
Which containing non-integral coefficient of a2 and b2 such translation vector for which the translation operation contains non-integral coefficient are called non-primitive translation vectors.
➤ Unit cells
The entire lattice structure of a crystal can be generated by identical blocks known as unit cell. The unit cell may be a group of ions, atoms or molecules. The unit cell is the smallest building block or geometric figure from which the crystal is built up by repeating it in three dimensions as shown below.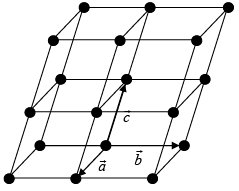
➤ Primitive and Non Primitive Unit Cells
A unit cell can be chosen in a number of ways. The following figure shows two ways of choosing a unit cell in two dimensions. In the first way the unit cell contains lattice points only at the corners. This type of unit cells is called as Primitive Cells. In the second way the unit cell contains lattice points in addition to the corners. These are known as Non Primitive Cells.
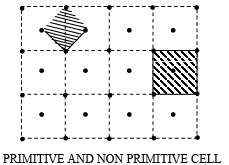
Note: The unit cells differ from the primitive cell in that it is not restricted to being the equivalent of one lattice point. Thus, unit cells may also be primitive cells, but all the primitive cells need not be Unit Cells. The unit cell is so-called because the entire lattice can be derived by repeating this cell as a unit by means of the translations that serve as the unit cell’s edge. In three dimension there are four type of possible unit cells.
- Primitive (P-type)
It has lattice point only at corners and each corner is common in eight cells, so each cell represents a single lattice point 8 x (1/8) = 1 lattice point /unit cell as shown in
figure.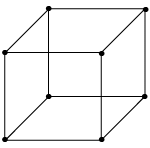
- Body Centered cell (I-type)
It has lattice points at corners as well as at centre of each cell, so each cell has two lattice points per unit cell.
8 x (1/8) + 1 = 1 + 1 = 2 lattice point /unit cell.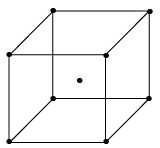
- Face Centered cell (F-type)
It has a lattice point at corner as well as at centre of each face of the cell as shown in figure.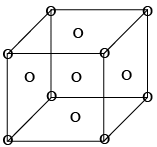 8 x (1/8) + 6 x (1/2) = 1 + 3 = 4 lattice point /unit cell.
8 x (1/8) + 6 x (1/2) = 1 + 3 = 4 lattice point /unit cell. - Base Centred (C-type)
It has lattice points at corner as well as centre of top and bottom face of cell, it has two lattice points per unit cell as shown in figure: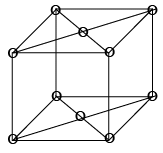 8 x (1/8) + 2 x (1/2) = 1 + 1 = 2
8 x (1/8) + 2 x (1/2) = 1 + 1 = 2
➤ Wigner-Seitz Cell
The primitive cell can also be constructed using the following procedure
(i) Connect a given lattice point to all the nearby lattice points.
(ii) Draw normal at the mid point of lines connecting the lattice points.
The smallest volume enclosed by the normal is the required primitive cell, such a cell is Wigner-Seitz cell
Basis
The repeating unit assembly: atom, molecule, ion or radical that is located at each lattice point is called basis or motif. Every basis is identical in composition, arrangement and orientation, when the basis is repeated with correct periodically in all directions, it gives the actually crystal structure, the crystal structural is real, while the lattice is imaginary.
Thus,
Lattice + Basis = Crystal structure
Figure shows the basis representing each lattice point. It is observed from the figure that a basis consists of three different atoms.
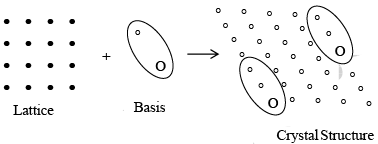
More precisely we can say that when the space lattice combines with the basis a unit cell of the crystal is generated, the unit cell will be called ‘monoatomic’ if one atom occupies a lattice point. When two atoms occupy a lattice point, it will make a diatomic unit cell. Similarly, the unit cell will be known as multiatomic when too many occupy a lattice point.
Eg: Cu Crystal is a Mono-atomic crystal; NaCl is a diatomic crystal while CaF2 is a tri-atomic crystal.
➤ Symmetry Operation
A symmetry operation is that which transforms the crystal to itself, i.e. a crystal remains invariant under a symmetry operation. These operations are:
(i) Translational
(ii) Rotational
(iii) Reflection
(iv) Inversion.
- Translations: The translation symmetry follows from the orderly arrangement of a lattice. It means that a lattice point r, under lattice translation vector operator T, gives another point r' which is exactly identical r' = r + T.
- Rotations: A lattice is said to posses the rotation symmetry if its rotation by an angle θ about an axis (or a point in a two dimensional lattice) transforms the lattice to itself. Also, since the lattice always remains invariant by a rotation of 2 π, the angle 2π must be an integer multiple of θ i.e. nθ = 2π the factor n takes integral values and is known as multiplicity of rotation axis. The possible value of n which are compatible with the requirement of translation symmetry are 1, 2, 3, 4, 6 only. But 5 fold, 7 fold or higher order symmetry are not possible.
Eg: Hexagonal crystal have 6 fold axis of rotation θ = 360/60 = 60o
Now we can explain why five fold symmetry is not permissible
As we know that the throw of an axis θ = 60 (n fold of the axis) if we consider a regular pentagon, which has an angle of 108o. As 360o is not an integer multiple of 108o pentagons can not be made to meet at a point bearing a constant angle to another. Hence 5 fold symmetry (i.e. a pentagonal lattice) is not possible. Let us consider the row lattice as shown in figure and place an n fold axis at each lattice point.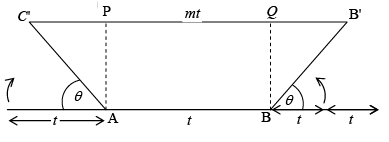 Two opposite rotations by an amount Q about two axis produces two new lattice point C' and B' (and AC' = BB' = t). Therefore, the line joining C' and B' is parallel to the translation t.
Two opposite rotations by an amount Q about two axis produces two new lattice point C' and B' (and AC' = BB' = t). Therefore, the line joining C' and B' is parallel to the translation t.
C'B' = C'P + PQ + QB'
mt = t cos θ + t + t + t cosθ or mt = t (1 + 2 cos θ)
cosθ = (m-1)/2 θ = cos-1(m-1)/2 Let m – 1 = N (Integer)
θ = cos-1(N/2) ∴cosθ = N/2 -2≤N≤2 (∵ cosθ varies from 1 to - 1 )
throw of an axis θ = 2π/n = 3600/n where n is fold of the axis
when N = - 2 cos θ = -1 θ = 180o n = 360/180 = 2
N = - 1 cos θ = -1/2 θ = 120o n = 360/120 = 3
N = 0 cos θ = 0 θ = 90o n = 360/90 = 4
N = + 1 cos θ = 1/2 θ = 60o n = 360/60 = 6
N = + 2 cos θ = + 1 θ = 360o n = 360/360 = 1
Therefore, 2, 3, 4, 6 and 1 fold of symmetry axis are possible, 5 fold symmetry and more than 6 fold is not possible. - Reflections: A lattice is said to possess reflection symmetry if there exists a plane (or a line in two dimensions) in the lattice which divide it into two identical halves which are mirror image of each other. Such a plane is represented by m.
- Inversion: Inversion is a point operation which is applicable to three dimensional lattice only. This symmetry element implies that each point located at r relative to the same lattice point. In other words, it means that the lattice possesses a centre of inversion denoted by 1.
➤ Symmetry Element of Cubic Lattice
Total symmetry elements is cubic lattice is 23.
The geometric locus about which a group of repeating operation acts is called symmetry elements. For example, in square lattice axis normal to the plane of paper about which square is rotated by 900, 1800 and 2700 to preserve the symmetry is a symmetry element. In square lattice, axis in the plane of paper and bisecting the opposite edges of the square which rotate the square by 1800 to preserve symmetry is called another symmetry element. Similarly the plane across which the reflection occurs is a symmetry element and called a reflection plane or a mirror etc. In cubic lattice there are total 13 rotational symmetry elements (3 tetrad axis Fig.c , 4 triad axis Fig d and 6 diad axis Fig e), 9 reflection symmetry elements, a plane of symmetry parallel to the face of the cube and diagonal to the cube is shown in fig a and fig b, and there is only 1 inversion symmetry elements. 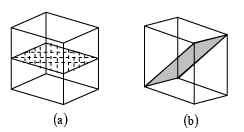
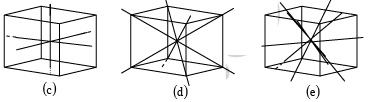
Bravais Space Lattice
There are number of ways in which an actual crystal may be built up and atoms piled together resulting in a great many crystal structures. But each of the structure consists of some fundamental patterns repeated at each point of a space lattice. The scheme of repetitions of a space lattice are very limited in number while the possible crystal structures are almost unlimited. But it was shown by Bravais that there are 14 different arrays or networks of lattice in which points can be arranged in space so that each point has identical surrounding these are known as Bravais Space Lattice.
Bravais Lattice: These are 5 in 2-Dimension and 14 in 3-Dimension
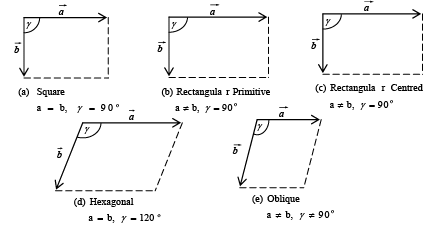
➤ Bravais Lattices in Two-Dimension
The four crystal systems of two-dimensional space are square, rectangular, hexagonal, and oblique. The rectangular crystal system has two Bravais lattice namely rectangular primitive and rectangular centred. In all there are five Bravais lattices: 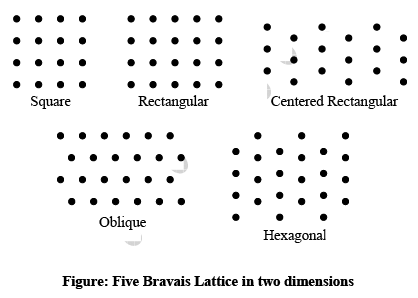
➤ Bravais Lattices in three-dimension: In three dimension Bravais lattice is given as 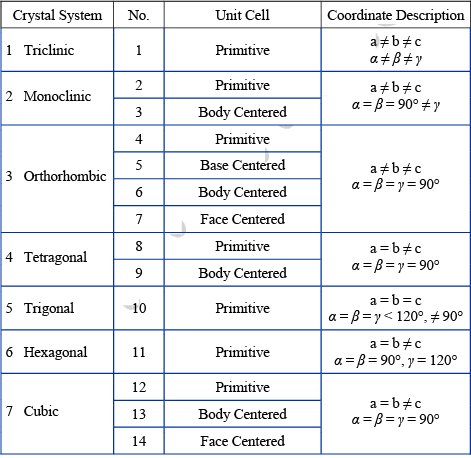
➤ Lattice Parameters
To completely illustrate the crystal structure, the basic minimum parameters required are:
(1) The inter atomic or intermolecular distance in x, y and z direction (a, b and c).
(2) The angles (α , β andγ) between the x and y, y and z and z and x axes.
The angle between the x and y axes is taken as α , the angle between the y and z axes is taken as β, angle between the Z and x axes is taken as γ are called the crystal parameters.
Therefore, the acceptable way to study structure of crystals is in terms of interlattice distances and the inter-planar angles, i.e. in terms of the crystal parameters.
➤ Line Indices in a Crystal Lattice
While dealing with a crystal system, it is necessary to refer to the crystal planes, and directions of the straight lines joining the lattice points in a space lattice. A notation system which uses a set of three integers (n1, n2 & n3) is adopted to describe both the positions of planes or directions within the lattice.
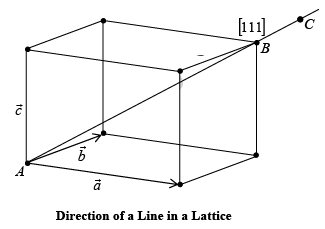
A resultant vector 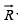 which joins Lattice points A and B can be represented by an Equation.
which joins Lattice points A and B can be represented by an Equation.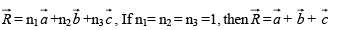
Miller Indices in Crystal Lattice
The crystal lattice may be regarded as made up of an aggregate of a set parallel equidistance planes. For a given lattice, the lattice planes can be chosen in different ways. Miller devised a scheme for indexing lattice planes by integers. These indices are known as the miller indices of the lattice planes.
The steps in the determination of miller indices of a plane are illustrated with the help of figure.
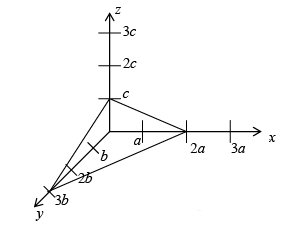
➤ Step:
- Determination the co-ordinate of the intercepts made by the plane along the three crystallographic axes (x, y, z)
For example: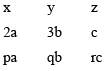
with p = 2 q = 3 r = 1 - Express the Intercepts as multiples of the unit cell dimensions, or lattice parameters along axes
i.e.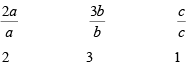
- Get the reciprocals of these numbers
1/2 1/3 1/1 - Reduce these reciprocals to the smallest set of Integer numbers and enclosed them in bracket
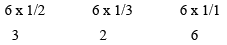
In general it is denoted by (hkl), (326)
Hence, the miller indices are the three smallest possible integers which have the same ratios as the reciprocal of the intercepts of the plane concerned on the three axes.
➤ Important Points
- A zero miller indices indicate that the plane is parallel to the corresponding crystal axis, eg: (130) means the plane is parallel to the z-axis (001) means the plane is parallel to the x and y-axis. Figure shows the miller indices (100), (110), (111).
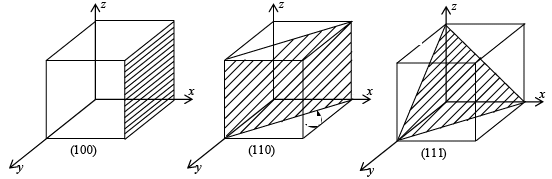
- A negative miller indices shows that the plane (hkl ) cuts the x-axis on the negative side of the origin, eg (100)
- Miller indices represent a family of parallel planes. (200) and (100) are parallel planes.
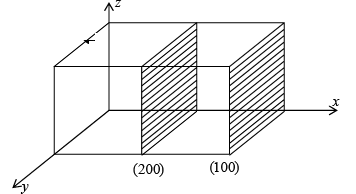
- {} brackets are used to represent all sets of a family of planes. Ex: {100} represents (100), (010), (001) and (100), (010), (001)
- When the integers used in the miller indices contain more than one digit, the indices must be separated by commas for clarity Ex: (3, 11, 13)
Example 1: Obtain the Miller indices of a plane which intercepts at – a, b/2, 3c in a simple cubic unit cell.
Miller indices are (361)Eg: A plane makes intercepts of 1, 2 and 3 Å on the crystallograph i.e. axes of an orthorhombic crystal with a : b : c = 3 : 2 : 1. Determine the miller indices of this plane.
Example 2: The miller indices of a plane in a simple cubic lattice crystal are (123). Get the co-ordinates of the plane
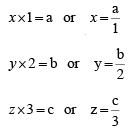
Thus, the co-ordinates of the plane are a, b/2, c/3.
➤ Inter-planar Spacing ( dhkl)
To get the inter-planar distance, consider a plane ABC with Miller indices (hkl). In the reference frame, draw a normal to the plane from the origin. Let OP is the normal to the plane ABC. Let angle POA = α’, and POB = β’ and POC =γ’ be the angles made by the normal to the plane with the x, y and the z directions. OP = d is the interplanar distance
Then, from the figure,
Cos α = ON/OA = d/x
Cos β = ON/OB = d/y
Cos γ = ON/OC = d/z
But from the definition of Millers incise derived in the earlier section,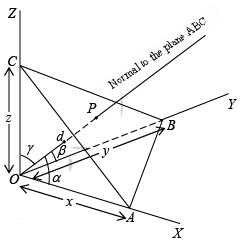
h = a/x therefore, x = a/h
k = b/y therefore, y=b/k
l = c/z therefore z= c/l
Writing the values of x, y and z in the above trigonometric equations we get,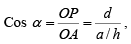
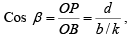
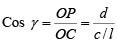
From solid geometry, Cos2 α + cos2 β + Cos2 γ =1
Substituting the values of the trigonometric relations we get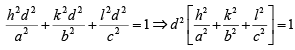
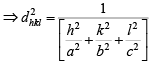
Then, the inter-planar distance ‘d’ is given by 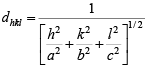
case I: Cubic crystal a = b = c 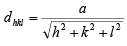
case II: tetragonal a = b ≠ c 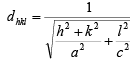
case III: orthorhombic a ≠ b ≠ c 
Density of Crystal
Density is a macroscopic property. Basically it is the mass per unit volume. In case of crystals, mass of atoms packed in a conventional unit cell per unit volume of the cell gives the density of the crystal.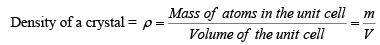
Here m is the mass of atoms packed in the conventional unit cell of the crystal. V is the volume of the unit cell. Mass of atoms packed in the conventional unit cell of the crystal. V is the volume of the unit cell. Mass of an atom in the structure is given by the ratio of the atomic weight or Molecular weight (M) to the Avogadro number (NA). Mass of atoms contained in the conventional unit cell is then the number of atoms in the unit cell times the mass of an atom. If there are neff atoms in the conventional unit cell, then, the mass of atoms in the unit cell is given by
From density equation, mass of atoms in the unit cell in terms of the density of the crystal is given by
m = ρ V
From this equation, the density of the crystal is 
In case of a cubic lattice the volume of the unit cell V = a3
Therefore 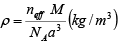
The lattice constant 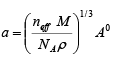
|
91 videos|21 docs|25 tests
|
FAQs on Space Lattice - Solid State Physics, Devices & Electronics
| 1. What is a space lattice in the context of IIT JAM? |  |
| 2. How is a space lattice different from a crystal structure in IIT JAM? |  |
| 3. What are the characteristics of a space lattice in IIT JAM? |  |
| 4. How are space lattices classified in IIT JAM? |  |
| 5. How are space lattices important in IIT JAM? |  |