Spanning Tree | Programming and Data Structures - Computer Science Engineering (CSE) PDF Download

Spanning Tree and Minimum Spanning Tree

In this tutorial, you will learn about spanning tree and minimum spanning tree with help of examples and figures.
Before we learn about spanning trees, we need to understand two graphs: undirected graphs and connected graphs.
An undirected graph is a graph in which the edges do not point in any direction (ie. the edges are bidirectional).

Undirected Graph

A connected graph is a graph in which there is always a path from a vertex to any other vertex.

Connected Graph

Spanning tree

A spanning tree is a sub-graph of an undirected connected graph, which includes all the vertices of the graph with a minimum possible number of edges. If a vertex is missed, then it is not a spanning tree.
The edges may or may not have weights assigned to them.
The total number of spanning trees with n vertices that can be created from a complete graph is equal to n^(n-2).
If we have n = 4, the maximum number of possible spanning trees is equal to 4^4-2 = 16. Thus, 16 spanning trees can be formed from a complete graph with 4 vertices.

Example of a Spanning Tree
Let's understand the spanning tree with examples below:
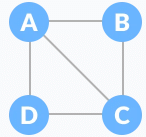
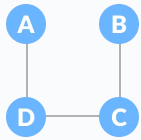
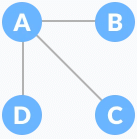
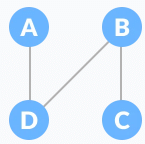
Let the original graph be: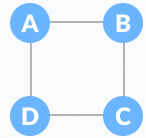
Normal graphSome of the possible spanning trees that can be created from the above graph are:

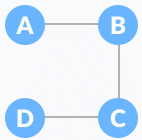
A spanning tree

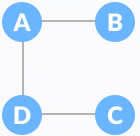
Minimum Spanning Tree
A minimum spanning tree is a spanning tree in which the sum of the weight of the edges is as minimum as possible.

Example of a Spanning Tree
Let's understand the above definition with the help of the example below.
The initial graph is:

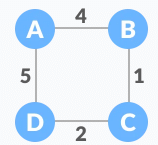Weighted graphThe possible spanning trees from the above graph are:
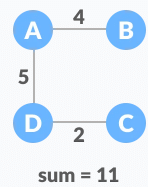Minimum spanning tree - 1

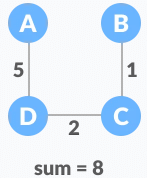Minimum spanning tree - 2

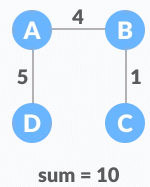Minimum spanning tree - 3

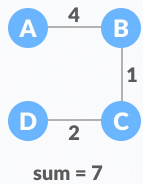Minimum spanning tree - 4

The minimum spanning tree from the above spanning trees is: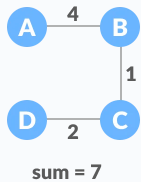
Minimum spanning tree

The minimum spanning tree from a graph is found using the following algorithms:

1. Prim's Algorithm
2. Kruskal's Algorithm

Spanning Tree Applications

• Computer Network Routing Protocol
• Cluster Analysis
• Civil Network Planning

Minimum Spanning tree Applications

• To find paths in the map
• To design networks like telecommunication networks, water supply networks, and electrical grids.