Stability of Floating Bodies | Fluid Mechanics for Mechanical Engineering PDF Download
| Table of contents |

|
| What is Buoyancy ? |

|
| Metacentre |

|
| Stability of a Submerged Body |

|
| Stability of Floating Body |

|
| Oscillation (Rolling) of a Floating Body |

|
| Solved Numericals |

|
What is Buoyancy ?
When an object is submerged in a fluid, the fluid exerts an upward force on the object. This force, known as buoyancy, is equal to the weight of the displaced fluid.Centre of Buoyancy
The centre of buoyancy is the point where the buoyant force is considered to act. Since buoyancy acts vertically and equals the weight of the displaced fluid, the centre of buoyancy coincides with the centre of gravity of the displaced fluid.
Metacentre
The metacentre is the point around which a body begins to oscillate when it is tilted slightly. Alternatively, it can be defined as the point where the line of action of the buoyant force intersects the normal axis of the body after a small angular displacement.Consider a body floating in a liquid as shown in fig. (a). let the body is in equilibrium and G is the centre of gravity and B the centre buoyancy. For equilibrium, both the points lie on the normal axis which is vertical.
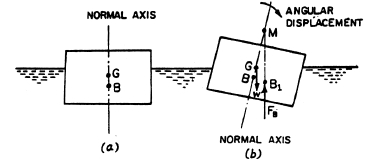
Let the body is given a small angular displacement in the clockwise direction as shown in fig. (b).The centre of buoyancy, which is the centre of gravity of the displaced liquid or centre of gravity of the portion of the body sub − merged in liquid, will now be shifted towards right from the normal axis. Let it is at B1 as shown in Fig. (b).
The line of action of the force of buoyancy in this new position, will intersect the normal axis of the body at some point say M. This point is called Metacentre.
Metacentric Height:
The distance MG, i.e. the distance between the metacentre of a floating body and the centre of gravity of the body is called metacentric height.
Expression for Metacentric Height:
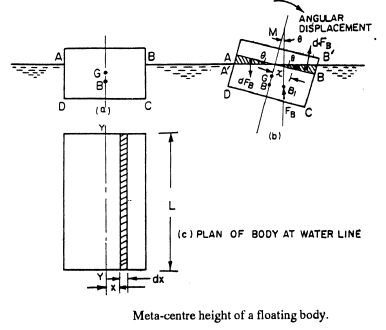 Fig. (a) shows the position of a floating body in equilibrium. The location of centre of gravity and centric of buoyancy in this position is at G and B. The floating body is given a small angular displacement in the clockwise direction. This is shown in fig. (b). The new centre of buoyancy is at B1. The vertical line through B1 cuts the normal axis at M. Hence M is the metacentre and GM is metacentre height.
Fig. (a) shows the position of a floating body in equilibrium. The location of centre of gravity and centric of buoyancy in this position is at G and B. The floating body is given a small angular displacement in the clockwise direction. This is shown in fig. (b). The new centre of buoyancy is at B1. The vertical line through B1 cuts the normal axis at M. Hence M is the metacentre and GM is metacentre height.
Metacentric height = GM = − I/V - BGV
Where;
V = Volume of the fluid displaced by the body.
= Volume of the body submerged in water.
I = Second moment of area of the plan of the body at water surface about the axis y − y .
Stability of Floating and Submerged Bodies: A submerged or a floating body is said to be stable if it comes back to its original position after a slight disturbance. The relative position of the centre of gravity (G) and centre of buoyancy (B1) of a body determines the stability of a submerged body
Stability of a Submerged Body
In the case of a completely submerged body, the positions of the centre of gravity (G) and centre of buoyancy (B) are fixed. Consider a balloon submerged in air where the lower portion contains heavier material, causing its centre of gravity (G) to be lower than its centre of buoyancy (B), as illustrated in Fig. (a). Let the weight of the balloon be W.For the balloon to be in equilibrium, the weight W acts vertically downward through G, and the buoyant force FB acts vertically upward through B. Therefore, W = FB.
If the balloon is tilted clockwise from its original position (Fig. (a)), a couple is formed between W and FB, exerting an anti-clockwise moment. This couple restores the balloon to its original position, indicating that the balloon in the configuration shown in Fig. (a) is in stable equilibrium.
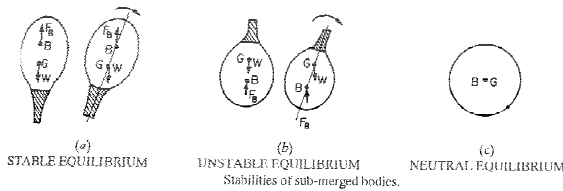
(a) Stable E quilibrium: When W = FB and point B is above G, the body is said to be in stable equilibrium.
(b) Unstable E quilibrium: If W = FB, but the centre of buoyancy (B) is below centre of gravity (G), the body is in unstable equilibrium as shown in Fig. (b). A slight displacement to the body, in the clockwise direction, gives the couple due to W and FB also in the clock wise direction, Thus the body does not return to its original position and hence the body is unstable equilibrium.
(c) Neutral Equilibrium: If FB = W and B and G are at the same point, as shown in Fig. (c), the body is said to be in neutral equilibrium.
Stability of Floating Body
The stability of a floating body is determined form the position of Metacenter (M). In case of floating body, the weight of the body is equal to is the weight of liquid displaced.(a) Stable Equilibrium: If the point M is above G, the floating body will be in stable equilibrium as shown in Fig. (a). If a slight angular displacement is given to the floating body in the clockwise direction, the centre of buoyancy shifts from B to B1 such that the vertical line through B1 cuts at M. Then the buoyant force FB through B1 and weight W through G constitute a couple acting in the anti clockwise direction and thus bringing the floating body in original position.

(b) Unstable E quilibrium: If the point M is below G, the floating body will be in unstable equilibrium as shown in Fig. (b). The disturbing couple is acting in the clockwise direction. The couple due to buoyant force FB and W is also acting in the clockwise direction and thus overturning the floating body.
(c) Neutral Equilibrium: If the point M is at the centre of gravity of the body, the floating body will be in neural equilibrium.
Oscillation (Rolling) of a Floating Body
If a floating body is tilted through an angle by an overturning couple and the over turning couple is suddenly removed then the body will start oscillating. Thus, the body will be in a state of oscillation as if suspended at the metacentre M. This is similar to the case of a pendulum. The only force acting on the body is due to the restoring couple due to the weight W of the body and force of buoyancy FB Time period of oscillation is given by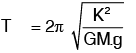
Where
K = Radius of gyration
GM = MetaCentric height
Solved Numericals
Q1: A carton carrying vessel of mass 10 tons (width = length = 5 m, height = 6 m), floats on water. The mass of contents of the vessel are symmetrically placed. If the vessel tilts by 0.01 radians by moving a 50 kg carton from the centre by a distance of 2 m towards side in horizontal direction, the metacentric height of the vessel is (g = 10 m/s2)Ans: Mass of vessel (W) = 10 tonn
= 10 × 103 kg
Mass of carton (w) = 50 kg
b = l = 5 m
h = 6 m
θ = 0.01 rad ≃ tan θ
w × x × cos θ = W × GM × sin θ
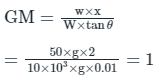
Q2: A body of specific weight w1 floats on a liquid of specific weight w2. Then the ratio of the volume of the object above the liquid to its volume is:
(a) (w2 – w1)/w2
(b) w2/(w2 – w1)
(c) (w2 – w1)/w1
(d) w1/(w2 – w1)
Ans: The specific weight of a body = w1 , Specific weight of a liquid = w2
The body floats on the liquid.
Let assume y% of the part of a body is submerged into the liquid.
Therefore, by the principle of floatation,
Buoyancy force acted by liquid = weight of the body
y × (ρf × g × V) = ρb × g × V
Therefore, y × (w2) = w1 (Part submerged into the liquid)
(Part submerged into the liquid)
Now, the part of a body outside the liquid = 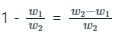
Q3: A piece of metal of specific gravity 7 floats in mercury of specific gravity 13.6. What fraction of its volume is under mercury?
(a) 0.5
(b) 0.4
(c) 0.515
(d) 0.2
Ans: 
From the above formula, the density of metal piece (ρmetal) = 7000 Kg/m3
Similarly, density of fluid i.e. mercury (ρfluid) = 13600 Kg/m3
Applying the equilibrium equation in the vertical direction;
Weight of metal piece (W) = buoyancy force (FB)

|
56 videos|104 docs|75 tests
|
FAQs on Stability of Floating Bodies - Fluid Mechanics for Mechanical Engineering
| 1. What is the concept of buoyancy in relation to stability of floating bodies in mechanical engineering? |  |
| 2. How does the metacentre affect the stability of a submerged body in mechanical engineering? |  |
| 3. What factors contribute to the stability of a floating body in mechanical engineering? |  |
| 4. How does the oscillation (rolling) of a floating body impact its stability in mechanical engineering? |  |
| 5. Can you provide an example of how the stability of a floating body is calculated in mechanical engineering? |  |
|
56 videos|104 docs|75 tests
|

|
Explore Courses for Mechanical Engineering exam
|

|

















