Statics, Rigid Bodies | Basic Physics for IIT JAM PDF Download
Statics is the study of bodies and structures that are in equilibrium. For a body to be in equilibrium, there must be no net force acting on it. In addition, there must be no net torque acting on it. Figure 17A shows a body in equilibrium under the action of equal and opposite forces. Figure 17B shows a body acted on by equal and opposite forces that produce a net torque, tending to start it rotating. It is therefore not in equilibrium.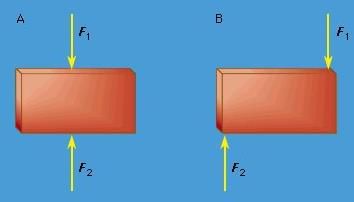
Figure 17: (A) A body in equilibrium under equal and opposite forces. (B) A body not in equilibrium under equal and opposite forces.
When a body has a net force and a net torque acting on it owing to a combination of forces, all the forces acting on the body may be replaced by a single (imaginary) force called the resultant, which acts at a single point on the body, producing the same net force and the same net torque. The body can be brought into equilibrium by applying to it a real force at the same point, equal and opposite to the resultant. This force is called the equilibrant. An example is shown in Figure 18.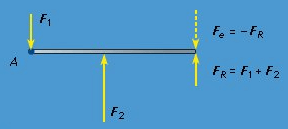
Figure 18: The resultant force (FR) produces the same net force and the same net torque about point A as F1 + F2; the body can be brought into equilibrium by applying the equilibrant force Fe.
The torque on a body due to a given force depends on the reference point chosen, since the torque τ by definition equals r × F, where r is a vector from some chosen reference point to the point of application of the force. Thus, for a body to be at equilibrium, not only must the net force on it be equal to zero but the net torque with respect to any point must also be zero. Fortunately, it is easily shown for a rigid body that, if the net force is zero and the net torque is zero with respect to any one point, then the net torque is also zero with respect to any other point in the frame of reference.
A body is formally regarded as rigid if the distance between any set of two points in it is always constant. In reality no body is perfectly rigid. When equal and opposite forces are applied to a body, it is always deformed slightly. The body’s own tendency to restore the deformation has the effect of applying counterforces to whatever is applying the forces, thus obeying Newton’s third law. Calling a body rigid means that the changes in the dimensions of the body are small enough to be neglected, even though the force produced by the deformation may not be neglected.
Equal and opposite forces acting on a rigid body may act so as to compress the body Figure (19 A) or to stretch it Figure (19 B). The bodies are then said to be under compression or under tension, respectively. Strings, chains, and cables are rigid under tension but may collapse under compression. On the other hand, certain building materials, such as brick and mortar, stone, or concrete, tend to be strong under compression but very weak under tension.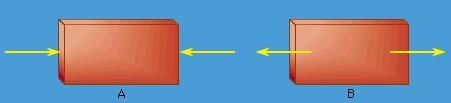
Figure 19: (A) Compression produced by equal and opposite forces. (B) Tension produced by equal and opposite forces.
The most important application of statics is to study the stability of structures, such as edifices and bridges. In these cases, gravity applies a force to each component of the structure as well as to any bodies the structure may need to support. The force of gravity acts on each bit of mass of which each component is made, but for each rigid component it may be thought of as acting at a single point, the centre of gravity, which is in these cases the same as the centre of mass.
To give a simple but important example of the application of statics, consider the two situations shown in Figure 20. In each case, a mass m is supported by two symmetric members, each making an angle θ with respect to the horizontal. In Figure 20A the members are under tension; in Figure 20B they are under compression. In either case, the force acting along each of the members is shown to be
Figure 20: (A) A body supported by two rigid members under tension. (B) A body supported by two rigid members under compression.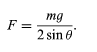 (71)
(71)
The force in either case thus becomes intolerably large if the angle θ is allowed to be very small. In other words, the mass cannot be hung from thin horizontal members only capable of carrying either the compression or the tension forces of the mass.
The ancient Greeks built magnificent stone temples; however, the horizontal stone slabs that constituted the roofs of the temples could not support even their own weight over more than a very small span. For this reason, one characteristic that identifies a Greek temple is the many closely spaced pillars needed to hold up the flat roof. The problem posed by equation 71 was solved by the ancient Romans, who incorporated into their architecture the arch, a structure that supports its weight by compression, corresponding to Figure 20 B.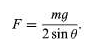 (71)
(71)
A suspension bridge illustrates the use of tension. The weight of the span and any traffic on it is supported by cables, which are placed under tension by the weight. Corresponding to Figure 20 A, the cables are not stretched to be horizontal, but rather they are always hung so as to have substantial curvature.
It should be mentioned in passing that equilibrium under static forces is not sufficient to guarantee the stability of a structure. It must also be stable against perturbations such as the additional forces that might be imposed, for example, by winds or by earthquakes. Analysis of the stability of structures under such perturbations is an important part of the job of an engineer or architect.
|
210 videos|156 docs|94 tests
|
FAQs on Statics, Rigid Bodies - Basic Physics for IIT JAM
| 1. What is statics in physics? |  |
| 2. How are rigid bodies defined in physics? |  |
| 3. What are some examples of rigid bodies? |  |
| 4. How is equilibrium achieved in statics? |  |
| 5. What are the key principles used in statics? |  |

|
Explore Courses for Physics exam
|

|

















