Statistics and Probability (Part - 2) | Quantitative for GMAT PDF Download
Statistics Important Concepts
The Mean
To calculate the mean you sum the values in a data set and divide by the number of values. For example, consider the data set 4, 5 and 9. The sum is 18. The number of values in the set is 3. Therefore, the mean is 18 / 3 = 6.
The Median
The median is the middle number in a data set. Consider the following data set: 4, 2, 7, 5, and 1. You determine the median as follows:
- Order the numbers from the smallest number to the largest number.
- 1, 2, 4, 5, and 7.
- The median is therefore 4.
What happens when the number of values in the set is even? For example, 4, 2, 7 and 5.
- Order the numbers.
- 2, 4, 5 and 7.
- Sum the two middle numbers. 4 + 5 = 9.
- Divide by 2. 9 / 2 = 4.5.
- The median is 4.5.
The Standard Deviation
- The standard deviation is a measure of how far the values in a data set are from the mean. It can be thought of as the average deviation from the mean.
- There is a complicated formula for calculating the standard deviation, but the good news is that we don’t have to use it on the GMAT! However, it is necessary to have a general understanding of what the standard deviation is.
- For example, consider the following dataset: 1, 2 and 3. The mean is 2. Now consider a new data set: 0, 2 and 4. The mean is also 2. However, you can see that in the second set the numbers are more widely spread from the mean. Therefore, the second data set has a larger standard deviation.
The 4 GMAT Probability Rules You Need to Know
Absolutely, probability might seem daunting, but it's not as complex as it appears, especially on the GMAT. Despite the initial intimidation, the probability tested on the GMAT is rooted in fundamental high school math concepts.
The GMAT's quantitative section strictly adheres to high school-level math. Therefore, your grasp of basic probability rules from that level is all that's necessary to excel on this test.
I'll guide you through the four essential probability rules relevant for the GMAT quantitative section in this segment.
#1: Probability Equals the Number of Desired Outcomes Divided by the Number of Possible Outcomes
What does probability really mean? Well, it’s basically a way of figuring out how likely something is to happen.
You can figure out the probability of an event occurring (such as getting heads when you flip a coin) by dividing the number of desired outcomes (in this case, heads), by the number of possible outcomes (in this case, two: heads or tails).
So, the probability of getting heads when you flip a coin is 1/2.
Obviously, not all probability questions will be the simple. But developing a good understanding of what probability actually means will help you figure out the answer to a question. If you’re trying to find the probability of something happening, remember that you first need to figure out how many desired outcomes there are and how many possible outcomes there are.
#2: The Probability of Two Discrete Events Occurring Is the Product of the Two Individual Probabilities
You can find the probability of two discrete events happening by finding the product of the two individual probabilities. What does that mean?
Well, a discrete event is basically an event that occurs which doesn’t have an effect on another event. So, if you flip a coin twice, each coin flip is its own event. They don’t affect each other.
So, to find the probability of two discrete events happening, you need to first find the individual probabilities. We already know that, when you try to get heads while flipping a coin, the probability is 1/2. So, to find the probability of flipping a coin twice and getting two heads is 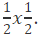

#3: The Probability of Getting One or Another Result Is the Sum of the Two Probabilities
The probability of getting one result or another means that you’re looking for one singular event to happen. So, if you’re looking to find the probability of flipping a coin and getting heads or tails, you will find the sum of the two probabilities.
The probability of flipping a coin and getting heads is 1/2; the probability of flipping a coin and getting tails is 1/2. So, the probability of flipping a coin and getting heads or tails is 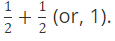
#4: The Probability of Something Not Happening Is One Minus the Probability That It Will Happen
If you’re trying to find the probability of something not happening, first you need to find the probability that it will happen. Sound backwards? Trust me; it’s simple!
If you’re trying to find the probability of flipping a coin and not getting heads, first find the probability of flipping a coin and getting heads. Remember, that probability is 1/2.
Next, subtract that probability from 1.
So, the probability of flipping a coin and not getting heads is 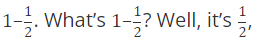 of course! And if you remember, 1/2 is also the probability of flipping a coin and getting tails… or, in other words, the probability of flipping a coin and getting an outcome that’s not heads.
of course! And if you remember, 1/2 is also the probability of flipping a coin and getting tails… or, in other words, the probability of flipping a coin and getting an outcome that’s not heads.
Probability Solved Examples
Example 1: An integer is chosen at random from the first 100 integers. What is the probability that this number will not be divisible by 5 or 8?
Ans: For a number from 1 to 100 not to be divisible by 5 or 8, we need to remove all the numbers that are divisible by 5 or 8.
Thus, we remove 5, 8, 10, 15, 16, 20, 24, 25, 30, 32 35, 40, 45, 48, 50, 55, 56, 60, 64, 65, 70, 72, 75, 80, 85: 88, 90, 95, 96, and 100.
i.e. 30 numbers from the 100 are removed.
Hence, the answer is 70/100 = 7/10 (required probability)
Alternatively, we could have counted the numbers as the number of numbers divisible by 5 + the number of numbers divisible by 8 – the number of numbers divisible by both 5 or 8.
= 20 + 12 – 2 = 30
Example 2: Out of 40 consecutive integers, two are chosen at random. Find the probability that their sum is odd.
Ans: Forty consecutive integers will have 20 odd and 20 even integers. The sum of 2 chosen integers will be odd, only if
First is even and Second is odd OR
First is odd and Second is even
Mathematically, the probability will be given by:
P(First is even) x P(Second is odd) + P(First is odd) x P(second is even)
= (20/40) x (20/39) + (20/40) x (20/39)
= (2 x 202/40 x 39) = 20/39
Example 3: A carton contains 25 bulbs, 8 of which are defective. What is the probability that if a sample of 4 bulbs is chosen, exactly 2 of them will be defective?
Ans: The probability that exactly two balls are defective and exactly two are not defective will be given by
(4C2) x (8/25) x (7/24) x (17/23) x (16/22)
Example 4: The probability that Arjit will solve a problem is 1/5. What is the probability that he solves at least one problem out of ten problems?
Ans: The non-event is defined as:
He solves no problems i.e. he doesn’t solve the first problem and he doesn’t solve the second problem … and he doesn’t solve the tenth problem.
Probability of non-event = (4/5)10
Hence, the probability of the event is 1-(4/5)”
Example 5: Six positive numbers are taken at random and are multiplied together. Then what is the probability that the product ends in an odd digit other than 5?
Ans: The event will occur when all the numbers selected are ending in 1, 3, 7, or 9.
If we take numbers between 1 to 10 (both inclusive), we will have a positive occurrence if each of the six numbers selected is either 1, 3, 7, or 9.
The probability of any number selected being either of these 4 is 4/10 (4 positive events out of 10 possibilities) [Note: If we try to take numbers between 1 to 20, we will have a probability of 8/20 = 4/10. Hence, we can extrapolate up to infinity and say that the probability of any number selected ending in 1, 3, 7, or 9 so as to fulfill the requirement is 4/10.
Hence, answer = (0.4)6
Example 6: The probability that A can solve the problem is 2/3 and B can solve it is 3/4. If both of them attempt the problem, then what is the probability that the problem gets solved.
Ans: The event is defined as:
A solves the problem AND B does not solve the problem
OR
A doesn’t solve the problem AND B solves the problem
OR
A solves the problem AND B solves the problem. Numerically, this is equivalent to:
(2/3) x (1/4) + (1/3) x (3/4) + (2/3) x (3/4)
= (2/12) + (3/12) + (6/12) = 11/12
Example 7: Out of 13 applicants for a job, there are 5 women and 8 men. Two persons are to be selected for the job. The probability that at least one of the selected persons will be a woman is:
Ans: The required probability will be given by
First is a woman and Second is a man OR
First is a man and Second is a woman OR
First is a woman and Second is a woman
i.e. (5/13) x (8/12) + (8/13) x (5/12) + (5/13) x (4/12)
= 100/156 = 25/39
Alternatively, we can define the non-event as: There are two men and no women. Then, the probability of the nonevent is
(8/13) x (7/12) = 56/156
Hence, P(E) = (1– 56/156) = 100/156 = 25/39
[Note: This is a case of probability calculation where repetition is not allowed.]
Example 8: A person has 3 children with at least one boy. Find the probability of having at least 2 boys among the children.
Ans: The event is occurring under the following situations:
- Second is a boy and third is a girl OR
- Second is a girl and third is a boy OR
- Second is a boy and third is a boy
This will be represented by: (1/2) x (1/2) + (1/2) x (1/2) + (1/2) x (1/2) = 3/4
|
121 videos|148 docs|111 tests
|
FAQs on Statistics and Probability (Part - 2) - Quantitative for GMAT
| 1. What is the difference between statistics and probability? |  |
| 2. How are statistics used in real life? |  |
| 3. What is the importance of probability in everyday life? |  |
| 4. How can statistics and probability be applied in data analysis? |  |
| 5. What are the common misconceptions about statistics and probability? |  |
















