Stoichiometry And Gravimetric Analysis - Redox Reactions | Physical Chemistry PDF Download
Stoichiometry
Chemical stoichiometry deals with the determination of quantities of reactants or products of a chemical reaction. The word “stoichiometry” is derived from the Greek word “stoichion “ means element and “ metry “ means measure.
Stoichiometry is divided into two subsections:
(a) Gravimetric analysis
(b) Volumetric analysis Stoichiometry
Stoichiometry
The problems on gravimetric and volumetric analysis can be solved using two well known concepts i.e. mole concept and equivalent concept. But generally, the problems on gravimetric analysis are solved using mole concept since mole concept is easier to apply in such cases while problems on volumetric analysis are solved making use of equivalent concept since it does not require balanced chemical reaction.
However, there is no hard and fast rule that these guidelines should be followed. We can make use of equivalent concept for gravimetric problems and mole concept for volumetric problems.
Let us first understand the mole concept and its use in chemical reactions and then we will learn about equivalent concept:
1. The Mole
The concept of amount of substance is confined to the chemical measurements. The amount of substance of a system is proportional to the number of elementary entities (which may be atoms or molecules or ions or specified group of such particles) of that substance present in the system.
Let us take elements Ag, Mg and Hg with masses equal to their atomic masses in grams, and then to our surprise, each element contains equal number of atoms. This is not only limited to atoms but also applicable to molecules.
For example: If we have molecules like, CO2, NO2, SO2 with masses equal to their molecular masses in grams, then they would also contain equal number of molecules. This specified number of atoms or molecules is referred to as a “mole”.
Thus a system containing a specified number (6.023x1023) of elementary entities is said to contain 1 mole of entities. Thus 1, mole of an iron sample means that the sample contain 6.023 x1023 atoms of iron. Similarly 1 mole of NaCl crystal contains 6.023 x1023 ion pairs (Na+Cl– ).
This specific number 6.023 x1023 elementary entities is called Avogadro’s number or constant (NAV). 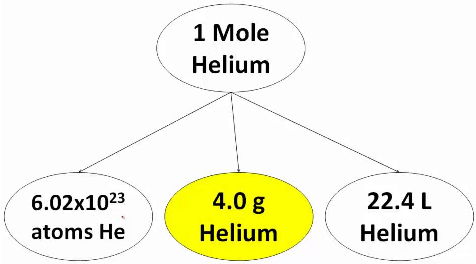 Helium mole
Helium mole
The SI unit for amount of substance is the mole. The mole is defined as the amount of substance in exactly 12g of carbon-12. One mole of any substance contains the same number of elementary entities as there are carbon atoms in exactly 12g of carbon-12.
The mass of specific number (6.023 x1023) of elementary entities is equal to atomic mass for atoms and molecular mass for molecules.
Let M g/mole be molecular mass of a species. Thus M g be the mass of 1 mole (equal to the mass of 6.023x1023 molecules) of the species. Then x g of the species contain mole. Hence
Number of moles of a species =
It is also known that one mole of a gas at STP occupies a volume of 22.4L. Thus, if a gas occupies x L at STP, then the number of moles of the gas can be calculated by dividing the actual volume occupied by the gas at STP with the volume occupied by the gas at STP with the volume occupied by 1 mole of the gas at STP.
Thus, the number of mole of a gas = .
The volume of gas and the number of moles of gas at temperature and pressure other than the STP can be related by ideal gas equation, PV = nRT.
2. Chemical Equations and Stoichiometry
Let the balanced chemical equation we have is
MnO2 + 4HCl → MnCl2 + 2H2O + Cl2
The quantitative information drawn from this balanced chemical equation is:
- The molar ratio in which two reactants (MnO2 and HCl) reacting is 1:4 .
- The molar ratio between the two products can also be known i.e. moles of H2O produced would be double the moles of MnCl2 produced.
- The initial moles of MnO2 and HCl (to be taken in vessel) for the reaction to occur not necessarily be 1 and 4 respectively or in the molar ratio 1:4.
- We can start reaction with MnO2 and HCl taken in any molar ratio, but the moles of two reacting will always be in the molar ratio 1:4.
- The balanced chemical equation should follow the law of conservation of mass.
Let us consider the same chemical system with initial composition as n0MnO2 , n0HCl , n0MnCl2 , n0H2O , n0Cl2 . The n0HCl is four times ofn0MnO2 . When the reaction occurs, these mole numbers change as the reaction progresses. The mole numbers of the various species do not change independently but the changes are related by the stoichiometric coefficients in the chemical equations.
Let after time ‘t’ from the commencement of reaction, the moles of MnO2 reacting be x, then the moles of HCl reacting in the same time interval be 4x since MnO2 and HCl react in the molar ratio of 1: 4.
Thus, after time t, the composition of the system would be:
nMnO2 = n0MnO2 –x
nHCl = n0HCl – 4x
nMnCl2 = n0MnCl2 + x
nH2O = n0H2O + 2x
nCl2 = n0Cl2 + x
The algebraic signs + and – indicates that the reactants are consumed and products are formed.
In general, mole numbers of various species at any time would be given as:
ni = ni0 + vi0x
where ni0 is the initial amount, x is the degree of advancement and vi is the stoichiometric coefficient which will be given a negative sign for the reactants and a positive sign for products .
After long time interval from the commencement of reaction, the composition of the system would be :
nMnO2 = 0 ,nHCl = 0
nMnCl2 = n0MnCl2 + n0MnO2 = = n0MnCl2 + (n0HCl/4)
nH2O = n0H2O + 2n0MnO2 = n0H2O + (n0HCl)/2
nCl2 = n0Cl2 + n0MnO2 = = n0Cl2 + (n0HCl )/4
3. The Limiting Reagent
Let the initial moles of MnO2 and HCl be n0MnO2 and n0HCl respectively and n0HCl ≠ 4 n0MnO2 . thus in the given chemical reaction, after ∞ time , one of the reactant will be completely consumed while the other would be left in excess. Thus, the reactant which is completely consumed when a reaction goes to completion and which decides the yield of the product is called the limiting reagent. 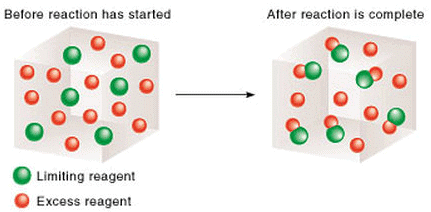 Reaction in presence of limiting reagent
Reaction in presence of limiting reagent
For example: If in the given case n0HCl > 4 n0MnO2, and there is no MnCl2, Cl2 and H2O in the beginning, then
Thus, MnO2 is the limiting reagent and the yield of all the products is governed by the amount of MnO2 taken initially .
Similarly, if in the given case n0HCl < 4 n0MnO2 and no MnCl2 , Cl2 and H2O are present initially, then
Here, HCl would become limiting reagent and the products yield are decided by the amount of HCl taken initially.
The Yield of Product
Let us suppose that the amount of MnCl2 produced in the last case actually be less than n0HCl /4 while theoretical yield should be n0HCl /4. This means that the yield of the product is not 100%. Thus % yield of the product is given as the ratio of actual yield by theoretical maximum yield by 100
% yield of the product =
Gravimetric Analysis
Gravimetric analysis is an analytical technique based on the measurement of mass of solid substances and/or volume of gaseous species.
The gravimetric analysis is broadly classified into three heads:
- Mass-Mass relationship
- Mass- Volume relationship
- Volume - Volume relationship
1. Mass-Mass relationship
This relates the mass of a species (reactant or product) with the mass of another species (reactant or product) involved in a chemical reaction.
Let us consider a chemical reaction,
Let the mass of CaCO3 taken be x g and we want to calculate the mass of CaO obtained by heating x g CaCO3. Then the moles of CaCO3 taken would be x/M1 (where M1 represents the molar mass of CaCO3). According to the balanced reaction, the molar ratio of CaCO3 and CaO is 1: 1, so same number of moles (x/M1) of CaO would be formed.
Now for converting the moles of CaO into mass of CaO obtained, we need to multiply the moles of CaO with molar mass of CaO. Let the molar mass of CaO be M2, so the mass of CaO obtained by heating x g of CaCO3 would be
2. Mass- Volume relationship
This establishes the relationship between the mass of a species (reactant or product ) and the volume of a gaseous species ( reactant or product ) involved in a chemical reaction. Let us take x g of CaCO3 in a vessel of capacity V L and the vessel is heated so that CaCO3 decomposes as
We want to find out the volume of CO2 evolved at STP by heating x g of CaCO3. Then
Moles of CaCO3 = x/M1
Moles Of CO2 evolved = x/M1 (since molar ratio of CaCO3 and CO2 is 1:1 )
Volume Of CO2 evolved at STP =
But, if the volume of CO2 evolved is to be calculated at pressure P atm and temperature T K.
Then, moles of CO2 evolved =
Volume of CO2 evolved at pressure P and temperature
3. Volume - Volume relationship
This relationship deals with the volume of a gaseous species (reactant or product ) with the volume of another gaseous species ( reactant or product )involved in a chemical reaction .
Let us consider the reaction N2 (g) + 3H2 (g) → 2NH3 (g) . We are given x L of N2 at pressure P atm and temperature T K and we want to know the volume of H2 required to react with it at the same pressure and temperature.
Moles of N2 =
Moles of H2 required = (since molar ratio of N2 and H2 is 1:3 )
Volume of H2 required at same temperature and pressure =
This result could also have been obtained by knowing that for a gaseous relation, at the same pressure and temperature, the moles of gas is directly proportional to volume of the gas (V α n since P and T are constant) or molar ratio and volume ratio are the same.
Thus, when x L of N2 is taken at pressure P atm and temperature T , then at the same pressure and temperature, the volume of H2 required would be 3xL ( since the volume ratio of N2 and H2 would be same as molar ratio i.e. 1:3). But if the volume of H2 required is to be calculated at another pressure P’ atm and temperature T’ K. then
Moles of H2 required =
Volume of H2 required at P’ atm and temperature T’ K
|
90 videos|144 docs|67 tests
|
FAQs on Stoichiometry And Gravimetric Analysis - Redox Reactions - Physical Chemistry
| 1. What is stoichiometry? |  |
| 2. How is stoichiometry useful in gravimetric analysis? |  |
| 3. What are redox reactions? |  |
| 4. How does stoichiometry relate to redox reactions? |  |
| 5. Can stoichiometry be applied to other areas of chemistry besides gravimetric analysis? |  |






















