Strictly Binary Tree | Programming and Data Structures - Computer Science Engineering (CSE) PDF Download
Introduction
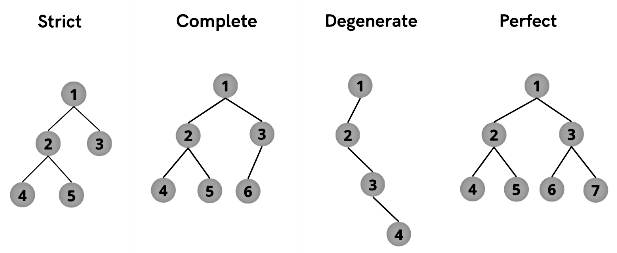
A Strict Binary Tree is also known as Proper Binary Tree and Full Binary Tree. A Binary Tree is identified as a Strict Binary Tree if each parent node contains either no or two children. All nodes contain two children in a Strict Binary Tree except the leaf nodes which have 0 children.

The above figure is an example of a Strict Binary Tree. The internal nodes (node 1, node 2, node 3, node 5) have 2 children each, whereas the leaf nodes (node 4, node 6, node 7, node 8, node 9) have no children.
Properties
- i = number of internal nodes
- l = number of leaf nodes
- n = total number of nodes
- h = height of the tree
- The number of leaf nodes in a Strict Binary Tree will be one greater than the internal nodes. In the above example, there are 4 internal nodes and 5 leaf nodes.
- This can be represented as l = i + 1
- The total number of nodes in terms of internal nodes can be calculated as n = 2i + 1 and in terms of leaf nodes, n = 2l - 1. Conversely, the number of internal nodes, i = (n - 1) / 2 and number of leaf nodes, l = (n + 1) / 2.
- The maximum number of nodes is the same as the number of nodes in the binary tree, 2^(h+1) – 1.
- The minimum number of nodes in a tree of height h is 2^h + 1
- The minimum possible height or the minimum number of levels is ***log2(n+1)***.
Program
To check whether a given Binary Tree is a Strict Binary Tree, we need to find out the number of children a node has. If any node in the tree has 1 child, the tree will not be qualified as a Strict Binary Tree.
Steps:
- Construct a Binary Tree.
- Traverse through the tree in Depth-First-Search (DFS) manner.
- Check if the node has 0 children. If yes, return true.
- Check if the node has 2 children. If yes, check the validity of both the children and return the answer.
- If neither of the cases is true, the node contains 1 child. Return false in this case since the tree is not a Strict Binary Tree.
Pseudocode
FUNCTION isStrictTree(node)
IF right and left child are null
RETURN true
IF right and left child both are not null
CALL isStrictTree(left child) && isStrictTree(right child)
ELSE
RETURN false
Java Implementation:
// define the nodes of the binary tree
class Node {
int val;
Node left;
Node right;
// constructor for Node class
Node(int num) {
val = num;
left = right = null;
}
}
// Binary tree construction and operations
class BinaryTree {
Node root;
// function to check if a tree is a strict binary tree
boolean isStrictTree(Node node) {
// in case the tree is empty, it is a strict binary tree
if (node == null)
return true;
// in case the node is a leaf node and has no children
if (node.left == null && node.right == null)
return true;
// if both left and right subtrees are not null and the node has two children
if ((node.left != null) && (node.right != null))
return isStrictTree(node.left) && isStrictTree(node.right);
// the last case where the node has one child
return false;
}
// function to print whether a tree is strict binary or not
void printResult(Node node) {
if (isStrictTree(node))
System.out.println("The binary tree is a Strict Binary Tree");
else
System.out.println("The binary tree is not a Strict Binary Tree");
}
public static void main(String args[]) {
// construct the binary tree for case A
BinaryTree casea = new BinaryTree();
casea.root = new Node(1);
casea.root.left = new Node(2);
casea.root.right = new Node(3);
casea.root.left.left = new Node(4);
casea.root.left.right = new Node(5);
casea.root.right.left = new Node(6);
casea.root.right.right = new Node(7);
casea.root.left.left.left = new Node(8);
casea.root.left.left.right = new Node(9);
// print result for case A
casea.printResult(casea.root);
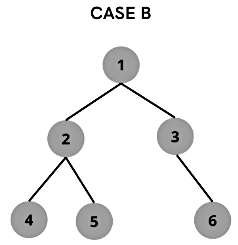
// construct the binary tree for case B
BinaryTree caseb = new BinaryTree();
caseb.root = new Node(1);
caseb.root.left = new Node(2);
caseb.root.right = new Node(3);
caseb.root.left.left = new Node(4);
caseb.root.left.right = new Node(5);
caseb.root.right.right = new Node(6);
// print result for case B
caseb.printResult(caseb.root);
}
}

Output
The binary tree is a Strict Binary Tree
The binary tree is not a Strict Binary Tree
Time complexity: O(N) where n is number of nodes in given binary tree.
Auxiliary Space: O(N) for call stack since using recursion
Comparison
Types of Binary Tree
1. Complete Binary Tree
A Binary tree is identified as a Complete Binary tree if all the nodes are added from the left, so nodes are not added to a new level until the previous level is completely filled. In the last level, all the nodes must be as left as possible.
- Internal nodes can have 0, 1 or 2 children. However, the nodes have to be added from the left so only one internal node can have one child, others will have 0 or 2 children.
- Leaf nodes are at the last level.
- The maximum number of nodes in a complete binary tree of height h is 2^(h+1) - 1 and minimum number of nodes are 2^h.
2. Perfect Binary Tree
A Binary tree is a Perfect Binary Tree if all the internal nodes have 2 children and the levels are completely filled, including the last level. The leaf nodes are present at the same level which forms the last level of the tree. All Perfect Binary trees are Strict Binary Tree.
- All the internal nodes have 2 children.
- Leaf nodes are at the same level.
- A perfect binary tree of height h has 2^(h + 1) – 1 node and 2^h leaf nodes.
3. Degenerate Binary Tree
A degenerate or pathological tree is a binary tree having a single child. It could be a left or right child. A degenerate tree where the nodes only have the right child is called a right skewed binary tree whereas a tree where the nodes have left child only is called a left skewed binary tree.
- All the internal nodes have only one child.
- There is only one leaf node which is present at the last level.
- A Degenerate Binary Tree of height h will have h + 1 nodes.
|
119 docs|30 tests
|

|
Explore Courses for Computer Science Engineering (CSE) exam
|

|
















