Study Notes for Resonance | Theory of Machines (TOM) - Mechanical Engineering PDF Download

Resonance

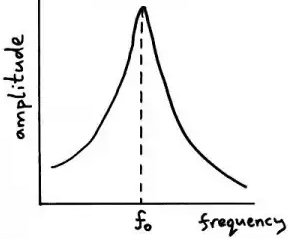
• When the frequency of external force(driving frequency) is equal to the natural frequency of a vibrating body, the amplitude of vibration becomes excessively large. This phenomenon is known as resonance.
• If an object is being forced to vibrate at its natural frequency, resonance will occur and you will observe large amplitude vibrations. The resonant frequency is f_o.
  

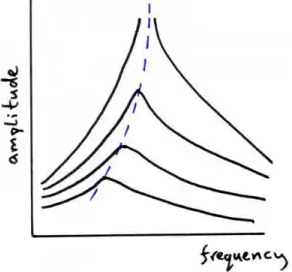
Effect of Damping on Resonance Graph

The amplitude of the resonance peak decreases and the peak occurs at a lower frequency.

Phase and Resonance

1. The phase relationship between the driving oscillation and the oscillation of the object being driven is different at different frequencies.
   (i) Below resonance,e they are in phase with each other.
   (ii) At resonance, the phase relationship is 90º or π/2 rad.
   (iii) Above resonance, the phase relationship is 180º or π rad.
2. All structures have a resonant frequency.
3. If you impact the structure with enough force to make it move, it will vibrate briefly at its natural frequency.
4. A structure will have a resonant frequency in each of its 3 directional planes (x, y and z, or as we call them, horizontal, vertical and axial).
5. Resonance serves to amplify the vibration due to whatever vibration force is present at (or near) that resonant frequency.
6. It is important to note that resonance does not cause vibration, it amplifies it.
7. Resonance problems occur in two primary forms. They are:

Critical speeds

• It occurs when a component rotates at its own natural frequency.
  (i) A "critical speed" is simply when the rotational speed (rpm) coincides with the natural frequency of the rotor (cpm).
  (ii) The tiniest amount of residual unbalance (something that is always present) is enough to cause huge amounts of vibration when rotating at a critical.
  (iii) Rotors that are sped up or slowed down slowly are susceptible to this (i.e. turbines). In these cases, the critical speed is usually well known.

Structural resonances 

1. This is far more common than a critical speed problem. It becomes a problem when some forcing frequency comes close (+/- 10%) to the resonant (natural) frequency of a structure.
   (i) The structure can be the machine housing itself or some nearby structure such as a hand rail or I-beam.
   (ii) The structure itself will vibrate excessively - do not confuse with a critical speed.
   (iii) The "shape" of the structure's vibration is an important clue and is known as a "mode shape".
   (iv) Testing for the structure's natural frequency is crucial (required) to confirming a resonance problem.
2. Resonance, once diagnosed, can be simple to correct. It can also be extremely complex and difficult to correct.
3. One method for determining a critical speed is a "Coast Down/Start Up Plot".
4. This plot consists of the 1x vibration amplitude being collected simultaneously with a 1x rpm phase reading as the machine coasts to a stop or goes from stopped to full running speed.
5. This test requires a 1x rpm reference (from a photoeye or some other speed tracking signal) in order to track the amplitude and phase at that frequency.
6. Two things are observed as the rotor passes through a critical:
   (i) The 1x rpm amplitude will increase until the rotor reaches it's critical and then decrease to the normal level as the speed continues to change.
   (ii) Phase will shift 180° as the rotor passes through the critical. This is due to the rotor changing from a rigid rotor (while operating below it's critical) to a flexible rotor (while operating above it's critical
7. If the measured response of the structure (i.e. it's resonant frequency) is within about 10% of the forcing frequency (i.e. the rpm of the machine although it can be at any frequency), resonance should be considered a problem. The closer the two frequencies are, the more of a problem it is.

To correct a resonance problem, there are 4 methods:

1. Stiffen the structure: This method raises the resonant frequency of the structure.
2. Add mass to the structure: This method lowers the resonant frequency.
3. Change exciting frequency: Change the speed of the machine.
4. Add a dynamic absorber to the structure: This method attaches the equivalent of a tuning fork to the structure. This attachment is tuned to have the same resonant frequency as the structure and sets up an out-of-phase signal that has the effect of cancelling out (reducing) the signal being generated by the structure. The dynamic absorber must be properly sized to handle the forces being generated.