Subgraphs & Induced Subgraphs | Engineering Mathematics - Engineering Mathematics PDF Download
Introduction
In this tutorial, we’ll explain what an induced subgraph is. We’ll also show how to construct it, how to check if a (sub)graph is induced, and how to find the induced graph isomorphism.
Subgraphs
Let’s say we have a graph G=(V, E), where V is the set of nodes, and E denotes the edges between them. A subgraph of G is any graph G'=(V', E') such that V' ⊂ V and E' ⊂ E. In other words, each node in a subgraph is also a node in the supergraph. Further, every edge in the subgraph is an edge in the supergraph.
For example, all these graphs:
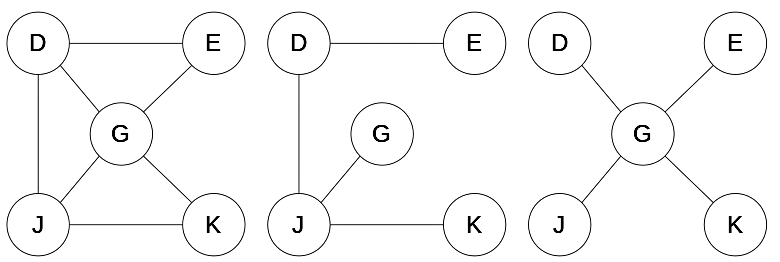
Can be listed as subgraphs of:
Induced Subgraphs
An induced subgraph is a special case of a subgraph. If S is a subset of G‘s nodes, then the subgraph of G induced by S is the graph that has S as its set of vertices and contains all the edges of G that have both endpoints in S. This definition covers both directed and undirected graphs. Also, it covers the weighted just as the unweighted ones.
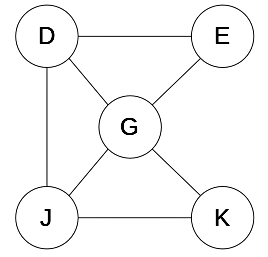
Given G and S, the induced subgraph is unique. There’s only one subgraph induced by {D, E, G, J, K} in the above graph:
What’s the Difference?
- The concepts of an induced subgraph and an ordinary subgraph are very similar. The difference is that an induced subgraph includes all the edges that have both endpoints in the inducing set S, whereas an ordinary subgraph may miss some.
- So, an induced subgraph keeps both adjacency and non-adjacency of the inducing vertices, in contrast to an ordinary subgraph that preserves only non-adjacency.
Induced Subgraph Problems and Algorithms
Let’s introduce a few problems related to induced subgraphs.
1. Induced Subgraph Construction
Here, the input consists of the graph G=(V, E) and the inducing set S⊆ V. Our goal is to construct the induced subgraph Gs = (S, ES). We’ll do so by iterating over the edges in E and keeping only those whose both endpoints are in S:

The time complexity depends on how we represent the graphs. Using linked lists, we traverse each edge incident to a node in S twice, so the time complexity is \Theta(|E_S|). On the other hand, if we use matrices, we traverse the whole row of |V| entries for each of the |S| inducing nodes. Therefore, the complexity will be \Theta(|S|\cdot |V|).
2. How to Check if a Subgraph Is Induced
In this problem, we have a graph G1 = (V1,E1) and its subgraph G2 = (V2,E2) (so V2 ⊂ V1 and E2 ⊂ E1) Our goal is to check if G2 is an induced subgraph of G1. To do so, we iterate over the edges incident to V2 in G1. If we find an edge that isn’t in E2, we can conclude that G2 isn’t an induced subgraph because it doesn’t preserve adjacency. Otherwise, we conclude that G2 is induced:

As before, the complexity depends on the way we represent the graphs.
We don’t need to check if G2 contains an edge not in G1. That’s because of the way we defined the input. Since we know that G2 is a subgraph of G1, E2 can’t contain an edge that’s not in E1.
3. How to Check if a Graph Is an Induced Subgraph
However, if we get G_2 as a graph of some nodes in V_1, we’ll have to check both that G_2 is a subgraph and that it is induced.

4. Induced Subgraph Isomorphism
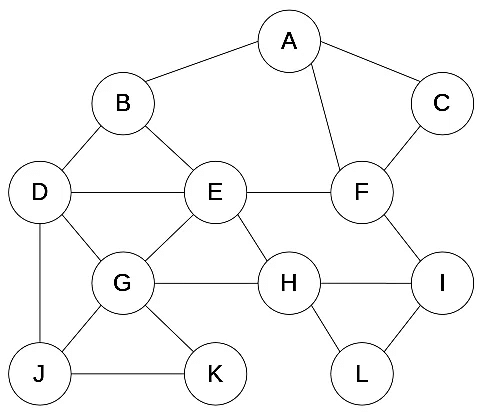
The Induced Subgraph Isomorphism (ISI) is an injective mapping from one graph G2 = (V2, E2) to an induced subgraph of another, G1 = (V1, E1) . So, we get G1 and G2 at the input and find an ISI mapping from the former to the latter.
Unlike in the previous two problems, G2 and G1 don’t use the same labels for their nodes. So, we have to find a mapping that translates G2 to an induced subgraph of G1:
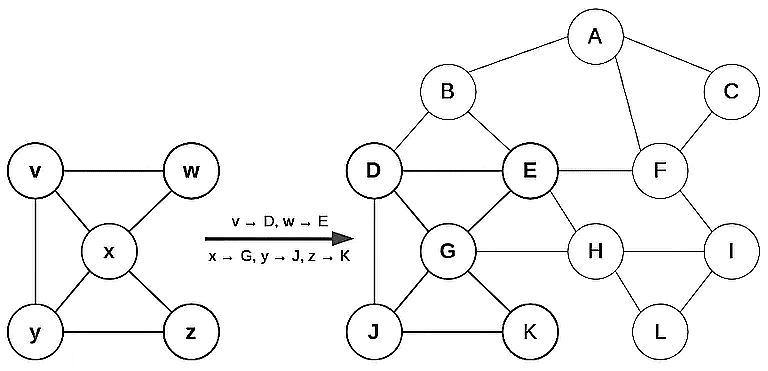
Formally, we say that f: V2 → V1 is an ISI if and only if it satisfies: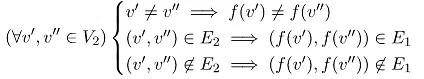 The first condition states that f is an injective function. The second is that an ISI preserves adjacency, and the third is that it also keeps non-adjacency.
The first condition states that f is an injective function. The second is that an ISI preserves adjacency, and the third is that it also keeps non-adjacency.
This problem is NP-hard, which means that no polynomial-time algorithm for solving it is known to date. We can treat it as a constraint-satisfaction problem (CSP) and solve it like we solve other CSPs. The Equation (1) lists all the constraints we need to define the CSP and feed it to the universal solver. Each f(v) for v ∈ V2 will correspond to a CSP variable, and each variable will have the whole set V1 as its domain.
Subgraphs
A subgraph S of a graph G is a graph whose set of vertices and set of edges are all subsets of G. (Since every set is a subset of itself, every graph is a subgraph of itself.)
All the edges and vertices of G might not be present in S; but if a vertex is present in S, it has a corresponding vertex in G and any edge that connects two vertices in S will also connect the corresponding vertices in G. All of these graphs are subgraphs of the first graph.
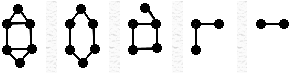
A vertex-induced subgraph is one that consists of some of the vertices of the original graph and all of the edges that connect them in the original. An edge-induced subgraph consists of some of the edges of the original graph and the vertices that are at their endpoints.
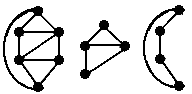
The second two figures are vertex-induced subgraphs of the first figure.
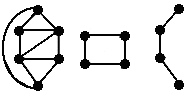
The second two figures are edge-induced subgraphs of the first figure.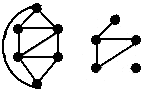
The second figure is a subgraph of the first figure, but it is neither edge-induced nor vertex-induced.
A spanning subgraph is a subgraph that contains all the vertices of the original graph. A spanning tree is a spanning subgraph that is often of interest. A cycle in a graph that contains all the vertices of the graph would be called a spanning cycle. However it's more common name is a Hamiltonian cycle.
Conclusion
In this article, we talked about induced and ordinary subgraphs. We also presented a few common problems related to the former subgraphs. Those are the induced subgraph construction, verification, and isomorphism.
|
65 videos|129 docs|94 tests
|
















