Subset Sum Problem | Algorithms - Computer Science Engineering (CSE) PDF Download

Introduction

Given a set of non-negative integers, and a value sum, determine if there is a subset of the given set with sum equal to given sum.
Example:

1. Input: set[] = {3, 34, 4, 12, 5, 2}, sum = 9
   Output: True  
   There is a subset (4, 5) with sum 9.
2. Input: set[] = {3, 34, 4, 12, 5, 2}, sum = 30
   Output: False
   There is no subset that add up to 30.

Methods

1. Method 1: Recursion.
Approach: For the recursive approach we will consider two cases.

• Consider the last element and now the required sum = target sum – value of ‘last’ element and number of elements = total elements – 1
• Leave the ‘last’ element and now the required sum = target sum and number of elements = total elements – 1

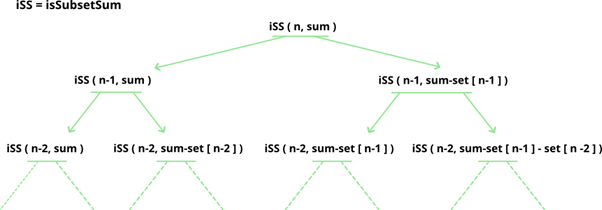
Following is the recursive formula for isSubsetSum() problem:
isSubsetSum(set, n, sum)
= isSubsetSum(set, n-1, sum) ||  
  isSubsetSum(set, n-1, sum-set[n-1])
Base Cases:
isSubsetSum(set, n, sum) = false, if sum > 0 and n == 0
isSubsetSum(set, n, sum) = true, if sum == 0
Let’s take a look at the simulation of above approach:
set[] = {3, 4, 5, 2}
sum = 9
(x, y) = 'x' is the left number of elements,
'y' is the required sum

• C++
  
• Java
  
• Python3
  
• C#
  
• PHP
  
• Javascript
  

Output: Found a subset with given sum
Complexity Analysis: The above solution may try all subsets of given set in worst case. Therefore time complexity of the above solution is exponential. The problem is in-fact NP-Complete (There is no known polynomial time solution for this problem).

2. Method 2: To solve the problem in Pseudo-polynomial time use the Dynamic programming.
So we will create a 2D array of size (arr.size() + 1) * (target + 1) of type boolean. The state DP[i][j] will be true if there exists a subset of elements from A[0….i] with sum value = ‘j’.
The approach for the problem is:
if (A[i-1] > j)
DP[i][j] = DP[i-1][j]
else
DP[i][j] = DP[i-1][j] OR DP[i-1][j-A[i-1]]

• This means that if current element has value greater than ‘current sum value’ we will copy the answer for previous cases
• And if the current sum value is greater than the ‘ith’ element we will see if any of previous states have already experienced the sum=’j’ OR any previous states experienced a value ‘j – A[i]’ which will solve our purpose.

The below simulation will clarify the above approach:

Below is the implementation of the above approach:

• C++
  

  
  

• Java
  
  
• Python3
  
  
• C#
  
  
• PHP
  
  
• Javascript
  
  

Output: Found a subset with given sum

Memoization Technique for finding Subset Sum

Method:

1. In this method, we also follow the recursive approach but In this method, we use another 2-D matrix in  we first initialize with -1 or any negative value.
2. In this method, we avoid the few of the recursive call which is repeated itself that’s why we use 2-D matrix. In this matrix we store the value of the previous call value.

Below is the implementation of the above approach:

• C++
  
  

Output: YES
Complexity Analysis 

• Time Complexity: O(sum * n), where sum is the ‘target sum’ and ‘n’ is the size of array.
• Auxiliary Space: O(sum * n), as the size of 2-D array is sum * n.