Substitution method of Integration, Business Mathematics & Statistics | Business Mathematics and Statistics - B Com PDF Download
Integration by Substitution
"Integration by Substitution" (also called "u-substitution") is a method to find an integral, but only when it can be set up in a special way.
The first and most vital step is to be able to write our integral in this form:
Note that we have g(x) and its derivative g'(x)
Like in this example:
Here f=cos, and we have g=x2 and its derivative of 2x
This integral is good to go!
When our integral is set up like that, we can do this substitution:
Then we can integrate f(u), and finish by putting g(x) back as u.
Like this:
Example: 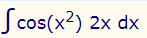
We know (from above) that it is in the right form to do the substitution:
Now integrate:
|
And finally put u=x2 back again:
sin(x2) + C
worked out really nicely! (Well, I knew it would.)
This method only works on some integrals of course, and it may need rearranging:
Example:
Oh no! It is 6x, not 2x. Our perfect setup is gone.
Never fear! Just rearrange the integral like this:
(We can pull constant multipliers outside the integration, see Rules of Integration.)
Then go ahead as before:
Now put u=x2 back again:
3 sin(x2) + C
Done!
Now we are ready for a slightly harder example:
Example:
Let me see ... the derivative of x2+1 is 2x ... so how about we rearrange it like this:
Then we have:
Then integrate:
Now put u=x2+1 back again:
½ ln(x2+1) + C
And how about this one:
Example:
Let me see ... the derivative of x+1 is ... well it is simply 1.
So we can have this:
Then we have:
Then integrate:
Now put u=x+1 back again:
In Summary
- When we can put an integral in this form:
- Then we can make u=g(x) and integrate ∫f(u) du
- And finish up by re-inserting g(x) where u is.
|
124 videos|176 docs
|
FAQs on Substitution method of Integration, Business Mathematics & Statistics - Business Mathematics and Statistics - B Com
| 1. What is the substitution method of integration? |  |
| 2. How does the substitution method work in integration? |  |
| 3. When should I use the substitution method in integration? |  |
| 4. What are the steps involved in using the substitution method of integration? |  |
| 5. Can you provide an example of using the substitution method in integration? |  |
















