Sum of the Measures of the Exterior Angles of a Polygon | Mathematics (Maths) Class 8 PDF Download
Polygon is a closed, connected shape made of straight lines. It may be a flat or a plane figure spanned across two-dimensions. A polygon is an enclosed figure that can have more than 3 sides. The lines forming the polygon are known as the edges or sides and the points where they meet are known as vertices. The sides that share a common vertex among them are known as adjacent sides. The angle enclosed within the adjacent side is called the interior angle and the outer angle is called the exterior angle.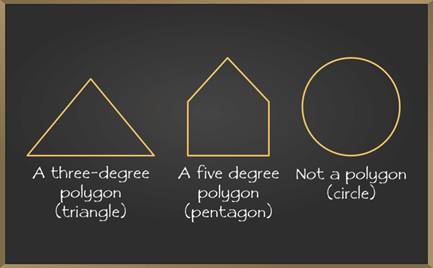
Exterior Angle
An exterior angle basically is formed by the intersection of any of the sides of a polygon and extension of the adjacent side of the chosen side. Interior and exterior angles formed within a pair of adjacent sides form a complete 180 degrees angle.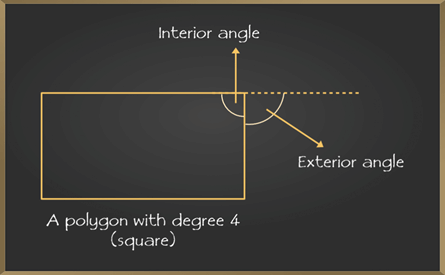
Measures of Exterior Angles
- They are formed on the outer part, that is, the exterior of the angle.
- The corresponding sum of the exterior and interior angle formed on the same side = 180°.
- The sum of all the exterior angles of the polygon is independent of the number of sides and is equal to 360 degrees, because it takes one complete turn to cover polygon in either clockwise or anti-clockwise direction.
- If we have a regular polygon of n sides, the measure of each exterior angle
= (Sum of all exterior angles of polygon)/n
= (360 degree)/n
Theorem for Exterior Angles Sum of a Polygon
If we observe a convex polygon, then the sum of the exterior angle present at each vertex will be 360°. Following Theorem will explain the exterior angle sum of a polygon:
Proof
Let us consider a polygon which has n number of sides. The sum of the exterior angles is N.
The sum of exterior angles of a polygon(N) =
Difference between {the sum of the linear pairs (180n)} – {the sum of the interior angles
(180(n – 2))}
N = 180n − 180(n – 2)
N = 180n − 180n + 360
N = 360
Hence, we have the sum of the exterior angle of a polygon is 360°.
Sample Problems on Exterior Angles
Example 1: Find the exterior angle marked with x. 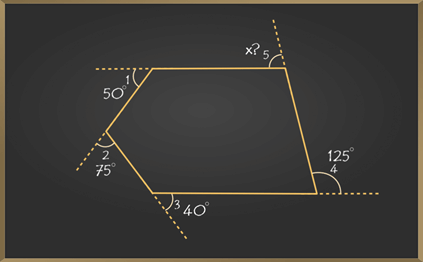
Solution:
Since the sum of exterior angles is 360 degrees, the following properties hold:
∠1 + ∠2 + ∠3 + ∠4 + ∠5 = 360°
50° + 75° + 40° + 125° + x = 360°
x = 360°
Example 2: Determine each exterior angle of the quadrilateral.
Solution: Since, it is a regular polygon, measure of each exterior angle
= 360°
Number of sides
= 360°
4
= 90°
Example 3: Find the regular polygon where each of the exterior angle is equivalent to 60 degrees.
Solution: Since it is a regular polygon, the number of sides can be calculated by the sum of all exterior angles, which is 360 degrees divided by the measure of each exterior angle.
Number of sides = Sum of all exterior angles of a polygon
n
Value of one pair of side = 360 degree
60 degree
= 6
Therefore, this is a polygon enclosed within 6 sides, that is hexagon.
Example 4: Find the interior angles ‘x, y’, and exterior angles ‘w, z’ of this polygon? 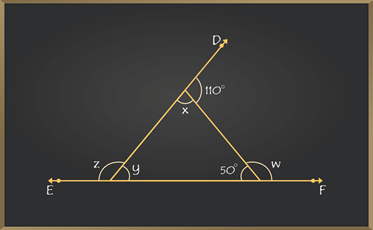
Solution:
Here we have ∠DAC = 110° that is an exterior angle and ∠ACB = 50° that is an interior angle.
Firstly we have to find interior angles ‘x’ and ‘y’.
∠DAC + ∠x = 180° {Linear pairs}
110° + ∠x = 180°
∠x = 180° – 110°
∠x = 70°
Now,
∠x + ∠y + ∠ACB = 180° {Angle sum property of a triangle}
70°+ ∠y + 50° = 180°
∠y + 120° = 180°
∠y = 180° – 120°
∠y = 60°
Secondly now we can find exterior angles ‘w’ and ‘z’.
∠w + ∠ACB = 180° {Linear pairs}
∠w + 50° = 180°
∠w = 180° – 50°
∠w = 130°
Now we can use the theorem exterior angles sum of a polygon,
∠w + ∠z + ∠DAC = 360° {Sum of exterior angle of a polygon is 360°}
130° + ∠z + 110° = 360°
240° + ∠z = 360°
∠z = 360° – 240°
∠z = 120°
|
79 videos|408 docs|31 tests
|
FAQs on Sum of the Measures of the Exterior Angles of a Polygon - Mathematics (Maths) Class 8
| 1. What is the formula for calculating the sum of the measures of the exterior angles of a polygon? |  |
| 2. How can I find the measure of each exterior angle of a regular polygon? |  |
| 3. Can the sum of the measures of the exterior angles of a polygon be greater than 360 degrees? |  |
| 4. Are the exterior angles of a polygon always congruent? |  |
| 5. How does the number of sides in a polygon affect the sum of the measures of its exterior angles? |  |

|
Explore Courses for Class 8 exam
|

|

















