Summation of Series | Mathematics (Maths) Class 11 - Commerce PDF Download
G. Summation of series



Remarks :
(i) r =
r =  (sum of the first n natural nos.)
(sum of the first n natural nos.)
(ii) r² =
r² =  (sum of the squares of the first n natural numbers)
(sum of the squares of the first n natural numbers)
(iii) r3 =
r3 = 
 (sum of the cubes of the first n natural numbers)
(sum of the cubes of the first n natural numbers)
(iv) r4 =  (n + 1) (2n + 1) (3n² + 3n - 1)
(n + 1) (2n + 1) (3n² + 3n - 1)
Method Of Differences :
Let u1, u2, u3...... be a sequence, such that u2 - u1, u3 - u2,............. is either an A.P. or a G.P. then nth term un of this sequence is obtained as follows
S = u1 + u2 + u3 + ....... + un ...(i)
S = u1 + u2 + .......... + un - 1 + un ...(ii)
(i) - (ii) ⇒un = u1 + (u2 - u1) + (u3 - u2) + ........... + (un - un - 1)
Where the series (u2 - u1) + (u3 - u2) + ......... + (un - un - 1) is
either in A.P. or in G.P. then we can find un and hence sum of this series as S = 
Remark : It is not always necessary that the series of first order of differences i.e. u2-u1, u3-u2 ... un-un - 1
is always either in A.P. or in G.P. in such case let u1 = T1, u2 - u1 = T2, u3 - u2 = T3 .......,un - un - 1 = Tn.
So un = T1 + T2 + ....... + Tn .... (i)
un = T1 + T2 + ........ + Tn -1 + Tn .... (ii)
(i) - (ii) ⇒ Tn = T1 + (T2 - T1) + (T3 - T2) + ...... + (Tn + Tn - 1)
Now, the series (T2 - T1) + (T3 - T2) + ..... + (Tn - Tn - 1) is series of second order of differences and when it is either in A.P. or in G.P., then un = 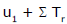
Otherwise in the similar way we find series of higher order of differences and the nth term of the series.
If possible express rth term as difference of two terms as tr = f(r) - f(r ± 1) . This can be explained with help of examples given below.
Ex.35 Find the sum to n terms of the series,
0.7 + 7.7 + 0.77 + 77.7 + 0.777 + 777.7 + 0.7777 + ...... where n is even .
Sol. n = 2m
s = (0.7 + 0.77 + 0.777 + ...... m term) + (7.7 + 77.7 + 777.7 + ...... m terms)
= (0.9 + 0.99 + 0.999 + ..... m terms) +
(0.9 + 0.99 + 0.999 + ..... m terms) +  ((102 - 1) + (103 - 1) + ..... + (10m + 1 - 1))
((102 - 1) + (103 - 1) + ..... + (10m + 1 - 1))
= 
 +
+ 

Ex.36 Determine the sums of the following series
1. 1 +  ;
;
2. 1 -  .
.
Sol. To determine the required sums first compute the following sum



For computing the first of the sums put in the deduced formula x =  . then we have
. then we have
1 +  +
+  +
+  + .... +
+ .... +  {3(2n - 1) - 2n}
{3(2n - 1) - 2n}
And putting x = –1/2, we find


Ex.37 There are n necklaces such that the first necklace contains 5 beads, the second contains 7 beads and, in general the ith necklace contains i beads more than the number of beads in (i- 1)th necklace. Find the total number of beads is all the n necklaces.
Sol. Let us write the sequence of the number of beads in the 1st, 2nd, 3rd, ...., nth necklaces.
= 5, 7, 10, 14, 19, ........ = (4 + 1), (4 + 3), (4 + 6) (4 + 10), (4 + 15),. ......, 
Sn = Total number of beads in the n necklaces
Sn =  + 1 + 3 + 6 + .... +
+ 1 + 3 + 6 + .... + 
= 4n + Sum of the first n triangular numbers =
= 4n + 
= 4n + 
=  [48n + 2n(n + 1) (n + 2)]
[48n + 2n(n + 1) (n + 2)]
=  [n2 + 3n + 26].
[n2 + 3n + 26].
Ex.38 If S1, S2, S3, ... Sn, .... are the sums of infinite geometric series whose first terms are 1, 2, 3, ... n, ... and whose common ratios are , , , ...., , ... respectively, then find the value of
, ... respectively, then find the value of  .
.
Sol. rth series will have a = r and common ratio is 
∴ Sr =  =
=  = r + 1
= r + 1
∴  = (r + 1)2
= (r + 1)2
∴  =
= 
= 22 + 32 + 42 + ....... +(2n - 1)2 + (2n)2 = 12 + 22 + 32 + ..... + (2n)2 - 1
= sum of the square of the first (2n) natural numbers = -1
-1
= 
Ex.39 Find the sum to n-terms 3 + 7 + 13 + 21 + ......
Sol. Let S = 3 + 7 + 13 + 21 + ............. + Tn ................(i)
S = 3 + 7 + 13 + ................+ Tn - 1 + Tn ...............(ii)
(i) - (ii) ⇒ Tn = 3 + 4 + 6 + 8 + ..................... + (Tn - Tn - 1)
= 3 +  [8 + (n - 2)2] = 3 + (n - 1) (n + 2) = n2 + n + 1
[8 + (n - 2)2] = 3 + (n - 1) (n + 2) = n2 + n + 1
Hence S = S(n2 + n + 1) = S n2 + S n + S 1 =  + n =
+ n =  (n2 + 3n + 5)
(n2 + 3n + 5)
Ex.40 Find the sum of n-terms 1 + 4 + 10 + 22 + .......
Sol. Let S = 1 + 4 + 10 + 22 + ...... + Tn .... (i)
S = 1 + 4 + 10 + ........+Tn - 1 + Tn .... (ii)
(i) - (ii)
⇒ Tn = 1 + (3 + 6 + 12 + ...... + Tn - Tn - 1)
= 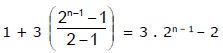
So S = 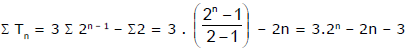
Ex.41 Find the nth term and the sum of n term of the series 2, 12, 36, 80, 150, 252
Sol. Let S = 2 + 12 + 36 + 80 + 150 + 252 + ........ + Tn .... (i)
S = 2 + 12 + 36 + 80 + 150 + 252 + ....... + Tn - 1 + Tn .... (ii)
(i) = (ii) ⇒ Tn = 2 + 10 + 24 + 44 + 70 + 102 + ...... + (Tn - Tn - 1) .... (iii)
Tn = 2 + 10 + 24 + 44 + 70 + 102 + ......... + (Tn - 1 - Tn - 2) + (Tn - Tn - 1) ..... (iv)
(iii) - (iv) ⇒ Tn - Tn - 1 = 2 + 8 + 14 + 20 + 26 + ....
= [4+(n - 1) 6]=n [3n-1] = Tn - Tn - 1 = 3n2 -n
[4+(n - 1) 6]=n [3n-1] = Tn - Tn - 1 = 3n2 -n
∴ general term of given series is 
Hence sum of this series is
S = 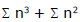 =
=  =
=  (3n2 + 7n + 2)
(3n2 + 7n + 2)  n (n + 1) (n + 2) (3n + 1)
n (n + 1) (n + 2) (3n + 1)
Ex.42 Find the general term and sum of n terms of the series 9, 16, 29, 54, 103
Sol. Let S = 9 + 16 + 29 + 54 + 103 + .......... + Tn .... (i)
S = 9 + 16 + 29 + 54 + 103 + ............+ Tn - 1 + Tn .... (ii)
(i) - (ii)⇒ Tn = 9 + 7 + 13 + 25 + 49 + .......... + (Tn - Tn - 1) .... (iii)
Tn = 9 + 7 + 13 + 25 + 49 + ........ + (Tn-1 - Tn - 2) + (Tn - Tn - 1) .... (iv)
(iii) - (iv) ⇒ Tn - Tn - 1 = 9 + (-2) +  = 7 + 6 [2n - 2 - 1] = 6(2)n - 2 +1.
= 7 + 6 [2n - 2 - 1] = 6(2)n - 2 +1.
∴ General term is Tn = 6(2)n - 1 + n + 2
Also sum S = STn = 6S2n - 1 + Sn + S2 = 6.  + 2n = 6(2n - 1) +
+ 2n = 6(2n - 1) + 
Ex.43 The nth term, an of a sequence of numbers is given by the formula an = an - 1 + 2n for 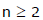 and a1 = 1. Find an equation expressing an as a polynomial in n. Also find the sum to n terms of the sequence.
and a1 = 1. Find an equation expressing an as a polynomial in n. Also find the sum to n terms of the sequence.
Sol. a1 = 1 ; a2 = a1 + 4 = 1 + 4 = 5 ; a3 = a2 + 6 = 5 + 6 = 11 ; a4 = a3 + 8 = 11 + 8 = 19 and so on
hence S = 1 + 5 + 11 + 19 + ........ + an
S = + 1 + 5 + 11 + ........ + an - 1 + an
( - ) ————————————————
0 = 1 + 4 + 6 + 8 + ........ + (an - an - 1) - an
an = 1 + 2
an = 1 +  [4 + (n - 2)] = 1 + (n - 1) (n + 2) = n2 + n - 1
[4 + (n - 2)] = 1 + (n - 1) (n + 2) = n2 + n - 1
sum =  =
=  +
+  -
-  =
= +
+ - n
- n  [(n + 1)(2n + 1) + 3(n + 1) - 6]
[(n + 1)(2n + 1) + 3(n + 1) - 6]
=  [2n2 + 3n + 1 + 3n + 3 - 6] =
[2n2 + 3n + 1 + 3n + 3 - 6] =  [2n2 + 6n - 2] =
[2n2 + 6n - 2] = 
Ex.44 Find the nth term of the series 1 + 2 + 5 + 12 + 25 + 46 + .....
Sol. Let the sum of the series by Sn and nth term of the series be Tn
Then Sn = 1 + 2 + 5 + 12 + 46 + ...+Tn -1 + Tn ...(1)
∴ Sn = 1 + 2 + 5 + 12 + 25 +.... +Tn - 1 + Tn ...(2)
Subtracting (2) from (1), we get 0 = 1 + 1 + 3 + 7 + 13 + 21 + .... + (Tn - Tn - 1) - Tn
∴ Tn = 1 + 3 + 7 + 13 + 21 + ....+tn - 1 + tn ...(3)
(Here nth term of Tn is tn)
∴ Tn = 1 + 1+ 3 + 7 + 13 + .... tn - 1 + tn ...(4)
Subtracting (4) from (3), we get 0 = 1 + 0 + 2 + 4 + 6 + 8 + .... +(tn - tn - 1) - tn
∴ tn = 1 + 2 + 4 + 6 + 8 +....(n - 1) terms = 1 + (2 + 4 + 6 + 8 (n - 2) terms)
= 1 +  {2.2 + (n - 2 - 1) 2} = 1 + (n - 2) (2 + n - 3) ∴ tn = n2 - 3n + 3
{2.2 + (n - 2 - 1) 2} = 1 + (n - 2) (2 + n - 3) ∴ tn = n2 - 3n + 3
then Tn = Stn = Sn2 - 3 S n + 3 S 1 = 
=  {2n2 + 3n + 1 - 9n - 9 + 18}
{2n2 + 3n + 1 - 9n - 9 + 18}  Tn =
Tn =  (2n2 - 6n + 10)=
(2n2 - 6n + 10)=  (n2 - 3n + 5)
(n2 - 3n + 5)
Alternative Method : The nth terms of the series can be written directly from the following procedure
1, 2, 5, 12, 25, 46,...... (given series)
1, 3, 7, 13, 21,..... (first consecutive differences)
2, 4, 6, 8,.... (second consecutive differences)
2, 2, 2,.... (constant terms)
then Tn = a (n - 1) (n - 2) (n - 3) + b (n - 1) (n - 2) + c(n - 1) + d
Putting n = 1, 2, 3, 4 then we get T4 = 6a + 6b + 3c + d = 12
 a =
a =  , b = 1, c = 1, d = 1 Hence Tn =
, b = 1, c = 1, d = 1 Hence Tn =  (n2 - 3n + 5)
(n2 - 3n + 5)
Ex.45 The squares of the natural numbers are grouped like (12); (22, 32, 42); (52, 62, 72, 82, 92); and so on. Find the sum of the elements in nth group.
Sol. By observations, the last element of the nth group = (n2)2
The number of elements in nth group = (2n - 1)
The first element of the nth group = (n2 - 2n + 2)2
Hence sum of the numbers in nth group are
S = (n2 - 2n + 2)2 + (n2 - 2n + 3)2 + ..... + (n2)2
⇒ S = [12 + 22 + 32 + ..... (n2)2] - [12 + 22 + 32 + ((n - 1)2)2]
⇒ S = 
Ex.46 The natural numbers are arranged in groups as given below ;

Prove that the sum of the numbers in the nth group is 2n - 2 {2n + 2n - 1 - 1} .
Sol . Note that nth group has 2n - 1 terms .1st term in the nth group is 2n - 1 and the last term in the nth group is 2n - 1 .
∴ sum of the terms in the nth group

|
75 videos|238 docs|91 tests
|
FAQs on Summation of Series - Mathematics (Maths) Class 11 - Commerce
| 1. What is a summation of series? |  |
| 2. How do you calculate the sum of an arithmetic series? |  |
| 3. What is the formula for finding the sum of a geometric series? |  |
| 4. Can the sum of an infinite series be calculated? |  |
| 5. Are there any other methods to calculate the sum of a series? |  |

|
Explore Courses for Commerce exam
|

|

















