Surface Area & Volume of Right Circular Cylinder | Mathematics for EmSAT Achieve PDF Download
Surface Area of a Cylinder
The surface area of a cylinder is the area occupied by its surface in a three-dimensional space. A cylinder is a three-dimensional structure having circular bases which are parallel to each other. It does not have any vertices. Generally, the area of the three-dimensional shapes refers to the surface area. The surface area is represented in square units. For example, cm2, m2, and so on. A cylinder can be seen as a set of circular disks that are stacked on one another. Since the cylinder is a solid of a three-dimensional shape, it has both surface area and volume.
The cylinder area is defined as the sum of the curved surface and the area of two circular bases of the cylinder.
The Surface Area of Cylinder = Curved Surface + Area of Circular bases
S.A. (in terms of π) = 2πr (h + r) sq.unit
Where, π (Pi) = 3.142 or = 22/7
r is the radius of the cylinder
h height of the cylinder
As we know, a cylinder has two types of surfaces, one is the curved surface and the other is the circular base. So the total surface area will be the sum of the curved surface and two circular bases.
Cylinder Area Definition
The area of the cylinder is the total region covered by a cylinder in three-dimensional space. The cylinder area is equal to the sum of the area of two circular bases and curved surface area. In right cylinders, the two circular bases are exactly over each other and the axis line produces a right angle to the base. In case, if one of the circular bases is displaced and the axis does not produce the right angle to the base, then it is called the oblique cylinder.
In the middle of the two circular bases, there is a curved surface, which, when opened represents a rectangular shape. This curved surface is also called lateral surface. The different parameters that are used to calculate the cylinder area include radius, height, axis, base, and side. The radius of the cylinder is defined as the radius of the circular base. The height of the cylinder is calculated by measuring the perpendicular distance between two circular bases, and the line that joins the centre of the base is called the axis.
Area of a Cylinder Formula
The total area of a cylinder is based on:
- Curved Surface Area (CSA)
- Base Area
1. Curved Surface Area
The curved surface area of a cylinder (CSA) is defined as the area of the curved surface of any given cylinder having base radius ‘r’, and height ‘h’, It is also termed as Lateral surface area (LSA). The formula for a curved area or lateral area is given by;
CSA or LSA = 2π × r × h Square units
2. Base Area of Cylinder
The base of the cylinder is in a circular shape. Hence, by the formula of area of the circle, we know,
Area of the circular bases of cylinder = 2 (πr2) [Since the cylinder has two circular bases]
Total Surface Area of Cylinder
The total surface area of a cylinder is equal to the sum of areas of all its faces. The Total surface area with radius ‘r’, and height ‘h’ is equal to the sum of the curved area and circular areas of the cylinder.
TSA = 2π × r × h + 2πr2 = 2πr (h + r) Square units
Derivation of Surface Area of Cylinder
Now, think of a scenario where we need to paint the faces of a cylindrical container. Before we start painting, we need to know the quantity of paint required for painting all the walls. Thus, we need to find the area of all the faces of this container to calculate the amount of paint needed. We define this term as the total surface area.
Let us take a cylinder of base radius ‘r’ and height ‘h’ units. The curved surface of this cylinder, if opened along the diameter (d = 2r) of the circular base can be transformed into a rectangle of length ‘2πr’ and breadth ‘h’ units.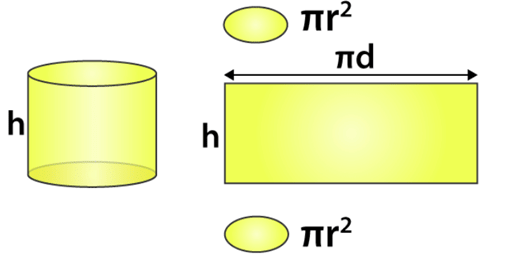
By the formula of area of the circle, we know,
Area of the circular base of cylinder = πr2
Since there are two circular bases, therefore the area of both the circular bases = πr2 + πr2 = 2πr2 ……………….(1)
Now, from the figure you can see, when we open the curved surface of the cylinder in two-dimension space, it forms a rectangle. Hence, the height and circumference of the circular bases are the dimensions of the rectangle formed from it. Therefore,
Area of the curved surface = Height x Circumference
Curved Surface area = h x πd = h x 2πr (since d = 2r)
CSA = 2πrh …………….(2)
By adding equation 1 and equation 2, we get the total surface area, such that;
Total Surface area = Curved Surface area + Area of Circular bases
TSA = 2πrh + 2πr2
By taking 2πr as a common factor from RHS, we get;
TSA = 2πr (h + r)
This is the formula for the total surface area of a given cylinder whose radius is r and height is h.
Problems and Solutions
Q.1. Calculate the cost required to paint a container which is in the shape of a right circular cylinder having a base radius of 7 m and height 13 m. If the painting cost of the container is INR 2.5/m2. (Take π = 22 / 7)
Solution: Total surface area of aquarium = 2πr (h + r)= 2 x 22 / 7 x 7 x 20 = 880 m2
Total cost of painting the container = 2.5 × 880 = Rs. 2200.
Q.2. Find the total surface area of a container in cylindrical shape whose diameter is 28 cm and height is 15 cm.
Solution: Given, diameter = 28 cm, so radius = 28/2 = 14 cm
and height = 15 cm
By the formula of total surface are, we know;
TSA = 2πr (h + r) = 2 x 22 / 7 x 14 x (15 + 14)
TSA = 2 x 22 x 2 x 29
TSA = 2552 sq.cm
Hence, the total surface area of container is 2552 sq.cm.
Volume of a Cylinder
The volume of a cylinder is the density of the cylinder which signifies the amount of material it can carry or how much amount of any material can be immersed in it. Cylinder’s volume is given by the formula, πr2h, where r is the radius of the circular base and h is the height of the cylinder. The material could be a liquid quantity or any substance which can be filled in the cylinder uniformly.
Volume of cylinder has been explained in this briefly along with solved examples for better understanding. In Mathematics, geometry is an important branch where we learn the shapes and their properties. Volume and surface area are the two important properties of any 3d shape.
Definition
The cylinder is a three-dimensional shape having a circular base. A cylinder can be seen as a set of circular disks that are stacked on one another. Now, think of a scenario where we need to calculate the amount of sugar that can be accommodated in a cylindrical box.
In other words, we mean to calculate the capacity or volume of this box. The capacity of a cylindrical box is basically equal to the volume of the cylinder involved. Thus, the volume of a three-dimensional shape is equal to the amount of space occupied by that shape.
Volume of a Cylinder Formula
A cylinder can be seen as a collection of multiple congruent disks, stacked one above the other. In order to calculate the space occupied by a cylinder, we calculate the space occupied by each disk and then add them up. Thus, the volume of the cylinder can be given by the product of the area of base and height.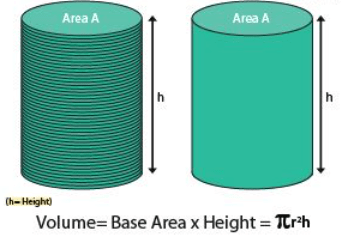 For any cylinder with base radius ‘r’, and height ‘h’, the volume will be base times the height.
For any cylinder with base radius ‘r’, and height ‘h’, the volume will be base times the height.
Therefore, the cylinder’s volume of base radius ‘r’, and height ‘h’ = (area of base) × height of the cylinder
Since the base is the circle, it can be written as
Volume = πr2 × h
Therefore, the volume of a cylinder = πr2h cubic units.
Volume of Hollow Cylinder
In case of hollow cylinder, we measure two radius, one for inner circle and one for outer circle formed by the base of hollow cylinder. Suppose, r1 and r2 are the two radii of the given hollow cylinder with ‘h’ as the height, then the volume of this cylinder can be written as;
V = πh(r12 – r22)
Surface Area of Cylinder
The amount of square units required to cover the surface of the cylinder is the surface area of the cylinder. The formula for the surface area of the cylinder is equal to the total surface area of the bases of the cylinder and surface area of its sides.
A = 2πr2 + 2πrh
Volume of Cylinder in Litres
When we find the volume of the cylinder in cubic centimetres, we can convert the value in litres by knowing the below conversion, i.e.,
1 Litre = 1000 cubic cm or cm3
For example: If a cylindrical tube has a volume of 12 litres, then we can write the volume of the tube as 12 × 1000 cm3 = 12,000 cm3.
Examples
Q.1. Calculate the volume of a given cylinder having height 20 cm and base radius of 14 cm. (Take π = 22 / 7)
Solution: Given:
Height = 20 cm
radius = 14 cm
we know that;
Volume, V = πr2h cubic units
V = (22 / 7) × 14 × 14 × 20
V = 12320 cm3
Therefore, the volume of a cylinder = 12320 cm3.
Q.2. Calculate the radius of the base of a cylindrical container of volume 440 cm3. Height of the cylindrical container is 35 cm. (Take π = 22 / 7)
Solution: Given:
Volume = 440 cm3
Height = 35 cm
We know from the formula of cylinder;
Volume, V = πr2h cubic units
So, 440 = (22 / 7) × r2 × 35
r2 = (440 × 7) / (22 × 35) = 3080 / 770 = 4
Therefore, r = 2 cm
Therefore, the radius of a cylinder = 2 cm.
|
141 videos|213 docs|254 tests
|
FAQs on Surface Area & Volume of Right Circular Cylinder - Mathematics for EmSAT Achieve
| 1. What is the formula for finding the surface area of a right circular cylinder? |  |
| 2. How can I find the volume of a right circular cylinder? |  |
| 3. Can you provide an example of finding the surface area of a right circular cylinder? |  |
| 4. Is there any relationship between the surface area and volume of a right circular cylinder? |  |
| 5. How can I use the formulas for surface area and volume to solve real-life problems involving right circular cylinders? |  |

|
Explore Courses for EmSAT Achieve exam
|

|

















