Tachometric Surveying | Civil Engineering SSC JE (Technical) - Civil Engineering (CE) PDF Download
Surveying (Part 7)
Vertical Curve: A curve used to connect two different grade lines of railways or highways is called a vertical curve.Such a curve is introduced to obtain a gradual change in the gradient so that the vehicles passing over it may not experience a shock or a sudden jerk. It is expressed there as a percentage or as a ratio.
As a percentage : Vertical rise or fall per 100 horizontal e.g. 1%, 2%, 3%. etc.
As a ratio : One vertical rise or fall in n horizontals e.g. 1 in 200, 1 in 500 etc.
Classification of Grades: The grade are further classified into following two categories:
(i) Up - grades or positive grades,
(ii) Down grades or negative grades
Slopes of vertical curves : Depending upon the different combination of different grades, the following six types of vertical curve, are generally used while executing a rail or highway project.
An up grade (+ g1%) followed by a downgrade (– g2%)
A down grade (-g1%) followed by an upgrade(+g2%)
Length of the transition curve,
L=(g1+g2)/r , -(g1+g2)/r

If both rising then,

TACHEOMETRIC SURVEYING:
Tacheometry is the branch of surveying in which both horizontal and vertical distances between stations are determined from instrumental observations.
Horizontal distances obtained by tacheometric observations do not require slope correction, tension correction etc. This method is very rapid and convenient. Though accuracy of tachometric distances is low as compared to direct chaining on flat ground but the accuracy achievable by tacheometry is better as compared to chaining in broken grounds, deep ravines or across large water bodies.
The instrument employed for tacheometric purpose, is generally known as a tacheometer which is similar to theodolite having diaphragm fitted with two additional horizontal wires, called stadia hairs.
Whenever surveys of higher accuracy are carried out, tacheometry provides a good check on distances measured with a tape or a chain.
Instruments Used for Tachometric Surveying :
1. Tacheometer : It is a transit theodolite fitted with stadia diagram.The stadia diagram consists of two stadia hairs at equal distances,one above and one below the horizontal hair of the cross-hair.
2. Stadia rods : For short sights of about 100 m or less, an ordinary levelling staff may be used. For long sights, special staff called stadia rod is generally used. The graduations are in bold type (face about 50 mm to 150 mm wide and 15 mm to 60 mm thick) and the stadia rod is 3 m to 5 m long. To keep the staff or stadia rod vertical, a small circular spirit level is fitted on its backside. It is hinged to fold up.
SYSTEMS OF TACHEOMETRIC MEASUREMENTS :
The underlying principle common to various systems of tacheometry is that the horizontal distance between an instrument station P and a point Q, as well as the elevation of Q relative to the instrument, can be deduced from
(a) the angle at P subtended by a known small distance at Q, and
(b) the vertical angle from P to Q.
This basic principle is applied in different ways in different tacheometric methods. There are basically three systems of tacheometric measurements described below:
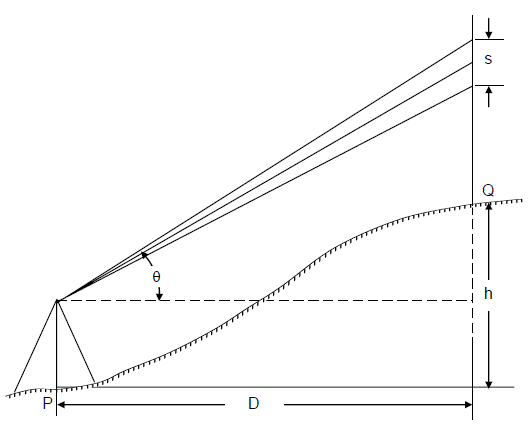
(i) Stadia hair system: This is the more extensively used system of tacheometry particularly for detailed work, such as those required in engineering surveys. In this system, a tacheometer is first set up at a station, say P, and a staff is held at station Q, as shown in Figure below. The difference of upper hair reading and lower hair reading is called staff intercept s. All the three hairs including central cross hair are read, and s is determined. Vertical angle, θ, corresponding to the central hair is also measured. These measurements enable determination of horizontal distance between P and Q and their difference in elevation. There are two different types of systems in stadia method. These are as follows :
(a) Fixed hair method: In this method, the distance between the upper hair and lower hair, i.e. stadia interval i, on the diaphragm of the lens system is fixed. The staff intercept s, therefore, changes according to the distance D and vertical angle θ.
(b) Movable hair method: In this method, the stadia interval ‘i’ can be changed. The stadia hairs can be moved vertically up and down by using micrometer screws. The staff intercept s, in this case, is kept fixed. Two vanes (targets) are fixed on the staff at a fixed interval of 2 m or 3 m.
The fixed hair method is the one which is commonly used and, unless otherwise mentioned, stadia method means fixed hair method. Movable hair method is not in common use due to difficulties in determining the value of i accurately.
 The Stadia System
The Stadia System
(ii) Tangential system
(iii) Subtense bar system
Principle of Tacheometry Surveying : The main principle of Tacheometry is based on the basic principle of isosceles triangle.In any two side equal triangle means isoceles triangle, there is one property which is used in the Tacheometry.
It states that,
Ratio of the perpendicular to vertex on their base and their base is always constant in isoceles triangle.
-It means if object is far from vertex than it cover more area and if it is near than it cover less area because ratio is constant.
-By this principle, Tacheometer works.
-There is object which is far from instrument but if we take reading in instrument then it appears as low distance in diaphragm.
Basic Principle of Stadia Method:
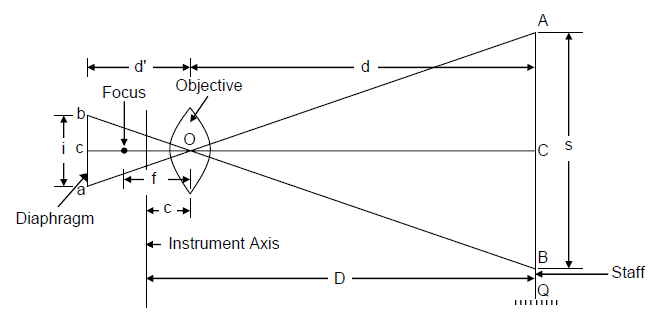
We will derive distance and elevation formulae for fixed hair method assuming line of sight as horizontal and considering an external focusing type telescope. In Figure below, O is the optical centre of the object glass. The three stadia hairs are a,b and c and the corresponding readings on staff are A, B and C. Length of image of AB is ab. The other terms used in this figure are
f = focal length of the object glass,
i = stadia hair interval = ab,
s = staff intercept = AB,
c = distance from O to the vertical axis of the instrument,
d = distance from O to the staff,
d′′ = distance from O to the plane of the diaphragm, and
D = horizontal distance from the vertical axis to the staff.
 Principle of Stadia Method
Principle of Stadia Method
From similar Δs, AOB and aOb, we get
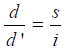
And from lens formula,
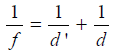
Combining the two equations, we get
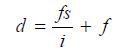
Adding c to both the sides
Or 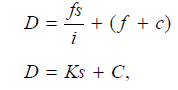
where the constant K is equal to (f /i). It is called multiplying constant of the tacheometer and is generally kept as 100. The constant C is equal to (f + c). It is called additive constant whose value ranges from 30 cm to 50 cm for external focusing telescopes and 10 cm to 20 cm for internal focusing telescopes. For telescopes fitted with anallactic lens, C equals zero.
Elevation of the staff station Q can be determined as in simple levelling, using the central hair reading C and knowing the Reduced Level (RL) of the plane of collimation.
Various Cases – Inclined Sights with Staff Vertical and Staff Normal to the Line of Sight:
In stadia tacheometry with fixed hair method, horizontal sights may not always be available, particularly in rough and hilly terrain where differences of elevation between the instrument and staff stations are large. The measurements involve recording of vertical angle (elevation or depression) to the central stadia hair in addition to the staff intercept. There may be two cases one in which staff is held vertical and another in which staff is held normal to the line of sight. Generally, the former is preferred.
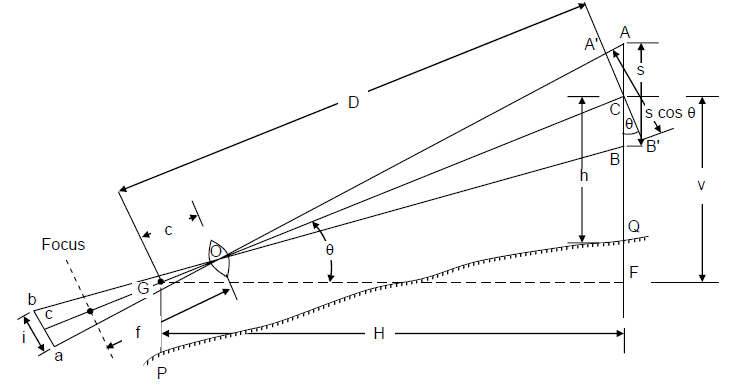
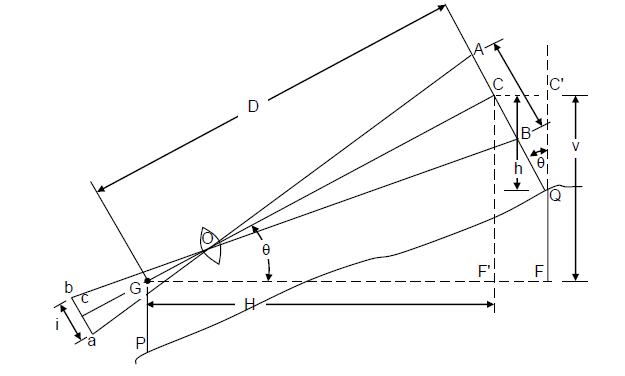
Staff Vertical:
In Figure below, θ is the angle of elevation of the line of sight. Let us draw an intercept A′B′ through C perpendicular to OC. Now ACA′ = θ and AA′C may be taken practically equal to 90o. A′B′ may, therefore, be expressed as s. cos θ with small error, which can be neglected. Now, distance OC = D can be expressed as
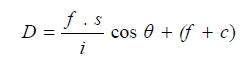
and the required horizontal distance H will be
H = D cos θ,
Or, 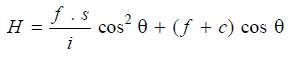
 Inclined Sights – Staff Vertical
Inclined Sights – Staff Vertical
For determination of elevation difference between P and Q, it is necessary to determine the value of V, i.e. FC, which is the difference of levels between the collimation plane and the point C (i.e. central hair reading) on the staff.
Now V = D . sin θ or H . tan θ
Or, 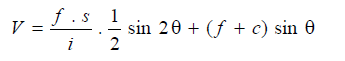
Denoting QC, the central hair reading as h, the level difference between G and Q for an angle of elevation is given by
FQ = V − h
and if θ is angle of depression,
FQ = V + h
Now, if we express the level of collimation line above datum by Height of Instrument (HI), then
RL of Q = HI + V − h
In case of a depressed sight
RL of Q = HI – V − h
Staff Normal:
Figure below shows the situation when the staff is held normal to the line of sight. Some sighting device is attached to the staff to enable the staffman to hold the staff normal to the line of sight. If no sighting device is attached, the inclination of the staff may be adjusted till the staff intercept is minimum
In this case, 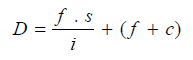
but H = D cos θ + CC′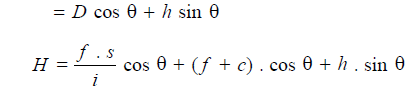
In case of angle of depression, h sin θ term will be subtractive, since the staff is held away from the instrument.
Now, V = F′ C = D sin θ
Or, 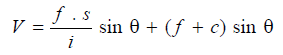
For an angle of elevation,
FQ = V − h. cos θ,
and RL of Q = HI + V − h cos θ
And for an angle of depression,
FQ = V + h cos θ,
and RL of Q = HI − V − h cos θ
where HI is height of instrument at P above datum
 Inclined Sight – Staff Normal
Inclined Sight – Staff Normal
TYPE OF TELESCOPE FITTED IN STADIA THEODOLITE :
The telescope used in stadia theodolites are of the following three types :
(i) Internal focusing telescope
(ii) External focusing telescope
(iii) Internal focusing telescope fitted with an anallatic lens. (C = 0) The theodolite fitted with the second type is known as stadia theodolite whereas that fitted with third type is known as a tacheometer. In a tacheometer, additive constant is usually kept zero.
A TACHEOMETER MUST MEET THE FOLLOWING REQUIREMENTS :
(i) The multiplying constant (K) must be 100 and the error in the computed distance should not exceed 1 in 1000 .
(ii) The central hair should be exactly midway between the stadia hair.
(iii) The telescope must be truly analectic. (C = 0). That is analectic constant or additive constant (C) must be zero.
MOVABLE HAIR METHOD : In movable hair method, the staff intercept s is fixed, whereas the variable stadia-hair interval is adjusted by the use of micrometer screws. The upper and lower stadia hairs should simultaneously bisect the target ends on the staff. The interval i so measured enables determination of horizontal distance.
The expression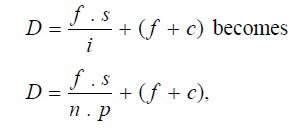
where p = pitch of the screws, and
n = number of pitches between the stadia hairs or the number of turns necessary to move the stadia hairs until they subtend s on the staff.
This expression involves the two instrumental constants (f/p) and (f + c). A tacheometer with movable stadia hairs is called a Subtense Theodolite.
|
2 videos|122 docs|55 tests
|
FAQs on Tachometric Surveying - Civil Engineering SSC JE (Technical) - Civil Engineering (CE)
| 1. What is tachometric surveying in civil engineering? |  |
| 2. How does tachometric surveying differ from traditional surveying methods? |  |
| 3. What are the advantages of using tachometric surveying in civil engineering projects? |  |
| 4. Are there any limitations or challenges associated with tachometric surveying? |  |
| 5. How is tachometric surveying used in civil engineering projects? |  |
|
2 videos|122 docs|55 tests
|



















