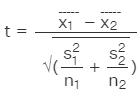T-Test | Applied Mathematics for Class 12 - Commerce PDF Download
| Table of contents |

|
| T-test Formula |

|
| What Is the T-test Formula? |

|
| One-Sample T-Test Formula |

|
| Independent Sample T-Test |

|
| Paired Samples T-Test |

|
| Examples Using t-test Formula |

|
T-test Formula
The t-test formula helps us to compare the average values of two data sets and determine if they belong to the same population or are they different. The t-score is compared with the critical value obtained from the t-table. The large t-score indicates that the groups are different and a small t-score indicates that the groups are similar.
What Is the T-test Formula?
The t-test formula is applied to the sample population. The t-test formula depends on the mean, variance, and standard deviation of the data being compared. There are 3 types of t-tests that could be performed on the n number of samples collected.
- One-sample test,
- Independent sample t-test and
- Paired samples t-test
The critical value is obtained from the t-table looking for the degree of freedom(df = n-1) and the corresponding α value(usually 0.05 or 0.1). If the t-test obtained statistically > CV then the initial hypothesis is wrong and we conclude that the results are significantly different.
One-Sample T-Test Formula
For comparing the mean of a population
 from n samples, with a specified theoretical mean μ, we use a one-sample t-test.
from n samples, with a specified theoretical mean μ, we use a one-sample t-test.
where σ/√n is the standard error
w here,
`x' bar is the mean of the sample,
N is the assumed mean,
σ is the standard deviation
and n is the number of observations
Independent Sample T-Test
Students t-test is used to compare the mean of two groups of samples. It helps evaluate if the means of the two sets of data are statistically significantly different from each other.


where
- t = Student's t-test
- x1 = mean of first group
- x2 = mean of second group
- s1 = standard deviation of group 1
- s2 = standard deviation of group 1
- n1 = number of observations in group 1
- n2 = number of observations in group 2
Paired Samples T-Test
Whenever two distributions of the variables are highly correlated, they could be pre and post test results from the same people. In such cases, we use the paired samples t-test.

where
t = Student's t-test
x1 − x2 = Difference mean of the pairs
s = standard deviation
n = sample size
Examples Using t-test Formula
Example 1: Calculate a t-test for the following data of the number of times people prefer coffee or tea in five time intervals.

let x1 be the sample of data that prefers coffee and x2 be the sample of data that prefers tea.
let us find the mean, variance and the SD
According to the t-test formula,
Applying the known values in the t-test formula, we get
t = 0.47
Example 2: A company wants to improve its sales. The previous sales data indicated that the average sale of 25 salesmen was $50 per transaction. After training, the recent data showed an average sale of $80 per transaction. If the standard deviation is $15, find the t-score. Has the training provided improved the sales?
H0 accepted hypothesis:the population mean = the claimed value ⇒ μ = μ0
H0 alternate hypothesis: the population mean not equal to the claimed value ⇒ μ ≠ μ0
t-test formula for independent test is
Mean sale = 80, μ = 50, s = 15 and n = 25
substituting the values, we get t = (80-50)/(15/√25)
t = (30 ×5)/10 = 10
looking at the t-table we find 10 > 1.711 . (I.e. CV for α = 0.05).
∴ the accepted hypothesis is not true. Thus we conclude that the training boosted the sales.
Example 3: A pre-test and post-test conducted during a survey to find the study hours of Patrick on weekends. Calculate the t-score and determine (for α = 0.25) if the pre-test and post-test surveys are significantly different?
According to the t-test formula, we know that
Σ(X-Y)= -3 = 3
s = Σ(X-Y)2/(n-1) = 52/1 = 25
t = 3/(25/2) = 6/25 = 0.24
here degree of freedom is n-1 = 2-1 =1 and the corresponidng critical value in the t-table for α = 0.25, is 1.
t < CV.
Therefore the scores are not significantly different.
|
58 videos|101 docs|63 tests
|

|
Explore Courses for Commerce exam
|

|