The Complex Plane - Complex Analysis, CSIR-NET Mathematical Sciences | Mathematics for IIT JAM, GATE, CSIR NET, UGC NET PDF Download
Complex numbers are defined as tuples (x,y) or equivalently x+iy. Therefore is is natural to visualize them as objects in the two-dimensional plane.
Definition 1.2.1: The Complex Plane
The field of complex numbers is represented as points or vectors in the two-dimensional plane. If z = (x,y) = x+iy is a complex number, then x is represented on the horizonal, y on the vertical axis. The horizontal axis is called real axis while the vertical axis is the imaginary axis.
Visually, C looks like R2, and complex numbers are represented as "simple" 2-dimensional vectors. Even addition is defined just as addition in R2. The big difference between C and R2, though, is the definition of multiplication. In R2 no multiplication of vectors is defined. To be precise, there is the idea of dot-product and (if you think of R2 as embedded in R3) cross-product, but the definition of complexmultiplication gives C its special structure.
Before we explore multiplication further, let's define a few easier operations in C and see their impact in the complex plane.
|
Definition 1.2.3: Re, Im, Conj, and Modulus If z = x + iy is a complex number, then we define the following functions: The Real Part Re: C The Imaginary Part Im: C The Conjugate or z-bar conj: C The Modulus, or Absolute Value |.|: C |
Geometrically, these operations are easy to visualize:
- Re(z) is the projection of z onto the real axis
- Im(z) is the projection of z onto the imaginary axis
- conj(z) is the vector z reflected around the real axis
- |z| is the standard Euclidean length of the vector z, using good old Pythagoras
Our new operations can also be composed with one another:
Similar relations hold when composing the conjugate function, but since we will need these identities frequently we will state them in the form of a proposition:
|
Proposition 1.2.6: The conjugate operator For every complex number z we have: (1) |z| = |conj(z)| = | (2) |z|2 = z*conj(z) = z (3) conj(conj(z)) = ( |
Addition and in particular multiplication are what really define the structure of the complex plane and we need to figure out how to visualize those operations. Addition (and subtraction) will be familiar from vectors in the plane:
|
Proposition 1.2.7: Adding complex numbers geometrically For any complex numbers z and w you can find the sum z+w by attaching the vector w to the tip of the vector z and completing a paralellogram. The diagonal of that paralellogram is the vector z+w. To find the difference z-w, reverse the vector w and find z+(-w). Proof: You can easily verify this by writing z and w as vectors in R2.
|
Multiplication is more difficult to figure out, but feel free to come up with a conjecture before reading on.
To see if your conjecture about multiplication is correct, we first need to introduce a more suitable coordinate system. Similar to vectors in the 2-D plane, we define polar coordinates as follows:
|
Definition 1.2.9: Polar coordinates and cis A complex, non-zero number z=x+iy with rectangular coordinates (x,y) can also be represented in polar coordinates (r,t). Let and t be an angle such that x = r cos(t) und y = r sin(t) Then z = x+iy = r cos(t) + i r sin(t) = r (cos(t)+i sin(t)) = r cis(t) where we define cis(t) = cos(t) + i sin(t). r is called the radius or length, t the angle or argument of z. |
|
Sample points
It is easy to convert a number z from polar coordinates (r,t) to rectangular coordinates (x,y): simply use the fact that z = r cis(t) = r(cos(t) + i sin(t)), i.e. compute
- x = r cos(t)
- y = r sin(t)
You can verify, for example, that the complex number with polar coordinates r=2 and angle t=π/4 can be written in rectangular coordinates as
z = 2 cis(π/4) = 2 (cos(π/4) + i sin(π/4)) = 2 (1/√2 + i 1/√2) = √2 + i √2
Going the other way, i.e. converting from rectangular to polar coordinates, is a little more confusing since the angle in the above definition is not unique. For example, the complex number 1+i clearly has a radius of √2 but any angle π/4 + 2kπ will work. In other words, z=1+i=(1,1) in rectangular coordinates is equal to
(√2,π/4) = (√2,9π/4) = (√2,17π/4) = ...
in polar coordinates. To avoid confusion, we will often (somewhat arbitrarily) restrict the angle of a complex number in polar coordinates to be between -π and π and call it principle angle.
|
Definition 1.2.10: The Principle Argument Arg For any complex number z ≠ 0 we define the principle argument or Arg(z) as the angle which the vector z makes with the positive (real) x-axis and for which -π < Arg(z) < π |
In other words, a non-zero complex number has many arguments, but only one principle argument. To find a principle argument we use the fact that
tan(t) = sin(t)/cos(t) = r sin(t)/r cos(t) = y/x = Im(z)/Re(z)
so that we can use the tan-1 = arctan adjusted in such a way as to give us the principle angle: take any non-zero complex number z:
If Re(z) = 0 then
- if Im(z) > 0 then Arg(z) = π/2
- if Im(z) < 0 then Arg(z) = -π/2
If Re(z) ≠ 0 compute
and adjust the angle as follows:
- for z in 1st quadrant: Arg(z) = α
- for z in 2nd quadrant: Arg(z) = π - α
- for z in 3rd quadrant: Arg(z) = -π + α
- for z in 4th quadrant: Arg(z) = -α
Using polar coordinates will finally allow us to understand how multiplication of complex numbers works geometrically:
|
Theorem 1.2.12: Multiplying complex numbers geometrically If z = r1 cis(s) and w = r2 cis(t) in polar coordinates then z*w = r1 r2 cis(s + t) and zn = rn cis(ns) |
You might wonder why this theorem is called "multiply complex numbers geometrically" when in fact it shows only formulas. But what the formulas mean is:
- two complex numbers are multiplied by multiplying their length and adding their angles
- a complex number is raised to a power by raising the length to the power and multiplying the angle
A similar trick works for division of two complex numbers:
Corollary 1.2.13: Dividing complex numbers geometrically
If z = r1 cis(s) and w = r2 cis(t) in polar coordinates then
z/w = r1 / r2 cis(s - t)
If a complex number z lies on the unit circle it has length one so that z=sin(t)+i cos(t) for somes t (i.e. the radius r is 1. In that case the above theorem has another well-known corollary:
|
Corollary 1.2.15: DeMoivre's Formula For any integer n and any real number t we have (cos(t) + i sin(t))n = cos(nt) + i sin(nt) |
DeMoivre's Formula is quite something. It says that if you take a number on the unit circle (i.e. with lenght 1) with initial argument (angle) t and multiply it by itself, it simply rotates around the unit circle by that angle t. Each time you multiply the number by itself, the vector rotates another t degrees. In other words, in this case the power operator results in a simple rotation.
Two interesting questions related to this rotation, taken from the field of Complex Dynamics, are: suppose z is a complex number with |z|=1. Then:
- find conditions for Arg(z) such that zn = z for some integer n. Such a point, incidentally, is called periodic of order n.
- if Arg(z)/π is irrational, what can you say about the sequence {z, z2, z3, z4, ...}? Does it, for example, converge? Such a sequence, incidentally, is called the orbit of z.
Polar coordinates can be especially helpful for finding roots, in particular for complex numbers of lenght 1.
Proposition 1.2.16: Finding Roots
For any positive integer n and any non-zero complex number a = r cis(t) the equation zn = a has exactly n distinct roots given by:
z =
where k = 0, 1, 2, ... n-1
In a previous example we found the two square roots of i, which turned out to be a fair amount of work. The above proposition allows us to dispense with such a question quickly. For example, the two solutions for
z2 = i = cis(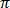 /2)
/2)
are:
z1 = cis(π/2/2) = cis(π/4)
z2 = cis((π/2 + 2π)/2) = cis(5π/4)
which you can quickly check using DeMoivre's Formula. Here is a geometric interpretation of this proposition: let's find, for example, the three third-roots of i, i.e. we want to find all solutions to z3 = i.
| 1: Draw the vector i | 2: Divide angle by 3 for first root | 3: Draw 3 equally spaced segments, starting at the first root |
Note, in particular, that the third root of i turned out to be -i, which indeed checks out:
(-i)(-i)(-i) = i*i*(-i) = (-1)*(-i) = i
This proposition is very satisfying: it says that at least every simple polynomial equation of degree n has n solutions. Later we will see that this is true in general: every n-th degree polynomial has n roots, no "if's" and "but's". This, in fact, is a sign of things to come: many theorems in complex analysis will turn out to be very "satisfying" and nicely structured, which is one reason that the study of complex analysis is a lot of fun (I think -:). But first a few more 'profane' examples.
Let's conclude this chapter with a result that illustrates what a 'nicely structured' theorem in complex analysis can look like.
|
Proposition 1.2.18: Roots of Unity The n n-th roots of unity are given by wnk, where k = 0, 1, 2, ... n-1 and wn = cis(2π/n) They form the vertices of a regular polygon and add up to zero, i.e. they satisfy the equation: 1 + wn + wn2 + ... + wnn-1 = 0 |
This is neat: not only does the equation zn = 1 have exactly n solutions (one of which is, of course, z=1), but the solutions have this really pretty geometric structure of forming a regular polygon, which implies algebraically that they add up to zero as vectors. Here are, for example, the eight roots of z8=1:
|
558 videos|198 docs
|
FAQs on The Complex Plane - Complex Analysis, CSIR-NET Mathematical Sciences - Mathematics for IIT JAM, GATE, CSIR NET, UGC NET
| 1. What is the complex plane in complex analysis? |  |
| 2. What is complex analysis? |  |
| 3. How are complex numbers represented on the complex plane? |  |
| 4. What is the significance of the complex plane in complex analysis? |  |
| 5. How can the complex plane be used in solving problems in mathematics and physics? |  |

 R, Re(z) = Re(x+iy) = x is the real part of z
R, Re(z) = Re(x+iy) = x is the real part of z R, Im(z) = Im(x+iy) = y is the imaginary part of z
R, Im(z) = Im(x+iy) = y is the imaginary part of z C, conj(z) = conj(x+iy) = x - iy is the conjugate of z. The conjugate of z is sometimes also denoted as
C, conj(z) = conj(x+iy) = x - iy is the conjugate of z. The conjugate of z is sometimes also denoted as 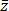 (z-bar)
(z-bar) R, |z| = |x+iy| =
R, |z| = |x+iy| = 















