The Ideal Gas Law | Basic Physics for IIT JAM PDF Download

The air inside this hot air balloon flying over Putrajaya, Malaysia, is hotter than the ambient air. As a result, the balloon experiences a buoyant force pushing it upward. 

In this section, we continue to explore the thermal behavior of gases. In particular, we examine the characteristics of atoms and molecules that compose gases. (Most gases, for example nitrogen, N₂, and oxygen, O₂, are composed of two or more atoms. We will primarily use the term “molecule” in discussing a gas because the term can also be applied to monatomic gases, such as helium.)
Gases are easily compressed. We can see evidence of this in, where you will note that gases have the largest coefficients of volume expansion. The large coefficients mean that gases expand and contract very rapidly with temperature changes. In addition, you will note that most gases expand at the same rate, or have the same β. This raises the question as to why gases should all act in nearly the same way, when liquids and solids have widely varying expansion rates.
The answer lies in the large separation of atoms and molecules in gases, compared to their sizes, as illustrated in. Because atoms and molecules have large separations, forces between them can be ignored, except when they collide with each other during collisions. The motion of atoms and molecules (at temperatures well above the boiling temperature) is fast, such that the gas occupies all of the accessible volume and the expansion of gases is rapid. In contrast, in liquids and solids, atoms and molecules are closer together and are quite sensitive to the forces between them.
Atoms and molecules in a gas are typically widely separated, as shown. Because the forces between them are quite weak at these distances, the properties of a gas depend more on the number of atoms per unit volume and on temperature than on the type of atom.

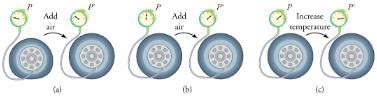
To get some idea of how pressure, temperature, and volume of a gas are related to one another, consider what happens when you pump air into an initially deflated tire. The tire’s volume first increases in direct proportion to the amount of air injected, without much increase in the tire pressure. Once the tire has expanded to nearly its full size, the walls limit volume expansion. If we continue to pump air into it, the pressure increases. The pressure will further increase when the car is driven and the tires move. Most manufacturers specify optimal tire pressure for cold tires.
(a) When air is pumped into a deflated tire, its volume first increases without much increase in pressure. (b) When the tire is filled to a certain point, the tire walls resist further expansion and the pressure increases with more air. (c) Once the tire is inflated, its pressure increases with temperature.

At room temperatures, collisions between atoms and molecules can be ignored. In this case, the gas is called an ideal gas, in which case the relationship between the pressure, volume, and temperature is given by the equation of state called the ideal gas law.

Ideal Gas Law
The ideal gas law states that
PV = NkT,
where P is the absolute pressure of a gas, V is the volume it occupies, N is the number of atoms and molecules in the gas, and T is its absolute temperature. The constant k is called the Boltzmann constant in honor of Austrian physicist Ludwig Boltzmann (1844–1906) and has the value
k = 1.3810^-23 J/K

The ideal gas law can be derived from basic principles, but was originally deduced from experimental measurements of Charles’ law (that volume occupied by a gas is proportional to temperature at a fixed pressure) and from Boyle’s law (that for a fixed temperature, the product PVis a constant). In the ideal gas model, the volume occupied by its atoms and molecules is a negligible fraction of V. The ideal gas law describes the behavior of real gases under most conditions. (Note, for example, that N is the total number of atoms and molecules, independent of the type of gas.)
Let us see how the ideal gas law is consistent with the behavior of filling the tire when it is pumped slowly and the temperature is constant. At first, the pressure P is essentially equal to atmospheric pressure, and the volume V increases in direct proportion to the number of atoms and molecules N put into the tire. Once the volume of the tire is constant, the equation PV = NkT predicts that the pressure should increase in proportion to the number N of atoms and molecules.