The Integer Quantum Hall Effect (Part-2) | Basic Physics for IIT JAM PDF Download
Robustness of the Hall State
The calculations above show that if an integer number of Landau levels are filled, then the longitudinal and Hall resistivities are those observed on the plateaux. But it doesn’t explain why these plateaux exist in the first place, nor why there are sharp jumps between different plateaux.
To see the problem, suppose that we fix the electron density n. Then we only completely fill Landau levels when the magnetic field is exactly 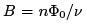 for some integer v. But what happens the rest of the time when
for some integer v. But what happens the rest of the time when 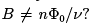 Now the final Landau level is only partially filled. Now when we apply a small electric field, there are accessible states for the electrons to scatter in to. The result is going to be some complicated, out-of-equilibrium distribution of electrons on this final Landau level. The longitudinal conductivity
Now the final Landau level is only partially filled. Now when we apply a small electric field, there are accessible states for the electrons to scatter in to. The result is going to be some complicated, out-of-equilibrium distribution of electrons on this final Landau level. The longitudinal conductivity 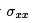 will surely be non-zero, while the Hall conductivity will differ from the quantised value (2.3).
will surely be non-zero, while the Hall conductivity will differ from the quantised value (2.3).
Yet the whole point of the quantum Hall effect is that the experiments reveal that the quantised values of the resistivity (2.3) persist over a range of magnetic field. How is this possible?
The Role of Disorder
It turns out that the plateaux owe their existence to one further bit of physics: disorder. This arises because experimental samples are inherently dirty. They contain impurities which can be modelled by adding a random potential V(x) to the Hamiltonian. As we now explain, this random potential is ultimately responsible for the plateaux observed in the quantum Hall effect. There’s a wonderful irony in this: the glorious precision with which these integers v are measured is due to the dirty, crappy physics of impurities.
To see how this works, let’s think about what disorder will likely do to the system. Our first expectation is that it will split the degenerate eigenstates that make up a Landau level. This follows on general grounds from quantum perturbation theory: any generic perturbation, which doesn’t preserve a symmetry, will break degeneracies. We will further ask that the strength of disorder is small relative to the splitting of the Landau levels,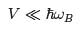 (2.6)
(2.6)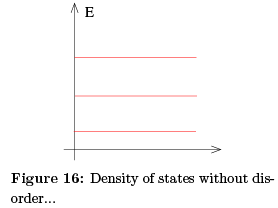
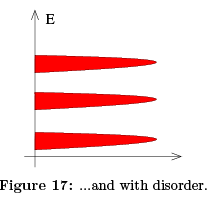
In practice, this means that the samples which exhibit the quantum Hall effect actually have to be very clean. We need disorder, but not too much disorder! The energy spectrum in the presence of this weak disorder is the expected to change the quantised Landau levels from the familiar picture in the left-hand figure, to the more broad spectrum shown in the right-hand figure.
There is a second effect of disorder: it turns many of the quantum states from extended to localised. Here, an extended state is spread throughout the whole system. In contrast, a localised state is restricted to lie in some region of space. We can easily see the existence of these localised states in a semi-classical picture which holds if the potential, in addition to obeying (2.6), varies appreciably on distance scales much greater than the magnetic length lB,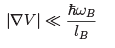
With this assumption, the cyclotron orbit of an electron takes place in a region of essentially constant potential. The centre of the orbit, X then drifts along equipoten-tials. To see this, recall that we can introduce quantum operators (X, Y) describing the centre of the orbit (1.33),
with π the mechanical momentum (1.14). (Recall that, in contrast to the canonical momentum, π is gauge invariant). The time evolution of these operators is given by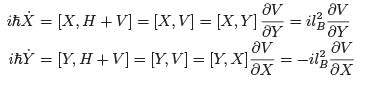
where we used the fact (1.34) that, in the absence of a potential, [X, H] = [Y, H] = 0, together with the commutation relation [X, Y] = il2B (1.35). This says that the centre of mass drifts in a direction (X, Y') which is perpendicular to W; in other words, the motion is along equipotentials.
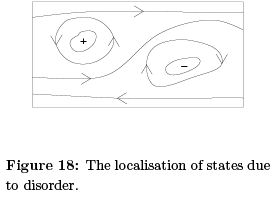
Now consider what this means in a random potential with various peaks and troughs. We’ve drawn some contour lines of such a potential in the left-hand figure, with + denoting the local maxima of the potential and — denoting the local minima. The particles move anti-clockwise around the maxima and clockwise around the minima. In both cases, the particles are trapped close to the extrema. They can’t move throughout the sample. In fact, equipotentials which stretch from one side of a sample to another are relatively rare. One place that they’re guaranteed to exist is on the edge of the sample.
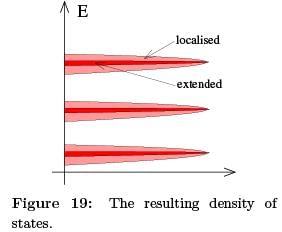
The upshot of this is that the states at the far edge of a band — either of high or low energy — are localised. Only the states close to the centre of the band will be extended. This means that the density of states looks schematically something like the right-hand figure.
Conductivity Revisited
For conductivity, the distinction between localised and extended states is an important one. Only the extended states can transport charge from one side of the sample to the other. So only these states can contribute to the conductivity.
Let’s now see what kind of behaviour we expect for the conductivity. Suppose that we’ve filled all the extended states in a given Landau level and consider what happens as we decrease B with fixed n. Each Landau level can accommodate fewer electrons.
But, rather than jumping up to the next Landau level, we now begin to populate the localised states. Since these states can’t contribute to the current, the conductivity doesn’t change. This leads to exactly the kind of plateaux that are observed, with constant conductivities over a range of magnetic field.
So the presence of disorder explains the presence of plateaux. But now we have to revisit our original argument of why the resistivities take the specific quantised values (2.3). These were computed assuming that all states in the Landau level contribute to the current. Now we know that many of these states are localised by impurities and don’t transport charge. Surely we expect the value of the resistivity to be different. Right? Well, no. Remarkably, current carried by the extended states increases to compensate for the lack of current transported by localised states. This ensures that the resistivity remains quantised as (2.3) despite the presence of disorder. We now explain why.
The Role of Gauge Invariance
Instead of considering electrons moving in a rectangular sample, we’ll instead consider electrons moving in the annulus shown in the figure. In this context, this is sometimes called a Corbino ring. We usually console ourselves by arguing that if the Hall conductivity is indeed quantised then it shouldn’t depend on the geometry of the sample. (Of course, the flip side of this is that if we’ve really got the right argument, that shouldn’t depend on the geometry of the sample either; unfortunately this argument does.)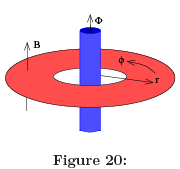
The nice thing about the ring geometry is that it provides us with an extra handle8. In addition to the background magnetic field B which penetrates the sample, we can thread an additional flux  through the centre of the ring. Inside the ring, this
through the centre of the ring. Inside the ring, this  is locally pure gauge. Nonetheless, from our discussion in Section 1.5, we known that
is locally pure gauge. Nonetheless, from our discussion in Section 1.5, we known that 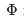 can affect the quantum states of the electrons.
can affect the quantum states of the electrons.
Let’s first see what has to do with the Hall conductivity. Suppose that we slowly increase
has to do with the Hall conductivity. Suppose that we slowly increase  from 0 to
from 0 to  . Here “slowly” means that we take a time
. Here “slowly” means that we take a time 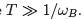 This induces an emf around the ring,
This induces an emf around the ring, 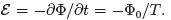 Let’s suppose that we can argue that n electrons are transferred from the inner circle to the outer circle in this time. This would result in a radial current Ir = — ne/T.
Let’s suppose that we can argue that n electrons are transferred from the inner circle to the outer circle in this time. This would result in a radial current Ir = — ne/T.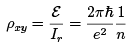 (2.7)
(2.7)
This is the result we want. Our task, therefore, is to argue that n electrons are indeed transferred across the ring as the flux is increased to 
Spectral Flow in Landau Levels
The key idea that we need is that of spectral flow, introduced in Section 1.5.3. The spectrum of the Hamiltonian is the same whenever 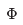 is an integer multiple of
is an integer multiple of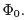 However, if we start with a particular energy eigenstate when
However, if we start with a particular energy eigenstate when 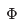 = 0, this will evolve into a different energy eigenstate with
= 0, this will evolve into a different energy eigenstate with 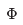 =
= 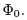 . As the change is done suitably slowly, over a time
. As the change is done suitably slowly, over a time 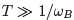 , the adiabatic theorem ensures that the final energy eigenstate must lie in the same Landau level as the initial state.
, the adiabatic theorem ensures that the final energy eigenstate must lie in the same Landau level as the initial state.
To illustrate this, let’s first look at the situation with no disorder. For the ring geometry, it is sensible to use symmetric gauge and radial coordinates,  . The wavefunctions in the lowest Landau level are (1.30),
. The wavefunctions in the lowest Landau level are (1.30),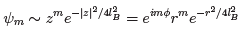
The mth wavefunction is strongly peaked at a radius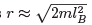 (where, of course, we must now chose m E ∈ Z such that the wavefunction lies inside the annulus). From the discussion in Section 1.5.3, we see that if we increase the flux from
(where, of course, we must now chose m E ∈ Z such that the wavefunction lies inside the annulus). From the discussion in Section 1.5.3, we see that if we increase the flux from 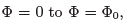 , the wavefunctions shift from m to m + 1,
, the wavefunctions shift from m to m + 1,
This means that each state moves outwards, from radius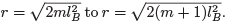 The net result is that, if all states in the Landau level are filled, a single electron is transferred from the inner ring to the outer ring as the flux is increased from Φ = 0 toto Φ = Φ0. It is simple to check that the same result holds for higher Landau levels. If n Landau levels are filled, then n electrons are transferred from the inner to the outer ring and the Hall resistivity is given by (2.7) as required.
The net result is that, if all states in the Landau level are filled, a single electron is transferred from the inner ring to the outer ring as the flux is increased from Φ = 0 toto Φ = Φ0. It is simple to check that the same result holds for higher Landau levels. If n Landau levels are filled, then n electrons are transferred from the inner to the outer ring and the Hall resistivity is given by (2.7) as required.
Spectral Flow in the Presence of Disorder
The discussion above merely reproduces what we already know. Let’s now see how it changes in the presence of disorder. In polar coordinates, the Hamiltonian takes the form 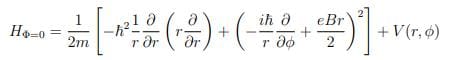
where V (r, φ) is the random potential capturing the effects of disorder. Note that this depends on φ, so angular momentum is no longer a good quantum number in this system. Adding the flux through the centre changes the Hamiltonian to
Importantly, the flux Φ affects only the extended states. It does not change the localised states. To see this, we attempt to undo the flux by a gauge transformation,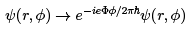
For the localised states, where 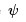 is non-zero only in some finite region, there’s no problem in doing this. However for the extended states, which wrap around the annulus, we also have the requirement that the wavefunction
is non-zero only in some finite region, there’s no problem in doing this. However for the extended states, which wrap around the annulus, we also have the requirement that the wavefunction  is single-valued as
is single-valued as  We see that this is only true when $ is an integer multiple of
We see that this is only true when $ is an integer multiple of 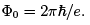 .
.
The upshot of this argument is that the spectrum of the Hamiltonian is again left unchanged when $ is an integer multiple of $0. But, this time, as the flux is increased from 0 to $0, the localised states don’t change. Only the extended states undergo spectral flow; these alone must map onto themselves.
There are always at least two extended states: one near the inner ring and one near the outer ring. The spectral flow happens in the same heuristic manner as described above: an extended state localised at one radius is transformed into an extended state at the next available radius. The presence of disorder means that there are fewer extended states, but this doesn’t change the overall conclusion: if all extended states in a given Landau level are filled, then the net effect of dialling the flux from Φ = 0 to Φ = Φ0 is to transport one electron from the inner to the outer edge. If n Landau levels are filled, we again get the result (2.7).
The arguments above involving gauge transformations start to give a hint of the topological nature of the quantum Hall effect. In fact, there are much deeper topological ideas underlying the quantisation of the Hall conductivity. We’ll describe these in Section 2.2.4 and, in a slightly different context, in Section 2.3. However, before we proceed we first need a basic result which gives an expression for the conductivity in any quantum mechanical system.
|
210 videos|156 docs|94 tests
|
FAQs on The Integer Quantum Hall Effect (Part-2) - Basic Physics for IIT JAM
| 1. What is the Integer Quantum Hall Effect? |  |
| 2. How does the Integer Quantum Hall Effect occur? |  |
| 3. What are the applications of the Integer Quantum Hall Effect? |  |
| 4. Can the Integer Quantum Hall Effect be observed at room temperature? |  |
| 5. How does the Integer Quantum Hall Effect differ from the Fractional Quantum Hall Effect? |  |

|
Explore Courses for Physics exam
|

|

















