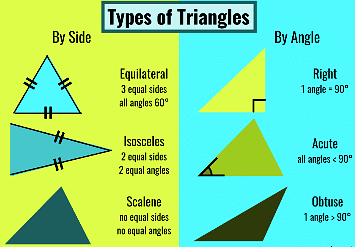
The Triangle and its Properties - 1 | Mathematics for JSS 2 PDF Download
What is Triangle?
A triangle, you have seen, is a simple closed curve made of three line segments. It has three vertices, three sides, and three angles.
You know how to classify triangles based on the (i) sides (ii) angles.
(i) Based on Sides: Scalene, Isosceles, and Equilateral triangles.
(ii) Based on Angles: Acute-angled, Obtuse-angled, and Right-angled triangles.
1. Triangles based on their side
- Equilateral triangle: A triangle in which all the sides are equal is called an Equilateral triangle. All three angles of an equilateral triangle are also equal, and each measures 60°.
- Isosceles triangle: A triangle in which any two sides are equal is called an Isosceles triangle. In an isosceles triangle, the angles opposite the equal sides are called the base angles, and they are equal.
- Scalene triangle: A triangle in which no two sides are equal is called a Scalene triangle.
 Types of Triangle
Types of Triangle 2. Triangles based on their angles
- Acute-angled triangle: A triangle with all angles less than 90° is known as an Acute-angled triangle.
- Obtuse-angled triangle: A triangle with one of its angles more than 90° and less than 180° is known as an Obtuse-angled triangle.
- Right-angled triangle: A triangle with one of its angles equal to 90° is known as a Right-angled triangle.
The side opposite the 90° angle is called the Hypotenuse and is the Longest side of the triangle.
What is the Median of a Triangle?
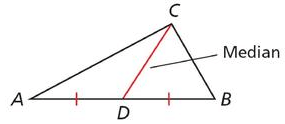 The median of a Triangle
The median of a Triangle
- A median of a triangle is a line segment that joins a vertex to the mid-point of the side that is opposite to that vertex.
- A median connects a vertex of a triangle to the mid-point of the opposite side.
Properties of Median of Triangle
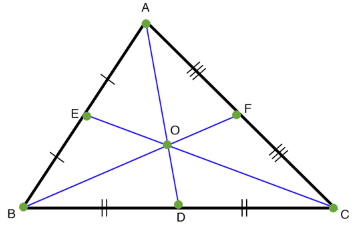
- The median divides the vertex angle in isosceles and equilateral triangles, where the two adjacent sides are equal.
- The centroid is the point where the three medians of a triangle intersect.
- A median splits the triangle's area in half.
- The centroid divides the triangle into six smaller triangles with equal areas.
- In an equilateral triangle, the medians have the same length.
- In an isosceles triangle, medians from vertices with equal angles have the same length.
- In a scalene triangle, the medians have different lengths.
- The sum of two triangle sides is greater than the median drawn from the common vertex.
- There is a relationship between the median and side lengths: "3 times the sum of squares of the side lengths = 4 times the squares of the medians of a triangle."
What is the Altitude of a Triangle?
A triangle's altitude is the vertical distance from the corner to the opposite side of the shape. The height of a triangle also called its altitude, is a straight line drawn from the triangle's vertex to the opposite side, forming a right-angled triangle with the base.
Properties of Altitude of a Triangle
- Every triangle has a maximum of three altitudes.
- These altitudes can be either inside or outside the triangle, depending on the type of triangle.
- The point where the three altitudes intersect is called the Orthocenter, which can also be either inside or outside the triangle.
Position of Altitude in Different Triangles
1. Scalene Triangle: A scalene triangle is one in which all three sides are of different lengths.  Scalene TriangleThe steps to derive the formula are as follows:
Scalene TriangleThe steps to derive the formula are as follows:
- The area of a triangle using Heron's formula is, Area=√s(s−a)(s−b)(s−c).
- The basic formula to find the area of a triangle with respect to its base 'b' and altitude 'h' is:
Area = 1/2 × b × h - If we place both the area formulas equally, we get,12×b×h=√s(s−a)(s−b)(s−c)
- Therefore, the altitude of a scalene triangle is
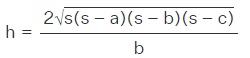 2. Isosceles Triangle: A isosceles triangle in which two sides are equal is called an isosceles triangle. The altitude of an isosceles triangle is perpendicular to its base.
2. Isosceles Triangle: A isosceles triangle in which two sides are equal is called an isosceles triangle. The altitude of an isosceles triangle is perpendicular to its base.
 Isosceles Triangle
Isosceles Triangle
- Let us see the derivation of the formula for the altitude of an isosceles triangle.
- In the isosceles triangle given above, side AB = AC, BC is the base, and AD is the altitude.
- Let us represent AB and AC as 'a, BC as 'b', and AD as 'h'. One of the properties of the altitude of an isosceles triangle is that it is the perpendicular bisector to the base of the triangle.
- So, by applying Pythagoras theorem in △ADB, we get,

3. Equilateral triangle: A triangle in which all three sides are equal is called an equilateral triangle.
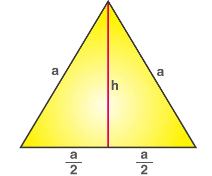 Equilateral Triangle
Equilateral Triangle
Let us assume, the sides of the equilateral triangle to be 'a', its perimeter = 3a. Therefore, its semi-perimeter (s) = 3a/2 and the base of the triangle (b) = a.
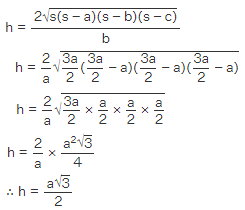
4. Right Triangle: In a right triangle, one angle measures 90 degrees.
In this case, one altitude is the same as the side opposite the right angle (the hypotenuse), and the other two altitudes are the legs of the triangle. The orthocenter is at the right angle vertex.
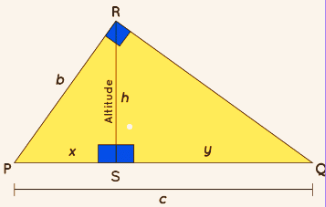 Right Triangle
Right Triangle
In the above figure, Let us see the derivation of the formula for the altitude of a right triangle.
△PSR ∼△RSQ

5. Obtuse Triangle: In an obtuse triangle, one angle measures more than 90 degrees.
In this case, one altitude lies outside the triangle, and the other two altitudes lie inside the triangle. The orthocenter is located outside the triangle.
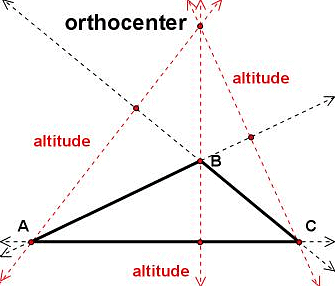 Obtuse Triangle
Obtuse Triangle
Important Formulas
| Equilateral Triangle | h = (½) × √3 × s |
| Isosceles Triangle | h =√(a2−b2/4) |
| Right Triangle | h =√(xy) |
What are the Differences between Median and Altitude?

What is the Exterior Angle of a Triangle and Its Property?
An exterior angle of a triangle is equal to the sum of its interior opposite angles.
To prove:
∠ACD = ∠A + ∠B
 Exterior Angle of a Triangle
Exterior Angle of a Triangle
We will prove this using the alternate angles property.
Let's draw a line CE from C which is parallel to AB.
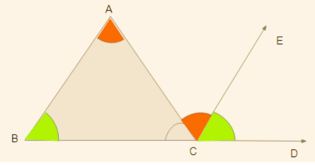 The exterior Angle of a Triangle shows the line CE II AB
The exterior Angle of a Triangle shows the line CE II AB
Note: It is obvious that the exterior angle of a triangle is equal to the sum of its opposite interior angles.
Properties of Exterior Angles of a Triangle
- The sum of the opposite internal angles of a triangle equals the triangle’s exterior angle.
- In all circumstances, if an equivalent angle is taken at each vertex of the triangle, the exterior angles sum up to 360°. Indeed, this statement applies to any convex polygon, not only triangles.
- According to the external angle theorem, the measure of an exterior angle is equal to the sum of the two distant interior angles of a triangle.
- According to the external angle inequality theorem, the measure of any exterior angle of a triangle is greater than either of the opposite interior angles.
- The adjacent interior angle and the exterior angle are supplementary. The total of a triangle’s outer angles is 360°.
What is the Angle Sum Property of a Triangle?
A triangle is the smallest polygon that has three sides and three interior angles.
Theorem: The angle sum property of triangle states that the sum of interior angles of a triangle is 180°.
Proof: Consider an ∆ABC, as shown in the figure below.
Draw a line PQ parallel to the side BC of the given triangle.
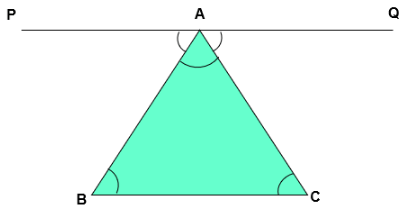 Angle Sum Property of a TriangleSo, PQ is a straight line, it can be concluded that:
Angle Sum Property of a TriangleSo, PQ is a straight line, it can be concluded that:
∠PAB + ∠BAC + ∠QAC = 180° ..(1)
Since PQ||BC and AB, AC are transversals,
Therefore,
∠QAC = ∠ACB (a pair of alternate angles)
Also, ∠PAB = ∠CBA (a pair of alternate angles)
Substituting the value of ∠QAC and ∠PAB in equation (1),
∠ACB + ∠BAC + ∠CBA= 180°
Note: The sum of the interior angles of a triangle is 180°.
Two Special Triangles: Equilateral and Isosceles
1. Equilateral Triangle
An equilateral triangle is one in which all three sides are equal. It is a special case of the isosceles triangle where the third side is also equal. In the triangle XYZ, XY = YZ = ZX.
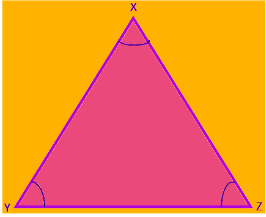 Equilateral Triangle
Equilateral Triangle
The properties of an equilateral triangle are:
- It has 3 equal sides.
- It has 3 equal angles.
- Since the sum of the interior angles is 180 degrees, every angle of an equilateral triangle is 60 degrees.
- It is a regular polygon with 3 sides.
- The altitude and median from a vertex are the same single line.
- The ortho-center and centroid of the triangle are at the same point.
2. Isosceles Triangle
An isosceles triangle is a triangle that comprises 2 equal sides, regardless of the direction of the apex of the triangle points.
 Isosceles Triangle In the isosceles triangle ABC, AB = AC.
Isosceles Triangle In the isosceles triangle ABC, AB = AC.
Some of its properties are:
- It has two equal sides.
- It has two equal angles, that is, the base angles.
- When the third angle is 90 degrees, it is called a right isosceles triangle.
- The altitude from the apex to the base bisects the angle at the apex.
What is the Sum of the Lengths of Two Sides of a Triangle?
According to this principle, the sum of the lengths of any two sides of a triangle must be greater than the length of the third side. This rule is known as the Triangle Inequality Theorem.
Mark three non-collinear spots A, B, and C in your playground ΔABC
ΔABC
Now, start from A and reach C, walking along one or more of these paths.
She can, for example, walk first along AB and then along BC to reach C, or she can walk straight along AC.
She will naturally prefer the direct path AC. If she takes the other path (AB and then BC ), she will have to walk more.
In other words,
(i) AB + BC > AC
Similarly, if one were to start from B and go to A, he or she will not take the route BC and CA but will prefer BA This is because
(ii) BC + CA > AB
By a similar argument, you find that
(iii) CA + AB > BC
Note: This observation suggests that the sum of the lengths of any two sides of a triangle is greater than the third side.
Right-Angled Triangles and Pythagoras Property
Pythagoras, a Greek philosopher of the sixth century B.C. is said to have found a very important and useful property of right-angled triangles.
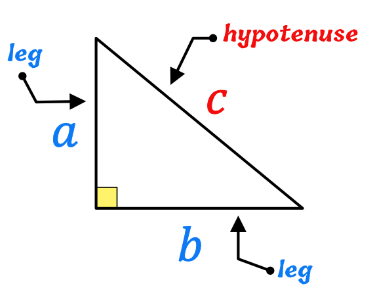 Pythagorean Theorem
Pythagorean Theorem
Note: In a right-angled triangle, the sides have some special names. The side opposite to the right angle is called the hypotenuse; the other two sides are known as the legs of the right-angled triangle.
Pythagorean Theorem Statement
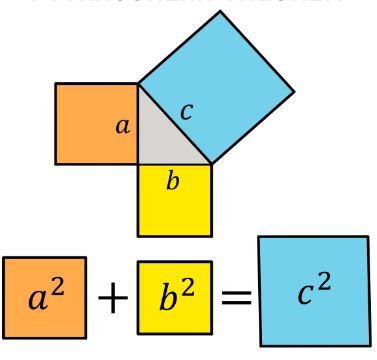 Pythagorean Theorem Formula Pythagoras' theorem states that “In a right-angled triangle, the square of the hypotenuse side is equal to the sum of squares of the other two sides“. The sides of this triangle have been named Perpendicular, Base, and Hypotenuse.
Pythagorean Theorem Formula Pythagoras' theorem states that “In a right-angled triangle, the square of the hypotenuse side is equal to the sum of squares of the other two sides“. The sides of this triangle have been named Perpendicular, Base, and Hypotenuse.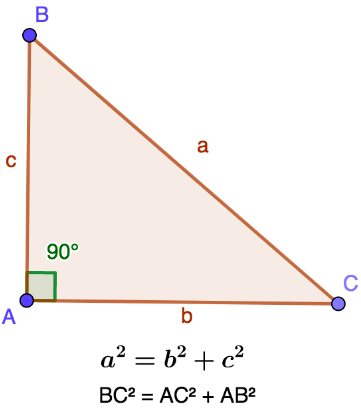 Pythagoras Theorem
Pythagoras Theorem
Derivation of Pythagorean Theorem Formula
Consider a right-angled triangle ABC, right-angled at B. Draw a perpendicular BD meeting AC at D.
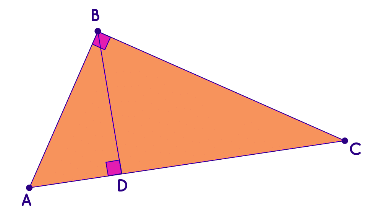 Right Angled Triangle
Right Angled Triangle
In △ABD and △ACB,
∠A = ∠A (common)
∠ADB = ∠ABC (both are right angles)
Thus, △ABD ∼ △ACB (by AA similarity criterion)
Similarly, we can prove △BCD ∼ △ACB.
Thus △ABD ∼ △ACB,
Therefore, AD/AB = AB/AC.
We can say that AD × AC = AB2.
Similarly, △BCD ∼ △ACB.
Therefore, CD/BC = BC/AC. We can also say that CD × AC = BC2.
Adding these 2 equations,
we get AB2 + BC2 = (AD × AC) + (CD × AC)
AB2 + BC2 = AC(AD +DC)
AB2 + BC2 =AC2
Hence proved.
Example: Consider a right-angled triangle with sides of lengths 5, 12, and c units. We can check if the Pythagorean theorem holds true for this triangle:
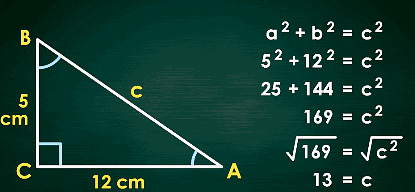 Example of Pythagorean Theorem
Example of Pythagorean Theorem
Note:
- Since both the values are equal, the Pythagorean theorem holds true for this right-angled triangle.
- This theorem is an essential concept in mathematics and can be used to solve various problems involving right-angled triangles.
|
83 videos|156 docs|32 tests
|
FAQs on The Triangle and its Properties - 1 - Mathematics for JSS 2
| 1. What is a triangle? |  |
| 2. What is the median of a triangle? |  |
| 3. What is the altitude of a triangle? |  |
| 4. What are the differences between median and altitude? |  |
| 5. What is the angle sum property of a triangle? |  |

|
Explore Courses for JSS 2 exam
|

|