The distance of Point From a Line | Mathematics (Maths) Class 11 - Commerce PDF Download
Distance Between Two Points
We are familiar with the representation of points on a graph sheet. In coordinate geometry, we learned to find the distance between two points, say A and B. Suppose the coordinates of two points are A(x1, y1) and B(x2, y2) lying on the same line. The length or the distance between the two is ((x2 − x1)2 + (y2 − y1)2)1/2 .
Also, we know the area of a triangle formed by three points is given by ½ |x1(y2 − y3) + x2(y3 − y1) + x3(y1 − y2)|. Let us study the way to find the distance of point from a line.
Perpendicular Distance of Point from a Line
Suppose a line l in XY−plane and N(x1, y1) is any point at a distance d from the line l. This line is represented by Ax +By + C = 0. The distance of point from a line, ‘d’ is the length of the perpendicular drawn from N to l. The x and y-intercepts are −C/A and −C/B respectively.
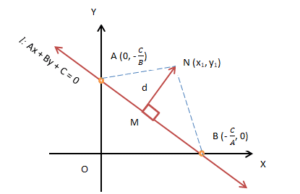
The line meets the y and the x-axes at points A and B respectively. The coordinates of the points are A (0, −C/B) and B (−C/A, 0). The area of the triangle is given byarea (Δ NAB) = ½ base × height = ½ AB × NM,
⇒ NM = 2 area (Δ NAB) / AB … (I)
Also, area (Δ NAB) = ½ |x1(y2 − y3) + x2(y3 − y1) + x3(y1 − y2)|
Or, ½ | x1 (0 + C/B) + (−C/A) (−C/B − y1) +0 (y1 − 0)| = ½ |x1 C/B + y1 C/A + C2/AB|
Or, ½ |C/ (AB) |.|Ax1 + By1 + C|… (II)
Distance of the line AB = ((0 + C/A)2 + (C/B − 0)2)½ = |C| × ((1/A2) + (1/B2))½
Or, Distance, AB = |C/AB| (A2 + B2)½ … (III)
Putting (II) & (III) in (I), we have
NM = d = |Ax1 + By1 + C | / (A2 + B2)½.
It is interesting to find out the distance between two parallel lines.
Distance between Two Parallel Lines
Two lines are parallel to each other if the distance between them at any point remains the same. In other words, if the slopes of both the lines are the same, they will be parallel to each other. Suppose there are two parallel lines l1 and l2 in XY-plane with equal slope = m. The equations of the parallel lines:
y = mx + c1 … (I)
y = mx + c2 … (II)

The distance between two parallel lines is calculated by the distance of point from a line. It is equal to the length of the perpendicular distance from any point to one of the lines. Let N be the point through which the perpendicular or normal is drawn to l1 from M (− c2/m, 0). We know that the distance between two lines is:
d =|Ax1 + By1 + C | / (A2 + B2)½.
Here, A = m, B = 1 and C = c1 (comparing y = mx + c1 and Ax + By + C = 0)
And, x1 = − c2/m and y1 = 0
So, d = |m(− c2/m) + 0 + c1| / (m2 + 1)½ = |c1 − c2| / (m2 + 1)½
Generalizing the above, we have, d =|C1 − C2| / (A2 + B2)½
(If l1: Ax + By + C1 = 0 and l2: Ax + By + C2 = 0)
Solved Example
Problem: Find the distance between two lines 5x + 3y + 6 = 0 and 5x + 3y – 6 = 0.
Solution: Here, A = 5, B = 3, C1 = 6 and C2 = −6. The required distance between the two lines is,
d = |C1 – C2| / (A2 + B2)½ = |6 − (−6)| / (52 + 32)½ = 12/√34.
Problem: Find the distance between the line x/5 + y/2 + 1 = 0 and a point (2, 3).
Solution: The equation of the line can be written as 2x + 5y + 10 = 0. Here, A = 2, B = 5, C = 10, x1 = 2, y1 = 3. The required distance of the point from the line isd =|Ax1 + By1 + C | / (A2 + B2)½ = |2.2 + 5.3 + 10| / (22 + 52)½ = |4 + 15 + 10| /√29 = √29.
|
73 videos|264 docs|91 tests
|
FAQs on The distance of Point From a Line - Mathematics (Maths) Class 11 - Commerce
| 1. What is the formula to find the distance between a point and a line? |  |
| 2. How do I find the equation of a line given a point and its distance from the line? |  |
| 3. Can the distance between a point and a line be negative? |  |
| 4. How is the distance between a point and a line related to perpendicularity? |  |
| 5. Is there a way to find the distance between a point and a line without using a formula? |  |
















