The principle of virtual work | Basic Physics for IIT JAM PDF Download

A special class of problems in mechanics involves systems in equilibrium. The problem is to find the configuration of the system, subject to whatever constraints there may be, when all forces are balanced. The body or system will be at rest (in the inertial rest frame of its centre of mass), meaning that it occupies one point in configuration space for all time. The problem is to find that point. One criterion for finding that point, which makes use of the calculus of variations, is called the principle of virtual work.
According to the principle of virtual work, any infinitesimal virtual displacement in configuration space, consistent with the constraints, requires no work. A virtual displacement means an instantaneous change in coordinates (a real displacement would require finite time during which particles might move and forces might change). To express the principle, label the generalized coordinates r₁, r₂, . . ., r_i, . . . . Then if F_i is the net component of generalized force acting along the coordinate r_i,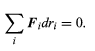
  (93)

Here, F_i dr_i is the work done when the generalized coordinate is changed by the infinitesimal amount dr_i. If r_i is a real coordinate (say, the x coordinate of a particle), then F_i is a real force. If r_i is a generalized coordinate (say, an angular displacement of a rigid body), then F_i is the generalized force such that F_i dr_i is the work done (for an angular displacement, F_i is a component of torque).
Take two simple examples to illustrate the principle. First consider two particles that are restricted to motion in the x direction and are constrained by a taut string connecting them. If their x coordinates are called x₁ and x₂, then F₁dx₁ + F₂dx₂ = 0 according to the principle of virtual work. But the taut string requires that the particles be displaced the same amount, so that dx₁= dx₂, with the result that F₁ + F₂ = 0. The particles might be in equilibrium, for example, under equal and opposite forces, but F₁ and F₂ do not need individually to be zero. This is generally true of the F_i in equation. As a second example, consider a rigid body in space. Here, the constraint of rigidity has already been expressed by reducing the coordinate space to that of six generalized coordinates. These six coordinates (x, y, z, and three angles) can change quite independently of one another. In other words, in equation, the six dr_i are arbitrary. Thus, the only way equation can be satisfied is if all six F_i are zero. This means that the rigid body can have no net component of force and no net component of torque acting on it. Of course, this same conclusion was reached earlier (see Statics) by less abstract arguments.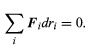
  (93)