Thermal Stresses | Strength of Materials (SOM) - Mechanical Engineering PDF Download
| Table of contents |

|
| What is Thermal Stress? |

|
| Thermal Stress and Strain |

|
| Thermal Stress in Varying Cross-Section |

|
| Thermal Stress in Composite Bars |

|
| Solved Numericals |

|
What is Thermal Stress?
Thermal stress is the stress developed in a body due to a change in temperature. This type of stress arises when there is a temperature change (either a rise or a drop), and the body is constrained from expanding or contracting freely.Causes of Thermal Stress
Thermal stress occurs under the following conditions:
- Temperature Rise: When the temperature of a body increases, it tends to expand. If the expansion is restricted, compressive thermal stress develops.
- Temperature Drop: When the temperature of a body decreases, it tends to contract. If the contraction is restricted, tensile thermal stress develops.
Suppose a bar that is free to expand. Consider the below figure; assume the cross-sectional area A, length of bar L, and coefficient of thermal expansion is ‘α’.
‘t’ is the change in temperature
Δ is the free thermal expansion Free thermal expansion for the above case is given by
Free thermal expansion for the above case is given by
Δ = Lαt
If the temperature is reducing then there will be a contraction given by
Δ = Lαt
In this particular condition, no thermal stress is developed as there is no restriction for expansion or contraction. Stress is developed only when there is restriction or resistance to free motion.
Thermal Stress and Strain
As we know, thermal stress is the stress induced in a body due to a change in temperature. Due to this development of thermal stress, thermal strain is induced in that body. It can be said that thermal stress and strains are developed in the body when it is heated or cooled. Generally, a thermal strain developed due to thermal stress is very small. As the material will expand or contract in all directions, the thermal strain will be developed in all directions.Thermal Stress in Simple Bars
Case 1: When boundaries are fixed– Consider Figure A, as there is no restriction for expansion or contraction when there is a change in temperature, the thermal stress developed is zero and the free expansion is Lαt. Also Consider Figure B, as both ends are fixed, free movement is not possible when there is a change in temperature, this leads to the development of thermal stress in the body.
Deformation due to force PT = PTL/AE
Deformation due to force PT = ∆
PTL/AE = Lαt
σT = αtE
where σT = Thermal Stress
σT is compressive stress when there is an increase in temperature because when there is a temperature rise, the body tries to expand but boundaries will try to keep it in its original position, so the thermal forces will be compressive.
σT is tensile when there is a decrease in temperature because when there is a temperature drop, the body tries to contract, but the boundaries will try to keep it in its original position, so the thermal forces will be tensile.
Case 2: Thermal Stress when Support Yield
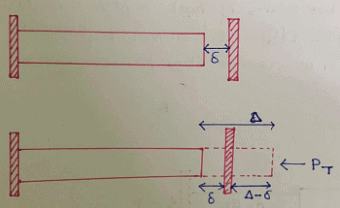
Free Expansion = Lαt
Net Deformation = Δ – δ (where δ is the support yield or gap)
Net Deformation = Lαt – δ
Deformation due to force PT= PTL/AE
Deformation due to force PT = Net Deformation
Lαt – δ= PTL/AE
Lαt – δ= σTL/E
Thermal Stress in Varying Cross-Section
Consider a series of bars that have different cross-section areas and different lengths, different materials, to find the stress in different bars. Let us assume that the temperature is increasing. When there is an increase in temperature, the bars will try to expand, but the boundaries will restrict the expansion by exerting force (P).
The force in both bars is the same.
(Force)1 = (Force)2
σ1A1= σ2A2
σ1= σ2A2A1
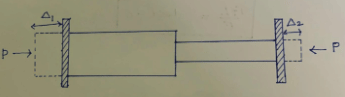
Free Expansion = Δ = Δ1 + Δ2
= L1α1t + L2α2t
Deformation due to force P = PL1/A1E1 + PL2/A2E2
Deformation in bars due to P = Free Expansion
PL1/A1E1 + PL2/A2E2 = L1α1t + L2α2t
σ1L1/E1 + σ2L2/E2 = (L1α1 + L2α2)t
Thermal Stress in Composite Bars

Composite bars are the bars in which there will be bars of different materials whose coefficient of thermal expansion is different and are clubbed together so that they act as a single unit and there will be the same explanation in both bars. As both bars act as a single unit, the deformation in both bars will be the same. Thermal stress in composite bars can be given by the following formula:-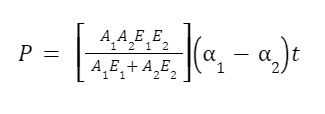
Solved Numericals
Q1. A steel rod with a cross-sectional area of 0.25 in2 is stretched between two fixed points. The tensile load at 70°F is 1200 lb. What will be the stress at 0°F? At what temperature will the stress be zero? Assume α = 6.5 × 10-6 in / (in·°F) and E = 29 × 106 psi.
Solution: For the stress at 0°C: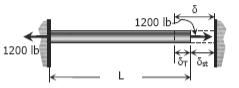
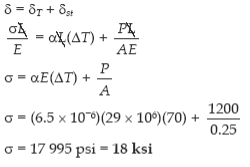
For the temperature that causes zero stress:
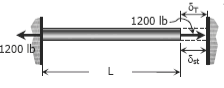
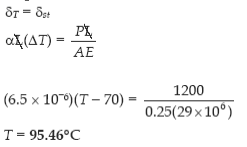
Q2. A steel rod is stretched between two rigid walls and carries a tensile load of 5000 N at 20°C. If the allowable stress is not to exceed 130 MPa at -20°C, what is the minimum diameter of the rod? Assume α = 11.7 µm/(m·°C) and E = 200 GPa.
Solution: 
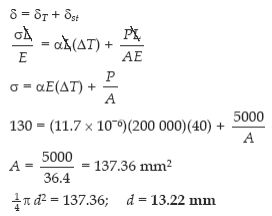
Q3. Steel railroad reels 10 m long are laid with a clearance of 3 mm at a temperature of 5°C. At what temperature will the rails just touch? What stress would be induced in the rails at that temperature if there were no initial clearance? Assume α = 11.7 µm/(m·°C) and E = 200 GPa.
Solution: 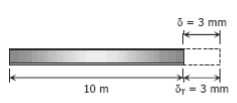

Required stress:
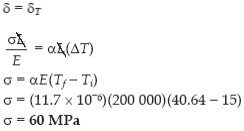
|
37 videos|39 docs|45 tests
|
FAQs on Thermal Stresses - Strength of Materials (SOM) - Mechanical Engineering
| 1. What is thermal stress and how does it differ from mechanical stress? |  |
| 2. How does thermal stress affect materials with varying cross-sections? |  |
| 3. What are the factors that influence thermal stress in composite bars? |  |
| 4. How can thermal stresses be minimized or controlled in structures? |  |
| 5. Why is it important to consider thermal stress in engineering design? |  |

|
Explore Courses for Mechanical Engineering exam
|

|
















