All Courses
Get the App Signup / Login
Sign in Open App
Physics Exam  >  Physics Notes  >  Physics for IIT JAM, UGC - NET, CSIR NET  >  Thermodynamic Potentials - Thermodynamic and Statistical Physics

Thermodynamic Potentials - Thermodynamic and Statistical Physics | Physics for IIT JAM, UGC - NET, CSIR NET PDF Download

Introduction

  • Thermodynamic potentials are important functions in statistical mechanics that connect the behavior of tiny particles to the overall properties of larger systems. 
  •  These potentials help us find various thermodynamic quantities and allow us to predict how systems will act under different conditions. 
  • The main types of thermodynamic potentials include: 
    • Internal energy
    • Enthalpy
    • Helmholtz free energy
    • Gibbs free energy
  •  Each potential has its own natural variablesand uses, such as: 
    • Finding equilibrium conditions
    • Predicting spontaneous processes
    • Understanding phase transitions

Internal Energy

  • The total energy in a thermodynamic system is represented as U.
  • This energy includes the kinetic and potential energies of all the particles within the system.
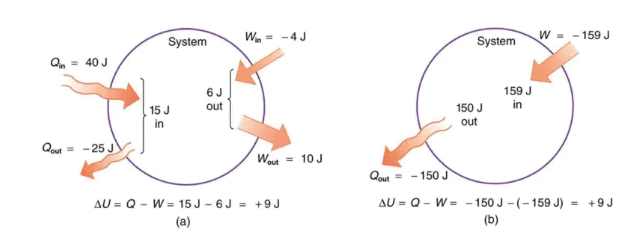
  • U is essential for understanding the First Law of Thermodynamics, which is expressed as: dU = δQ - δWThermodynamic Potentials - Thermodynamic and Statistical Physics | Physics for IIT JAM, UGC - NET, CSIR NET
  • The energy U depends on certain extensive properties, such as:
    • Entropy
    • Volume
    • Number of particles
  • The natural variablesthat relate to this energy are:
    • Entropy (S)
    • Volume (V)

Enthalpy

  • H = U + PV, where P represents pressure and V stands for volume.
  • It measures the total heat content of a system.
  • This concept is especially useful for processes that happen at constant pressure, known as isobaric processes.
  • Changes in enthalpy (ΔH) show the heat that is either absorbed or released during chemical reactions.
  • Two important variables related to enthalpy are entropy (S) and pressure (P).

Helmholtz free energy

  • A is expressed as A = U - TS, where T stands for temperature and S means entropy.
  • This equation shows the useful work that can be obtained from a closed system when the temperature is constant.
  • The value of A is at its lowest point when the system is in equilibrium, especially in situations with a fixed temperature and volume.
  • The equation helps in figuring out the direction of spontaneous processes under conditions of constant temperature and constant volume.
  • The natural variables in this context are temperature (T) and volume (V).

Gibbs free energy

  • G is defined as G = H - TS or G = U + PV - TS
  • G measures the maximum work that can be obtained from a system in a reversible way.
  • G is at its lowest point when a system is in equilibrium at constant temperature and pressure.
  • It is important for understanding chemical equilibrium and whether reactions will occur spontaneously.
  • The key variables that affect G are temperature (T) and pressure (P).

Mathematical formulations

Legendre transformations

  • Mathematical method used to change between different thermodynamic potentials.
  • Facilitates the conversion between conjugate variables, which include both extensive and intensive properties.
  • Maintains the information content while altering the independent variables.
  • General formula:
  • F(x,y) = f(x,y) - y ∂f/∂y
  • This method allows for the derivation of new potentials from existing ones, such as transforming U (internal energy) to H (enthalpy) and A (Helmholtz free energy) to G (Gibbs free energy).

Partial derivatives relationships

  • Connecting Thermodynamic Quantities: Various thermodynamic properties can be linked through mathematical equations. 
  • Fundamental Equation:
    • dU: This represents the change in internal energy. 
    • T: This is the temperature. 
    • dS: This indicates the change in entropy. 
    • P: This refers to pressure. 
    • dV: This signifies the change in volume. 
    • dN: This denotes the change in the number of particles. 
    • The fundamental equation can be expressed as: dU = TdS - PdV + μdN
  • Derived Relationships:
    • (∂U/∂S)V,N = T
    • (∂U/∂V)S,N = -P
    • (∂U/∂N)S,V = μ

Calculating Quantities: These equations allow for the calculation of one thermodynamic quantity based on measurements of other quantities.

Maxwell Relations

F = F ( x , y ) and if it is perfect differential then d F = M dx + NdyThermodynamic Potentials - Thermodynamic and Statistical Physics | Physics for IIT JAM, UGC - NET, CSIR NETthen, M and N will satisfy the condition Thermodynamic Potentials - Thermodynamic and Statistical Physics | Physics for IIT JAM, UGC - NET, CSIR NETMaxwell relations are relationship between two derivatives of thermodynamic variables, and energy due to the equivalence of potential second derivative under a change of operation order
Thermodynamic Potentials - Thermodynamic and Statistical Physics | Physics for IIT JAM, UGC - NET, CSIR NETWhere F is thermodynamic potential and x and y are two of its natural independent variables.

Maxwell relations are extremely important for two reasons: 
(i) First they show us that derivative of thermodynamic parameters are not all independent. This can serve as a consistency check in both experiments and in theoretical analysis.
(ii) Maxwell relations provide a method for expressing some derivative in other ways. This enables as to connect difficult to measure quantities to those which are readily accessible experimentally.
The measurement of entropy and chemical potential can not be directly measurable in lab but with the help of Maxwell relation there thermodynamic property can be determine theoretically.
For Maxwell relation,

Let us Legendre the independent variable as x , and y such that
U = U(x,y), S = S(x, y) V = V(x, y)
So Thermodynamic Potentials - Thermodynamic and Statistical Physics | Physics for IIT JAM, UGC - NET, CSIR NETThermodynamic Potentials - Thermodynamic and Statistical Physics | Physics for IIT JAM, UGC - NET, CSIR NETFrom first law of thermodynamic
dU = TdS - PdV
Thermodynamic Potentials - Thermodynamic and Statistical Physics | Physics for IIT JAM, UGC - NET, CSIR NETHence U,V, and S are perfect differential.
Then
Thermodynamic Potentials - Thermodynamic and Statistical Physics | Physics for IIT JAM, UGC - NET, CSIR NETThermodynamic Potentials - Thermodynamic and Statistical Physics | Physics for IIT JAM, UGC - NET, CSIR NET

Thermodynamic Potentials - Thermodynamic and Statistical Physics | Physics for IIT JAM, UGC - NET, CSIR NET

SimilarlyThermodynamic Potentials - Thermodynamic and Statistical Physics | Physics for IIT JAM, UGC - NET, CSIR NET
Equating equation (1) and (2)
Thermodynamic Potentials - Thermodynamic and Statistical Physics | Physics for IIT JAM, UGC - NET, CSIR NET

Maxwell first relation:-  put x = T , y = V
Thermodynamic Potentials - Thermodynamic and Statistical Physics | Physics for IIT JAM, UGC - NET, CSIR NET

Maxwell Second Relation:-  put x = T ,y = P
Thermodynamic Potentials - Thermodynamic and Statistical Physics | Physics for IIT JAM, UGC - NET, CSIR NETMaxwell Third Relation:- put x = s , y = vThermodynamic Potentials - Thermodynamic and Statistical Physics | Physics for IIT JAM, UGC - NET, CSIR NET

Maxwell Fourth Relation:- put x = S, y = P
Thermodynamic Potentials - Thermodynamic and Statistical Physics | Physics for IIT JAM, UGC - NET, CSIR NET

Thermodynamic potential is a scalar function used to represent the thermodynamic state of system. The concept of thermodynamic potentials was introduced by Pierre Duhem in 1886.

One main thermodynamic potential that has a physical interpretation is the internal energy.

It is energy of configuration of a given system of conservative forces. Expression for all other thermodynamic energy potentials are drivable via Legendre transformation.

Different Types of Thermodynamic Potential and Maxwell Relation

Thermodynamic potentials are different form of energy which can be used in different thermodynamic process. Thermodynamic potentials are path independent variables so they are perfect differential.
If F is unique thermodynamic potential defined by variables x and y as F = F ( x , y ) and if it is perfect differential then dF = Mdx + Ndy
Thermodynamic Potentials - Thermodynamic and Statistical Physics | Physics for IIT JAM, UGC - NET, CSIR NETthen M and N will satisfy the condition

Thermodynamic Potentials - Thermodynamic and Statistical Physics | Physics for IIT JAM, UGC - NET, CSIR NET

Internal Energy
U and second from the first laws of thermodynamics 
dU = TdS - PdV
from Legendre transformation
Thermodynamic Potentials - Thermodynamic and Statistical Physics | Physics for IIT JAM, UGC - NET, CSIR NETfrom given relation one can derive Maxwell relationThermodynamic Potentials - Thermodynamic and Statistical Physics | Physics for IIT JAM, UGC - NET, CSIR NET
Enthalpy
(H) the enthalpy is defined as H = U + PV 
dH = dU + PdV + VdP 
from Laws of thermodynamics,
 TdS = dU + PdV 
& dH = TdS + VdP 
from Legendre transformation
Thermodynamic Potentials - Thermodynamic and Statistical Physics | Physics for IIT JAM, UGC - NET, CSIR NET
The Enthalpy H is Extensive quantity, which can not be measured directly. Thus change in enthalpy is more useful.
△H is positive in endothermic reaction and negative in exothermic reaction.
From above relation one can derive Maxwell relation Thermodynamic Potentials - Thermodynamic and Statistical Physics | Physics for IIT JAM, UGC - NET, CSIR NET
△H of a system is equal to sum of non-mechanical work done on it and the heat supplied to it.
Helmholtz Free Energy
(F) the Helmholtz free energy is defined F = U - T S
 dF = dU - TdS - SdT 
From laws of thermodynamics, d U = T d S - P d V 
dF = TdS - PdV - TdS - SdT 
dF = - P d V - SdT
 From Legendre transformation
Thermodynamic Potentials - Thermodynamic and Statistical Physics | Physics for IIT JAM, UGC - NET, CSIR NET
From above relation one can derive Maxwell relationThermodynamic Potentials - Thermodynamic and Statistical Physics | Physics for IIT JAM, UGC - NET, CSIR NET
The free Energy F, which is available energy for work in reversible isothermal process.
Gibbs Energy: ‘G’ is defined as G = H - TS .
G = U + P V - T S
dG = dU + PdV - VdP - TdS - SdT 
TdS - PdV + PdV + VdP - TdS - SdT 
dG = VdP - SdT
 from Legendre transformation
Thermodynamic Potentials - Thermodynamic and Statistical Physics | Physics for IIT JAM, UGC - NET, CSIR NET
From above relation one can derive Maxwell relation
Thermodynamic Potentials - Thermodynamic and Statistical Physics | Physics for IIT JAM, UGC - NET, CSIR NET
Gibbs free energy is popularly as free enthalpy.
  • The Gibbs free energy is Maximum amount of nonexpanding work that can be exacted from a closed system.
  • The maximum will activated when the system is in reversible process.
  • Gibbs free energy is also treated as chemical potential.
  • In thermodynamics, chemical potential, as partial molar free energy, is a form of potential energy that can be absorbed or relived during a chemical reaction.
  • The chemical potential of a species in the minute can be defined the slope of the energy at system with respect to a change in the no of moles.Thermodynamic Potentials - Thermodynamic and Statistical Physics | Physics for IIT JAM, UGC - NET, CSIR NET

where Thermodynamic Potentials - Thermodynamic and Statistical Physics | Physics for IIT JAM, UGC - NET, CSIR NET is chemical potential, G is Gibbs energy and N is no of molecules

Example 1: Prove that internal energy U is given by
Thermodynamic Potentials - Thermodynamic and Statistical Physics | Physics for IIT JAM, UGC - NET, CSIR NETSolution: (a) F = U-TS =U = F + TSThermodynamic Potentials - Thermodynamic and Statistical Physics | Physics for IIT JAM, UGC - NET, CSIR NETThermodynamic Potentials - Thermodynamic and Statistical Physics | Physics for IIT JAM, UGC - NET, CSIR NETG = H-TS

Thermodynamic Potentials - Thermodynamic and Statistical Physics | Physics for IIT JAM, UGC - NET, CSIR NETApplication of Maxwell Relation

  • First T - dS equation
    Let T, and \/are independent variable S = S (T, V)

Thermodynamic Potentials - Thermodynamic and Statistical Physics | Physics for IIT JAM, UGC - NET, CSIR NET

  • Second T - dS Equation
    Let T and P are independent variable S = S(T, P).

Thermodynamic Potentials - Thermodynamic and Statistical Physics | Physics for IIT JAM, UGC - NET, CSIR NETFrom Maxwell relation

  • Thermodynamic Potentials - Thermodynamic and Statistical Physics | Physics for IIT JAM, UGC - NET, CSIR NETThird T-dS Equation

Let P , V are independent variable S = S (P ,V )

Thermodynamic Potentials - Thermodynamic and Statistical Physics | Physics for IIT JAM, UGC - NET, CSIR NET

Thermodynamic Potentials - Thermodynamic and Statistical Physics | Physics for IIT JAM, UGC - NET, CSIR NET

The First Energy Equation
Let T and V are independent variable U = U(T, V)

Thermodynamic Potentials - Thermodynamic and Statistical Physics | Physics for IIT JAM, UGC - NET, CSIR NETFrom first law of thermodynamics,
dU = TdS - PdV

Thermodynamic Potentials - Thermodynamic and Statistical Physics | Physics for IIT JAM, UGC - NET, CSIR NETUsing Maxwell relationThermodynamic Potentials - Thermodynamic and Statistical Physics | Physics for IIT JAM, UGC - NET, CSIR NETThermodynamic Potentials - Thermodynamic and Statistical Physics | Physics for IIT JAM, UGC - NET, CSIR NET

Second Energy Equation

Thermodynamic Potentials - Thermodynamic and Statistical Physics | Physics for IIT JAM, UGC - NET, CSIR NET

Using Maxwell relation,Thermodynamic Potentials - Thermodynamic and Statistical Physics | Physics for IIT JAM, UGC - NET, CSIR NETThis is popularly known as second energy equation.

Application of second energy equation

If U is function of independent variable of T and P.

Thermodynamic Potentials - Thermodynamic and Statistical Physics | Physics for IIT JAM, UGC - NET, CSIR NET


Example 2: From relation dU = TdS - P d V
Derive Maxwell relation Thermodynamic Potentials - Thermodynamic and Statistical Physics | Physics for IIT JAM, UGC - NET, CSIR NET 
Solution: dU = TdS - PdVThermodynamic Potentials - Thermodynamic and Statistical Physics | Physics for IIT JAM, UGC - NET, CSIR NETHence U is exact differentialThermodynamic Potentials - Thermodynamic and Statistical Physics | Physics for IIT JAM, UGC - NET, CSIR NET


Example 3: A real gas which obey van der Waal's equation of state are kept in container which has temperature T0 and volume V0. if volume of container changes to V such that temperature of gas become T what is change in entropy?
Solution: Assume Cv is specific heat of constant volume

 For van der Waal's gasThermodynamic Potentials - Thermodynamic and Statistical Physics | Physics for IIT JAM, UGC - NET, CSIR NETFrom first T -dS equationThermodynamic Potentials - Thermodynamic and Statistical Physics | Physics for IIT JAM, UGC - NET, CSIR NETwhere S0 is integration constant.

Some important FAQs are as follows:

Q1. Explain the significance of Legendre transformations in deriving Maxwell relations.

Sol. Legendre transformations allow the redefinition of thermodynamic potentials by replacing natural variables (like S and V) with their conjugates (like T and P). For instance: 
dG = −S dT + V dP
This simplifies the derivation of Maxwell relations and enables the conversion of thermodynamic quantities into measurable forms.

Q2. What is the physical significance of chemical potential (μ) in thermodynamics?

Sol. Chemical potential (μ) represents the change in Gibbs free energy (G) with respect to the number of particles (N):
μ = (∂G / ∂N)T,P
It indicates the potential energy available for particle exchange during chemical reactions and phase transitions.

Q3. A system undergoes a reversible isothermal process. What happens to the Helmholtz free energy (A)?

Sol. During a reversible isothermal process (T = constant), the change in Helmholtz free energy (ΔA) represents the maximum work done by the system:
ΔA = −Wmax
At equilibrium, A is minimized.

Q4. Explain the relationship between enthalpy (H) and entropy (S) during an isobaric process.

Sol. During an isobaric process (P=constant), the change in enthalpy (ΔH) is equal to the heat absorbed or released:
ΔH = TΔS
Here, ΔS is the change in entropy. If ΔH > 0, the process is endothermic; if ΔH < 0, it is exothermic.

Q5. Why is Gibbs free energy important in chemical reactions?

Sol. Gibbs free energy G = H − T S indicates the maximum non-expanding work obtainable from a system at constant temperature and pressure. It predicts:

  • Spontaneity: A reaction is spontaneous if ΔG < 0.
  • Equilibrium: At equilibrium, ΔG = 0.
  • Phase Transitions: Helps determine equilibrium conditions during phase changes.
The document Thermodynamic Potentials - Thermodynamic and Statistical Physics | Physics for IIT JAM, UGC - NET, CSIR NET is a part of the Physics Course Physics for IIT JAM, UGC - NET, CSIR NET.
All you need of Physics at this link: Physics
158 docs
Join Course for Free

Additional FAQs on Thermodynamic Potentials - Thermodynamic and Statistical Physics - Physics for IIT JAM, UGC - NET, CSIR NET

1. What are thermodynamic potentials?
Thermodynamic potentials are mathematical functions that describe the state of a thermodynamic system. They are derived from fundamental thermodynamic principles and provide information about the system's energy, entropy, and other thermodynamic properties.
2. How are thermodynamic potentials related to thermodynamic variables?
Thermodynamic potentials are related to thermodynamic variables through partial derivatives. For example, the internal energy (U) is related to the temperature (T) through the partial derivative dU/dT. Each thermodynamic potential is associated with a specific set of independent variables, and their derivatives provide valuable information about the system's behavior.
3. What is the significance of thermodynamic potentials in studying equilibrium states?
Thermodynamic potentials play a crucial role in studying equilibrium states of a system. Each potential is minimized at equilibrium with respect to its associated independent variables. For instance, the Gibbs free energy (G) is minimized at constant temperature and pressure, making it a useful tool for predicting whether a reaction or process will occur spontaneously.
4. Can you explain the concept of Legendre transformation in relation to thermodynamic potentials?
A Legendre transformation is a mathematical operation that allows us to express a function in terms of its conjugate variables. In the context of thermodynamic potentials, a Legendre transformation is used to convert one potential into another by replacing one independent variable with its conjugate variable. For example, the enthalpy (H) is obtained from the internal energy (U) by a Legendre transformation with respect to volume.
5. How do thermodynamic potentials help in understanding phase transitions?
Thermodynamic potentials provide insights into phase transitions by analyzing the behavior of the system at different values of the potential. For instance, the Helmholtz free energy (F) is useful in studying transitions between different equilibrium states at constant temperature and volume. By examining the behavior of F during phase transitions, we can understand the conditions under which a substance undergoes a phase change.
Related Exams
About this Document
6.3K Views
4.87/5 Rating
Dec 26, 2024 Last updated
Document Description: Thermodynamic Potentials - Thermodynamic and Statistical Physics for Physics 2024 is part of Physics for IIT JAM, UGC - NET, CSIR NET preparation. The notes and questions for Thermodynamic Potentials - Thermodynamic and Statistical Physics have been prepared according to the Physics exam syllabus. Information about Thermodynamic Potentials - Thermodynamic and Statistical Physics covers topics like Introduction, Internal Energy, Enthalpy, Helmholtz free energy, Gibbs free energy, Mathematical formulations, Maxwell Relations, Different Types of Thermodynamic Potential and Maxwell Relation and Thermodynamic Potentials - Thermodynamic and Statistical Physics Example, for Physics 2024 Exam. Find important definitions, questions, notes, meanings, examples, exercises and tests below for Thermodynamic Potentials - Thermodynamic and Statistical Physics.
Introduction of Thermodynamic Potentials - Thermodynamic and Statistical Physics in English is available as part of our Physics for IIT JAM, UGC - NET, CSIR NET for Physics & Thermodynamic Potentials - Thermodynamic and Statistical Physics in Hindi for Physics for IIT JAM, UGC - NET, CSIR NET course. Download more important topics related with notes, lectures and mock test series for Physics Exam by signing up for free. Physics: Thermodynamic Potentials - Thermodynamic and Statistical Physics | Physics for IIT JAM, UGC - NET, CSIR NET
Description
Full syllabus notes, lecture & questions for Thermodynamic Potentials - Thermodynamic and Statistical Physics | Physics for IIT JAM, UGC - NET, CSIR NET - Physics | Plus excerises question with solution to help you revise complete syllabus for Physics for IIT JAM, UGC - NET, CSIR NET | Best notes, free PDF download
Information about Thermodynamic Potentials - Thermodynamic and Statistical Physics
In this doc you can find the meaning of Thermodynamic Potentials - Thermodynamic and Statistical Physics defined & explained in the simplest way possible. Besides explaining types of Thermodynamic Potentials - Thermodynamic and Statistical Physics theory, EduRev gives you an ample number of questions to practice Thermodynamic Potentials - Thermodynamic and Statistical Physics tests, examples and also practice Physics tests
Explore Courses for Physics exam
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.
10M+ students study on EduRev
Related Searches

Previous Year Questions with Solutions

,

study material

,

Objective type Questions

,

CSIR NET

,

practice quizzes

,

past year papers

,

CSIR NET

,

Thermodynamic Potentials - Thermodynamic and Statistical Physics | Physics for IIT JAM

,

mock tests for examination

,

UGC - NET

,

shortcuts and tricks

,

Summary

,

UGC - NET

,

Important questions

,

Extra Questions

,

CSIR NET

,

UGC - NET

,

Exam

,

Free

,

Sample Paper

,

ppt

,

pdf

,

Viva Questions

,

Thermodynamic Potentials - Thermodynamic and Statistical Physics | Physics for IIT JAM

,

Thermodynamic Potentials - Thermodynamic and Statistical Physics | Physics for IIT JAM

,

MCQs

,

Semester Notes

,

video lectures

;
Additional Information about Thermodynamic Potentials - Thermodynamic and Statistical Physics for Physics Preparation

Thermodynamic Potentials - Thermodynamic and Statistical Physics Free PDF Download

The Thermodynamic Potentials - Thermodynamic and Statistical Physics is an invaluable resource that delves deep into the core of the Physics exam. These study notes are curated by experts and cover all the essential topics and concepts, making your preparation more efficient and effective. With the help of these notes, you can grasp complex subjects quickly, revise important points easily, and reinforce your understanding of key concepts. The study notes are presented in a concise and easy-to-understand manner, allowing you to optimize your learning process. Whether you're looking for best-recommended books, sample papers, study material, or toppers' notes, this PDF has got you covered. Download the Thermodynamic Potentials - Thermodynamic and Statistical Physics now and kickstart your journey towards success in the Physics exam.

Importance of Thermodynamic Potentials - Thermodynamic and Statistical Physics

The importance of Thermodynamic Potentials - Thermodynamic and Statistical Physics cannot be overstated, especially for Physics aspirants. This document holds the key to success in the Physics exam. It offers a detailed understanding of the concept, providing invaluable insights into the topic. By knowing the concepts well in advance, students can plan their preparation effectively. Utilize this indispensable guide for a well-rounded preparation and achieve your desired results.

Thermodynamic Potentials - Thermodynamic and Statistical Physics Notes

Thermodynamic Potentials - Thermodynamic and Statistical Physics Notes offer in-depth insights into the specific topic to help you master it with ease. This comprehensive document covers all aspects related to Thermodynamic Potentials - Thermodynamic and Statistical Physics. It includes detailed information about the exam syllabus, recommended books, and study materials for a well-rounded preparation. Practice papers and question papers enable you to assess your progress effectively. Additionally, the paper analysis provides valuable tips for tackling the exam strategically. Access to Toppers' notes gives you an edge in understanding complex concepts. Whether you're a beginner or aiming for advanced proficiency, Thermodynamic Potentials - Thermodynamic and Statistical Physics Notes on EduRev are your ultimate resource for success.

Thermodynamic Potentials - Thermodynamic and Statistical Physics Physics Questions

The "Thermodynamic Potentials - Thermodynamic and Statistical Physics Physics Questions" guide is a valuable resource for all aspiring students preparing for the Physics exam. It focuses on providing a wide range of practice questions to help students gauge their understanding of the exam topics. These questions cover the entire syllabus, ensuring comprehensive preparation. The guide includes previous years' question papers for students to familiarize themselves with the exam's format and difficulty level. Additionally, it offers subject-specific question banks, allowing students to focus on weak areas and improve their performance.

Study Thermodynamic Potentials - Thermodynamic and Statistical Physics on the App

Students of Physics can study Thermodynamic Potentials - Thermodynamic and Statistical Physics alongwith tests & analysis from the EduRev app, which will help them while preparing for their exam. Apart from the Thermodynamic Potentials - Thermodynamic and Statistical Physics, students can also utilize the EduRev App for other study materials such as previous year question papers, syllabus, important questions, etc. The EduRev App will make your learning easier as you can access it from anywhere you want. The content of Thermodynamic Potentials - Thermodynamic and Statistical Physics is prepared as per the latest Physics syllabus.
© EduRev
Education Revolution
Signup to see your scores go up within 7 days!
Access 1000+ FREE Docs, Videos and Tests
Takes less than 10 seconds to signup