Three Dimensional Geometry | The Complete SAT Course - Class 10 PDF Download
3D Geometry is used to represent a point, a line, or a plane with reference to the x-axis, y-axis, and z-axis respectively. The three-dimensional geometry has all the concepts similar to the two-dimensional coordinate geometry.
What is 3D Geometry?
The 3d geometry helps in the representation of a line or a plane in a three-dimensional plane, using the x-axis, y-axis, z-axis. The coordinates of any point in three-dimensional geometry have three coordinates, (x, y, z).
The three-dimensional cartesian coordinate system consists of three axes, the x-axis, the y-axis, and the z-axis, which are mutually perpendicular to each other and have the same units of length across all three axes. Similar to the two-dimensional coordinate system, here also the point of intersection of these three axes is the origin O, and these axes divide the space into eight octants. Any point in 3D Geometry is represented with the coordinates (x, y, z).
Further the coordinates of a points in the eight octants are (+x,+y,+z), (-x,+y,+z), (+x,+y,-z), (-x,+y,-z), (+x,-y,+z), (-x,-y,+z), (+x,-y,-z), (-x,-y,-z).
Notation of a point in a cartesian coordinate system is a way of presenting a point for easy understanding and calculations. The points in a cartesian coordinate system are written in parentheses, and separated by a comma. The examples of a point in a three-dimensional frame is (2, 5, 4). The origin is denoted by the O and the coordinates of a point is denoted by the point (x, y, z). Here the last alphabets of the alphabetical series are taken or the first alphabets of the word is taken to represent the coordinates of a point.
A coordinate is an address, which helps to locate a point in space. For a three-dimensional frame, the coordinates of a point is (x, y, z). Here let us take note of these three important terms.
- Abscissa: It is the x value in the point (x, y, z) and is the distance of this point along the x-axis, from the origin
- Ordinate: It is the y value in the point (x, y, z) and is the perpendicular distance of the point from the x-axis, and is parallel to the y-axis.
- Applicate: In a three-dimensional frame the point is (x, y, z), and the z -coordinate of the point and is referred to as applicate.
Three Dimensional Geometry - Important Concepts
The 3D geometry makes use of the three coordinates to represent a point. The important concepts with reference to three-dimensional geometry are direction ratio, direction cosine, distance formula, midpoint formula, and section formula. The following are the important concepts of 3D Geometry.
Direction Ratios
The point A,(a, b, c) is represented as a vector with the position vector as → O A = a → i + b → j + c → k and has the direction ratios a, b, c. This ratio represents the vector line with reference to the x-axis, y-axis, and z-axis respectively. Further, these direction ratios also help to derive the direction cosines.
Direction Cosine
Direction Cosine gives the relation of a vector or a line in a three-dimensional space, with each of the three axes. The direction cosine is the cosine of the angle subtended by this line with the x-axis, y-axis, and z-axis respectively. If the angles subtended by the line with the three axes are α, β, and γ, then the direction cosines are Cosα, Cosβ, Cosγ respectively. 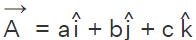 is
is 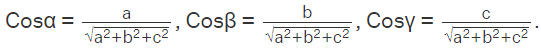 The direction cosines are also represented by l, m, n, and we can prove that l2 + m2 + n2 = 1.
The direction cosines are also represented by l, m, n, and we can prove that l2 + m2 + n2 = 1.
Distance Formula
The distance between two points (x1 , y1 , z1) and x2, y2, z2) is the shortest distance, and is equal to the square root of the summation of the square of the difference of the x coordinates, the y-coordinates, and the z-coordinates of the two given points. The formula for the distance between two points is as follows.
Mid-Point Formula
The formula to find the midpoint of the line joining the points (x1, y1, z1) and x2, y2, z2) is a new point, whose abscissa is the average of the x values of the two given points, and the ordinate is the average of the y values of the two given points. The midpoint lies on the line joining the two points and is located exactly between the two points.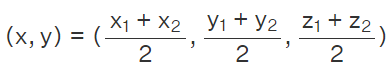
Section Formula
The section formula is useful to find the coordinates of a point that divides the line segment joining the points ( x1, y1, z1) and (x2, y2, z2) in the ratio m : n . The point dividing the given two points lies on the line joining the two points and is available either between the two points or on the line, beyond the two points.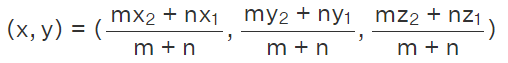
3D Geometry Representation of A Point, Line, Plane
The three dimensional geometry is used for the representation of a point, line, or a plane. Let us check the different forms of representation of a point, line, and plane in three-dimensional geometry.
Representation of a point in 3D Geometry
The point in a three-dimensional geometry can be represented either in cartesian form or a vector form. The two forms of representation of the point in a 3D geometry are as follows.
Cartesian Form: The cartesian form of representation of any point in 3D geometry uses three coordinates with reference to the x-axis, y-axis, and z-axis respectively. The coordinates of any point in a 3D geometry is (x, y, z). The x value of the point is called the abscissa, the y value is called the ordinate, and the z value is called the applicate.
Vector Form: The vector form of representation of a point P is a position vector OP, and is written as → O P = x → i + y → j + z → k , where → i , → j , → k are the unit vectors along the x-axis, y-axis, and z-axis respectively.
Representation of A Line in 3D Geometry
The equation of a line in a three-dimensional cartesian system can be computed from the following two methods. The two methods of finding the equation of a line are as follows.
- The equation of a line passing through a point 'a' and parallel to a given vector 'b' is as follows. r = a + λb
- The equation of a line passing through two given points, a and b, can be represented as r = a + λ(b - a)
Representation of A Plane in 3D Geometry
The equation of a plane in a cartesian coordinate system can be computed through different methods based on the available inputs values about the plane. The following are the four different expressions for the equation of a plane.
- Normal Form: Equation of a plane at a perpendicular distance d from the origin and having a unit normal vector
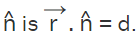
- Perpendicular to a given Line and through a Point: The equation of a plane perpendicular to a given vector
 and passing through a point
and passing through a point 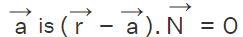
- Through three Non Collinear Lines: The equation of a plane passing through three non collinear points
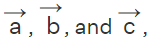 is
is 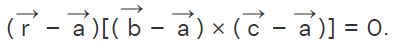
- Intersection of Two Planes: The equation of a plane passing through the intersection of two planes
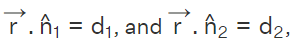 is
is 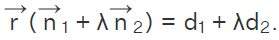
|
433 videos|220 docs|166 tests
|















