Time, Speed and Distance: Problems on Trains | General Test Preparation for CUET UG - CUET Commerce PDF Download
- Problems on trains are very common in competitive exams. Various types of questions are asked on trains.
- Questions on trains are solved using the concepts of time, speed and distance.
Given below is a list of some important points that need to be kept in mind while solving questions on trains.

Key Definitions
Speed: The rate at which an object covers distance, typically measured in km/h or m/s. It determines how quickly a train moves.
Distance: The total length covered by a train, such as its own length, the length of a platform, or the sum of two trains’ lengths when crossing.
Time: The duration taken to cover a distance or complete an event, like crossing a pole or another train, measured in hours or seconds.
Relative Speed: The effective speed of one object with respect to another. For two trains:
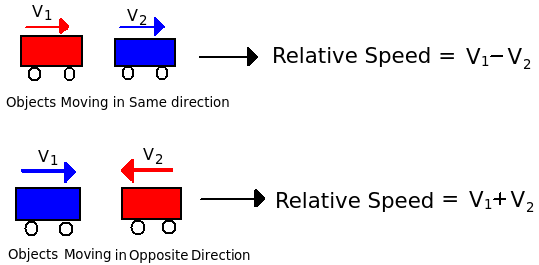
Same Direction: Relative speed = Speed of faster train - Speed of slower train.
Opposite Direction: Relative speed = Speed of Train A + Speed of Train B.
Downstream/Upstream Speed: For boats and streams, downstream speed is the boat’s speed plus the stream’s speed, while upstream speed is the boat’s speed minus the stream’s speed.
Note: Understanding these definitions is crucial for applying formulas correctly in train and boat problems.
Basic Formulas to Remember
- Speed = Distance / Time
- 1 km/hr = 5/18 m/s
- 1 m/s = 18/5 km/hr
- If the distance is same, then
Average Speed = 2AB/A+B- If a train of length 'L1' overtakes any other train or passes a platform of length 'L'2 . Then,
Distance Covered by the train = L1 + L2- If two trains with speed S1 & S2 respectively are moving in the same direction, their relative speed (Rs) will be
Rs = S1-S2- If two trains with speed S1 & S2 respectively are moving in the opposite direction, their relative speed (Rs) will be
Rs = S1+S2- In case of boats and streams, we generally take
x = Speed of boat in still water.
y = Speed of boat in stream.- Downstream speed (Ds) = x + y
Upstream Speed (Us) = x - y- On solving the above equations we can also find the values of x and y that are
x = (Ds + Us)/2
y = (Ds - Us)/2
where, Ds = Downstream Speed
Us = Upstream Speed- In Police - thief case,
Remember that
Speed of Police > Speed of thief (therefore he will be able to catch the thief)
Relative Speed
- “Relative” means “in comparison to”. Thus, the concept of relative Speed is used when two or more bodies moving with some Speed are considered.
- To make things simpler, one body can be made stationary (i.e. Speed =zero) and take the Speed of the other body with respect to the stationary body, which is the sum of the Speeds if the bodies are moving in the opposite direction and the difference if they are moving in the same direction.
- This Speed of the moving body with respect to the stationary body is called the Relative Speed.
Important Points
- Relative Speed of 2 bodies = Sum of their individual Speeds if they are moving in the opposite direction = Difference of their individual Speeds if they are moving in the same direction.
- When two trains are going in the same direction, then their relative speed is the difference between the two speeds.
- When two trains are moving in the opposite direction, then their relative speed is the sum of the two speeds.
- When a train crosses a stationary man/ pole/ lamp post/ sign post- in all these cases, the object which the train crosses is stationary and the distance travelled is the length of the train.
- When it crosses a platform/ bridge- in these cases, the object which the train crosses is stationary and the distance travelled is the length of the train and the length of the object.
- When a train crosses a car/ bicycle/ a mobile man- in these cases, the relative speed between the train and the object is taken depending upon the direction of the movement of the other object relative to the train- and the distance travelled is the length of the train.
Solved Examples: Relative Speed
Example 1: The thief Bhagu Ram is spotted by the policeman Pakad Singh from a Distance of 200m. Once they see each other they start running. What is the Distance Bhagu Ram who is running at 5 kmph would have covered before being caught by Pakad Singh running at 7 kmph?
Sol: Here are two bodies moving at different Speeds.
So assume Bhagu Ram to be stationary and take the Speed of Pakad Singh relative to Bhagu Ram.
So, now once the concept of relative Speed is applied, it can be deduced that Bhagu Ram is standing and Pakad Singh who is at a Distance of 200 m is running at 7 – 5 = 2 kmph.
To catch Bhagu Ram he needs to travel a Distance of 200 ms or 0.2 km.
So Time taken = 0.2/2 = 0.1 hours or 6 minutes.
Thus the Distance that is covered by Bhagu Ram before being caught is 0.5 km.
Example 2: A bird is sitting on a train A moving at a Speed of 40 kmph. It sees another train B at a Distance of 200 ms with Speed of 60 kmph coming from the opposite direction on the same rail track. It flies with an average Speed of 10kmph and sits on another train. Again immediately it flies back to the first train and again to the second train and so on. It does so before the two trains crash. What is the total Distance travelled by the bird?
Sol: Two trains are moving in opposite direction with Speed 40 kmph and 60 kmph.
Make train B stationary and then take the Speed of train A relative to the train B.
So relative Speed of train A = 40 + 60 = 100 kmph.
Before it crashes into the stationary train B it has to travel a Distance of 200 m which it will do in (0.2/100 ) hours.
During this duration, the average Speed of bird has been 10 kmph i.e. before the crash total Distance covered by the bird
= 0.2 * 10/100 km
=20 meters.
Some Specific Cases of Relative Speed
CASE 1 : Boats & Streams
- Let the Speed of the boat in still water = x and Speed of stream = y
- As it is previously discussed that in questions where two bodies with different Speeds are concerned, the concept of relative Speed should be used.
- Here, the stream can be assumed to be the stationary body, and the Speed of the boat relative to the Speed of the stream can be taken.
- Using the concept of relative Speed, one can now have the situation where the stream is stationary and only the boat is moving at a Speed determined by the direction of the boat relative to the stream.
- Therefore, the Downstream Speed of the boat (Ds) = x + y
and Upstream Speed of the boat (Us) = x - y - If Downstream Speed 'Ds' and Upstream Speed 'Us' are given, then
Speed of boat (x) = (Ds + Us)/2 ,
Speed of stream (y) = (Ds - Us)/2
Example 1: Gita rows a boat at a speed of 15 kmph upstream and 20 kmph downstream. Find the Speed with which Gita rows the boat in still water and also find the Speed of the stream.
Sol: Given that upstream Speed = 15 kmph
Downstream Speed = 20 kmph
Speed of Gita in still water = x = (Ds + Us)/2= (20+15)/2 = 35/2
Speed of stream =y = ( (Ds - Us)/2= (20-15)/2 = 5/2.
Example 2: The Speed of Narmada River is 5 kmph. A stationary body is placed in the river. Find the Time taken by the floating body to reach a stone which is 10 km downstream from the point where it is now?
Sol: Speed of body = Speed of river (as Speed of boy is 0) = 5 kmph
Speed=Distance/Time.
So, Time taken to reach 10 km = 10/5 = 2 hours.
Example 3: A man rows 135 km upstream in 2.7 hours. He rows the same Distance downstream in 2.5 hours. However, for downstream, he reduces his Speed by 9%, while the Speed of the current gets reduced by 20%. Find the Speed of the man.
(a) 52
(b) 55
(c) 50
(d) None of these
Ans: Option 'b' is correct.
Sol: Let us use a different approach for this question
x= The speed of boat and
y= The Speed of stream
Given that x-y= 135/2.7= 50 -—–(1)
Given that 10/11 x + 4/5 y = 135/2.5 = 54 ——–(2)
(reduction of 9% = 100- 9 = 0.91x. 0.91 in terms of a fraction can be written as 10/11 since 1/11= 0.0909).
(Similarly, reduction of 20% => 0.8 y. 0.8 in terms of a fraction can be written as 4/5.Go from answer options-
Option (c)The Speed of the man cannot be 50, as the Speed of the stream cannot be zero (on substituting in equation (1))option (b) substitute x= 52 and x=55 in the second equation and see for which value you are getting an integral value for y.
This happens only for x=55, where you will get y=5. Hence answer is the option
(b) Here the Reverse Gear approach is used i.e. working from answer options.
It should be remembered that longer the question, the easier it is to eliminate the wrong answer options.
CASE 2: A Moving Body and Stationary Body of Negligible Length
- Assume a stationary pole and a train approaching it.
- Here, the Speed of the train relative to the pole will be the Speed of the train itself, as the pole has a Speed of zero.
- Also, since the pole is of negligible length in comparison to the train, the Distance travelled by the train to pass the pole will be the length of the train itself.
- Hence, the Time taken by a train with length L1 and Speed S1 to pass a post/ stationary pole = L1/S1
Example: A train is travelling at a Speed of 4 m/s. Raman is standing on the road. How much Time will it take for the train to cross him if the length of the train is 200m?
Sol: Time taken to pass Raman= (Length of train)/(Speed of train)
= 200/4
= 50 sec.
CASE 3: A Moving Body and Stationary Body of Some Length
- Now let’s assume that the same train is going to pass a long bridge of length L.
The new distance covered by the train while passing over the bridge = the length of the bridge + the length of the train. - The speed of the train relative to the bridge will be the Speed of the train itself, as the bridge is stationary.
- The time taken by a train of length L1 and Speed S1 to pass a bridge of length L = (L1+ L)/S1.
Here, the Distance to be covered is the sum of the lengths of the train and the bridge.
CASE 4: Two Moving Bodies in Opposite Directions
- When two bodies move in opposite directions,
the Relative Speed = Sum of Speeds
Example: For a person sitting in a train moving with a Speed of 40 km/hr in the west direction, another train which is going towards east with a Speed of 40 km/hr, will appear to move at a Speed of?
Ans: (40+40) = 80 km/hr. - There are two trains with lengths L1 and L2 and speeds S1 and S2, respectively, moving in the opposite direction.
Time taken by the trains to cross each other after meeting = (L1+L2)/(S1+ S2 ) - Here, the total distance to be covered is the sum of the lengths of the trains, and the relative speed is the sum of the Speeds (since they are moving in the opposite direction).
CASE 5: Two Moving Bodies in the Same Direction
- When two bodies move in the same direction,
then the Relative Speed = the Difference of Speeds
Example: For a person sitting in a train moving with a Speed of 60 km/hr in the west direction, another train which is going towards the west with a Speed of 40 km/hr, will appear to move at a Speed of?
Ans: (60-40) = 20 km/hr. - There are two trains of lengths L1 and L2 and travelling at Speeds S1 and S2, respectively, moving in the same direction.
Time taken by the trains to cross each other after meeting = (L1+L2)/(S1 – S2 ) - Here, the Total Distance to be covered is the sum of the lengths of the trains, and the relative speed is the difference between the speeds (since they are moving in the opposite direction).
Example1: Train A, which is 125 m long, is travelling at 108 km/hr. On a parallel track, a 180 m long Train B is travelling at 72 km/hr, in the same direction. In Train B, a passenger is walking towards the rear end of the train at a Speed of 9 km/hr. In how many seconds will Train A completely cross the passenger in Train B
(a) 14.4
(b) 10
(c) 16.67
(d) 24
Ans: Option 'b' is correct
Sol: Speed of A = 108 km/hr = 30 m/s
Speed of train B = 72 km/hr = 20 m/s
Here r the relative Speed between train A and train B should be considered first i.e.= 30 -20 = 10 m/s.
Relative Speed -Train A and man moving in the opposite direction with a Speed of 2.5 m/s=10 +2.5 = 12.5m/s
Time taken by train A to pass the man who is moving in the opposite direction = 125/12.5 = 10 secs since the Distance to be covered over here is the length of train A only.
Example 2: How much Time a 100m long train travelling at a Speed of 8 m/s will take to overtake another train which is 80m and is travelling in the same direction at a Speed of 4 m/s?
Sol: Suppose the 80 m long train is stationary and take the Speed of the 100m long train in relative to the former.
So relative Speed of 100m long train = 8 – 4 = 4 m/s.
To overtake the 80m long train it has to travel a total Distance = sum of its own length and that of the other train = 100 m + 80 m = 180 m
So to travel that Distance with a Speed of 4 m/s, it will take 180/4= 45 secs.
Solved Questions: Trains
Q 1: A train travelling at 60 kmph crosses a man in 6 seconds. What is the length of the train?
Sol: Speed in m/sec = 60 *(5/18) = 50/3 m/sec
Time taken to cross the man = 6 secs
Therefore, Distance = (50/3)* 6 = 100 meter (i.e. the length of the train)
Q 2: A train travelling at 60 kmph crosses another train travelling in the same direction at 50 kmph in 30 seconds. What is the combined length of both trains?
Sol: Speed of train A = 60 kmph = 60* (5/18) = 50/3 m/sec
Speed of train B = = 50 kmph = 50 *(5/18) = 125/9 m/sec
The relative speed =(50/3)-(125/9)=25/9 m/s (we have subtracted the two values because
both the trains are going in the same direction)
Time taken by train A to cross train B = 30 secs
Distance = Speed * Time
Distance =25/9 * 30 = 250/3 meter (i.e. the combined length of both trains)
Q 3: Train A, 600 mts long is running at 80 kmph will take how much time to cross a man sitting in another train, which is 400 m long, running at 64 kmph in the opposite direction?
Sol: Distance = 600 meters
Total Speed = 64 + 80 = 144 kmph (added because they are travelling in opposite directions)
In m/sec, speed = 144 *(5/18) = 40 m/sec
Distance = Speed x Time
600 = 40 x Time
Therefore, Time = 15 seconds
Q 4: Two trains start at the same time from Pune and Delhi and proceed towards each other at 80 kmph and 95 kmph respectively. When they meet, it is found that one train has travelled 180 km more than the other. Find the distance between Delhi and Pune.
Sol: Let t be the time after they meet
Distance1 = Speed * Time = 80 * t = 80t
Distance2 = Speed * Time = 95 * t = 95t
As the distance gap between both trains is 180 kms
Therefore, we can say that:
95t - 80t = 180
15t = 180
t = 12 seconds
Total Distance, (95+80) t = 175 * 12 (t = 12)
Distance = 2100 kms
Q 5: The distance between two places A and B is 570 kms. A train starts from A at 50 kmph at 6 am and another starts from B at 80 kmph at 7 am towards each other. At what time will they meet?
Sol: Let the two trains meet at a distance x km from place A
Time required by the train starting from A to cover x is x/50 hr
Time taken by the other train starting from B to cover (570 - x) km = (570-x)/80
But the first train has started 1 hr early. So, it has travelled 50 km in this 1 hr.
Therefore, x/50 - 1= (570-x)/80
On Solving, x = 250
So, they will meet at a distance of 250 km from place A
So the time at which they will meet will be (250/50) = 5 hrs (after 6 am)
Hence, they will meet at 11 am.
Q 6: The average speed of a train without stoppages is 48 kmph and average speed with stoppages is 40 kmph. How many minutes in an hour the train stops on an average.
Sol: If the train were to travel without stoppages, it would cover 48 km.
With stoppages, the average speed reduces by (48-40) = 8 km
Therefore, (8/48)* 60 minutes = 10 minutes
Hence, 10 minutes would be the time per hour the train stops on an average.
Q 7: Indrayani Express leaves Pune for Bombay at 17:30 hrs and reaches Bombay at 21:30 hrs. While, Shatabdi, which leaves Bombay at 17:00 hrs reaches Pune at 20:30 hrs. At what time do they pass each other
Sol: Let the distance between Bombay and Pune = d km
Indrayani’s Speed =(d/4) kmph and that of Shatabdi = (d/3.5)kmph
Let t be the time in hrs after Shatabdi has left for Pune, when the two trains meet
Therefore, distance travelled by Shatabdi = (d/3.5)* t
And that of Indrayani =(d/4) * (t-30/60)
The sum of the distances travelled by the two trains = distance between Bombay and Pune = d km
Therefore, (d/3.5)* t +(d/4) * (t-30/60)=d
Solving for t, we get t = 2.1 hrs or 2 hrs and 6 mins
Hence, the two trains meet at 19:06 hrs
Q 8: How long will a 150 m long train running at a speed of 60 kmph take to cross a bridge of 300 m?
Sol: Total Distance = 300 + 150 = 450 m
Speed = 60 kmph = 60 *(5/18)=(50/3) m/sec
Distance = Speed * Time
450 =(50/3) * Time
Time = 27 seconds
Preparation Strategy for Train Problems
To master train-related problems, follow this structured approach:
Understand Core Concepts: Memorise key formulas (e.g., relative speed, distance = speed × time) and their applications. Focus on relative speed for the same and opposite directions.
Practice Variety: Solve at least 5–10 problems daily, covering stationary objects (poles, platforms), moving objects (trains, people), and boats/streams.
Time Management: Aim to solve each problem in 1–2 minutes, simulating exam conditions.
Analyse Mistakes: Review incorrect solutions to identify conceptual gaps.
Mock Tests: Take weekly mock tests to build speed and accuracy.
Revise Regularly: Maintain a formula sheet and revisit weak topics (e.g., boats and streams) weekly.
EduRev Tip: Dedicate 30–45 minutes daily to train problems, balancing with other Quantitative Aptitude topics.
Common Mistakes in Train Problems and Solutions
Mistake: Confusing relative speed for same vs. opposite directions.
Solution: Always subtract speeds for the same direction (S₁ - S₂) and add for opposite (S₁ + S₂). Double-check problem wording.Mistake: Ignoring unit conversions (km/h to m/s or vice versa).
Solution: Convert speeds to m/s when distances are in meters (use 5/18 multiplier). Verify units before calculations.Mistake: Incorrect distance for crossing scenarios.
Solution: Use the length of the train for stationary poles/people; sum of lengths for platforms or two trains. Create a checklist for distance components.Mistake: Neglecting time differences in meeting problems.
Solution: Account for start time gaps by adjusting distances or using relative time equations.Mistake: Rushing without verifying answers.
Solution: Recalculate using alternative methods (e.g., reverse gear approach) or check if the answer fits all conditions.
|
201 videos|1014 docs|2272 tests
|
FAQs on Time, Speed and Distance: Problems on Trains - General Test Preparation for CUET UG - CUET Commerce
| 1. What is the formula for calculating relative speed when two trains are moving in the same direction? |  |
| 2. How do you calculate the time taken for a train to cross a stationary pole? |  |
| 3. If two trains are moving towards each other, how do you find their relative speed? |  |
| 4. What factors affect the time taken for two trains to cross each other? |  |
| 5. Can the concept of relative speed be applied to objects other than trains? |  |

















